
- •1. ЭЛЕМЕНТЫ ЛИНЕЙНОЙ АЛГЕБРЫ
- •1.2. Правило вычисления определителя любого порядка
- •1.4. Математические операции над матрицами
- •1.5. Понятие системы линейных алгебраических уравнений
- •1.6. Решение систем линейных алгебраических уравнений
- •2. ВЕКТОРНАЯ АЛГЕБРА
- •2.3. Линейные операции над векторами
- •2.6. Векторное произведение векторов
- •2.7. Понятие смешанного произведения векторов
- •3. АНАЛИТИЧЕСКАЯ ГЕОМЕТРИЯ
- •3.1. Линия на плоскости
- •3.2.4. Прямая, проходящая через две заданные точки
- •3.2.7. Расстояние от точки до прямой
- •3.2.8. Деление отрезка в данном отношении λ
- •3.3. Кривые второго порядка
- •3.3.1. Окружность
- •3.3.2. Эллипс
- •3.3.3. Гипербола
- •3.3.4. Парабола
- •3.3.5. Общее уравнение кривой второго порядка
- •3.4. Плоскость в пространстве
- •3.4.1. Общее уравнение плоскости
- •3.4.2. Неполные уравнения плоскости
- •3.4.5. Взаимное расположение двух плоскостей в пространстве
- •3.5.2. Канонические уравнения прямой
- •3.5.3. Параметрические уравнения прямой
- •3.5.6. Взаимное расположение прямой и плоскости
- •4. МАТЕМАТИЧЕСКИЙ АНАЛИЗ
- •4.1. Основные понятия
- •4.2. Классификация основных элементарных функций
- •4.3. Предел функции
- •4.6. Основные свойства конечных пределов
- •4.7. Вычисление пределов
- •4.8.4. Свойства функции, непрерывной на отрезке
- •4.9.7. Правило Лопиталя
- •4.10.2. Интервалы монотонности функции. Точки экстремума
- •4.10.5. Четность, нечетность и периодичность функции
- •4.10.6. Нули функции и дополнительные точки
- •Вопросы для самопроверки
Скалярный квадрат вектора равен квадрату его модуля.
Тогда i i 1; |
j j 1; |
k k 1 . Если |
|
|
и наоборот. |
a |
b , то a b 0 |
||||
|
|
|
|
|
|
Следовательно, условие перпендикулярности векторов: a b a b 0 . |
|||||
Тогда i j 0 ; |
i k 0 ; |
j k 0 . |
|
|
|
Найдем скалярное произведение векторов, заданных в координатной форме.
Пусть |
|
|
;az axi ay |
j az k , |
b bx ;by ;bz bxi by j bz k , тогда |
a ax ;ay |
|||||
|
|
|
|
|
|
a b |
axi ay j azk bxi by j bzk axbx ayby azbz . |
||||
Скалярное произведение в координатной форме равно сумме парных произведений одноименных координат векторов.
Физический смысл скалярного произведения: A F S F S cos . Работа
постоянной силы F на прямолинейном пути S равна скалярному произведению вектора силы F на вектор перемещения S .
Примеры .
|
3 j k и |
b 1; 2; |
2 , |
1) Найти скалярное произведение векторов a 2i |
угол между ними, проекцию одного вектора на другой.
2)Найти работу силы F 3; 1; 1 на прямолинейном пути S i j 2k .
2.6.Векторное произведение векторов
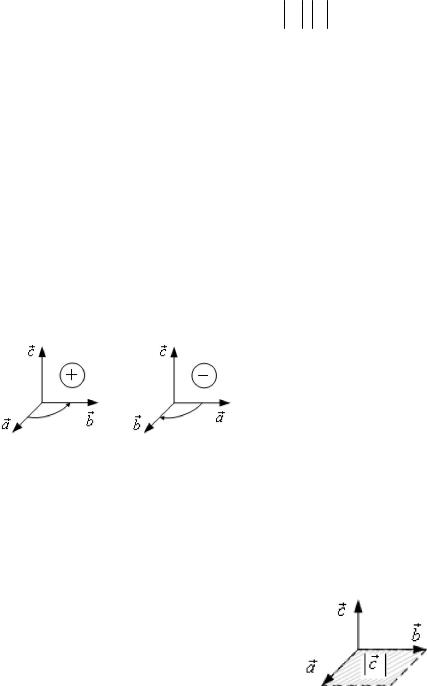
Определение. Тройка некомпланарных векторов a, b , c называется пра-
вой (+), если кратчайший поворот от a к b из конца оси c виден против часовой стрелки, в противном случае, тройка называется левой (–).
Рис. 2.11
Координатные орты ( i , j , k ) составляют правую тройку векторов, система
координат в этом случае называется тоже правой.
Определение . Векторным произведением a на b называется вектор c ,
|
|
|
|
|
|
|
|
|
|
|
|
|
и удовлетворяющий условиям: |
обозначаемый символом c |
a b |
||||||||||||
1) |
|
|
|
|
|
|
|
|
b |
|
sin , φ – угол между a и b ; |
||
|
|
|
|
|
|
||||||||
|
|
|
|
||||||||||
|
c |
|
|
a |
|
|
|
||||||
2) |
c |
|
|
|
|
|
|
|
|
|
|||
a , c b ; |
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
3) тройка векторов a, b , c образует правую тройку.
Рис.2.12
21
Геометрический смысл |
|
|
|
: |
Модуль векторного произведения |
|
|
|
|
|||||
|
|
|
|
|||||||||||
|
a b |
|
|
a b |
|
|
||||||||
численно равен площади параллелограмма, построенного на векторах a , |
|
b , как |
||||||||||||
на сторонах. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Следствие. Площадь треугольника, построенного на векторах a , b , как на |
||||||||||||||
сторонах, равна половине модуля векторного произведения a на b , S |
1 |
|
|
|
|
|
. |
|||||||
|
|
|
||||||||||||
2 |
|
a b |
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
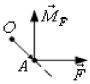
Момент силы F , приложенной к т. А, относи- |
|||||||||||||
Физический смысл a b : |
|
|||||||||||||
тельно т.О равен векторному произведению вектора OA на вектор силы F , |
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
M F OA F M xi M y j M zk . Тройка (OA, F , M F ) должна |
|
|
|
|
|
|
|
|
|
|||||
быть правой. Координаты M x , M y , M z |
вектора M F есть моменты |
|
|
|
|
|
|
|
|
|
||||
этой силы относительно координатных осей. |
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
Рис. 2.13 |
|||||||||
Свойства a b :
1)a b b a (антикоммутативность);
2)1a 2b 1 2a b ;
|
|
|
|
|
3) c |
a |
b c |
a |
c b . |
Таким образом, векторные многочлены можно перемножать векторно по правилу перемножения алгебраических многочленов, учитывая антикоммутативность.
Пусть a axi ay j azk , b bxi by j bzk . Найдем векторное произведе-
ние ортов: i i 0 , |
т. к. |
i i |
|
|
i |
|
i |
|
sin0 0 ; аналогично |
j j 0 , k k 0 ; |
||||||||||||
i j k , действительно, |
i k , |
|
j k , |
|
|
|
|
|
|
sin |
|
|
|
|
|
|||||||
|
k |
i |
|
|
j |
1 и тройка i , j ,k – пра- |
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
вая. Аналогично можно получить |
j k i |
и т. д. |
|
|
|
|
||||||||||||||||
|
|
|
|
|
||||||||||||||||||
Объединим всевозможные векторные произведения ортов i , j , k |
в таблицу: |
|||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
i j k i |
j k |
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
. |
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
Тогда a b axi ay j azk bxi by j bzk |
|
|
|
|
|
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
k |
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
i |
j |
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
ax |
ay |
az |
. |
|
|
||||||
i aybz azby j axbz bxaz k |
axby bxay |
|
|
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
bx |
by |
bz |
|
|
|
||||
Примеры . |
|
|
|
|
, если a 1; 2; |
2 ; |
b i k . |
|
||||||||||||||
1. Найти 2a |
3b |
|
||||||||||||||||||||
2. Найти S ABC , т. А(1; -1), т.В(4; -2), т.С(3;3). |
|
|
|
|
|
|||||||||||||||||
2.7. Понятие смешанного произведения векторов |
|
|
||||||||||||||||||||
Определение. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Смешанным произведением векторов a, b , c называется ска- |
||||||||||||||||||||||
лярное произведение вектора |
|
|
|
|
на вектор c . |
|
|
|
|
|
||||||||||||
a b |
|
|
|
|
|
|
||||||||||||||||
22
