6.2 Поняття ідеального газу та його закони

Ідеальний – це газ, в якому нехтують власним об’ємом молекул і силами взаємодії між ними.

Стан газу характеризується такими величинами: m – маса, P – тиск, V – об’єм, T – абсолютна температура. Закони ідеального газу встановлюють зв’язок між цими параметрами.

Ізотермічний закон (закон Бойля-Маріотта) m = const, T= const: при незмінній масі і температурі добуток тиску на об’єм залишається незмінним

. (6.1)

Г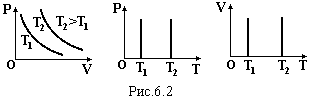рафіки цього закону зображені на рис.6.2 в різних координатах.

Ізобарний закон (закон Гей-Люсака) m = const, P = const: при незмінній масі і тискові об’єм газу прямо пропорційний температурі

. (6.2)

Тут V_o – об’єм газу при температурі 0^оС, - температурний коефіцієнт об’ємного розширення. Він показує відносну зміну об’єму при зміні температури на 1⁰. Вимірюється в 1/град, і для всіх ідеальних газів величина однакова і дорівнює 1/273 (1/град). Тому (6.2) набуває виду

,

де Т=273+t^o – температура по абсолютній шкалі (шкала Кельвіна). Графіки цього закону зображені на рис.6.3.

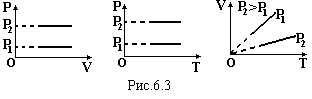
Ізохорний процес (закон Шарля) m = const, V = const: при незмінній масі і об’ємові тиск газу прямо пропорційний температурі

. (6.3)

Тут Р_o – об’єм газу при температурі 0^оС, - температурний коефіцієнт тиску. Він показує відносну зміну тиску при зміні температури на 1⁰. Вимірюється в 1/град, і для всіх ідеальних газів величина однакова і дорівнює 1/273 (1/град). Тому (6.3) набуває виду

. (6.4)

Графіки цього закону зображені на рис.6.4.

Зв’язок між усіма чотирма параметрами дає рівняння стану ідеального газу – рівняння Клапейрона-Менделєєва:

. (6.5)

Тут μ – молярна маса газу, R = 8,31 Дж/(моль∙К) – газова стала.

6.3 Закон Дальтона. Рівняння стану для суміші газів

Англійський фізик Дж. Дальтон (1766-1844) 1801-1803 р. експериментально встановив закон, який носить його ім’я (закон Дальтона): загальний тиск суміші хімічно не взаємодіючих газів дорівнює сумі парціальних тисків. Парціальний тиск – це тиск кожного газу, який встановлюється, коли в посудині знаходиться тільки цей газ, а інші відкачані.

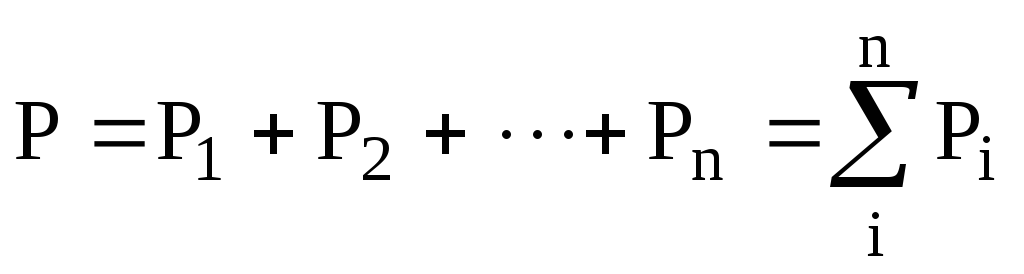. (6.6)

Одержимо рівняння стану для суміші газів. Запишемо із рівняння Клапейрона-Менделєєва (6.5) парціальні тиски:

, ,...,.

Загальний тиск знайдемо по закону (6.6) Дальтона

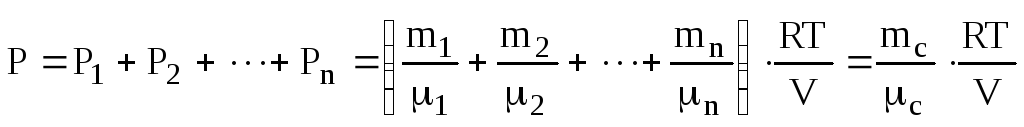, (6.7)

де молярна маса суміші газів 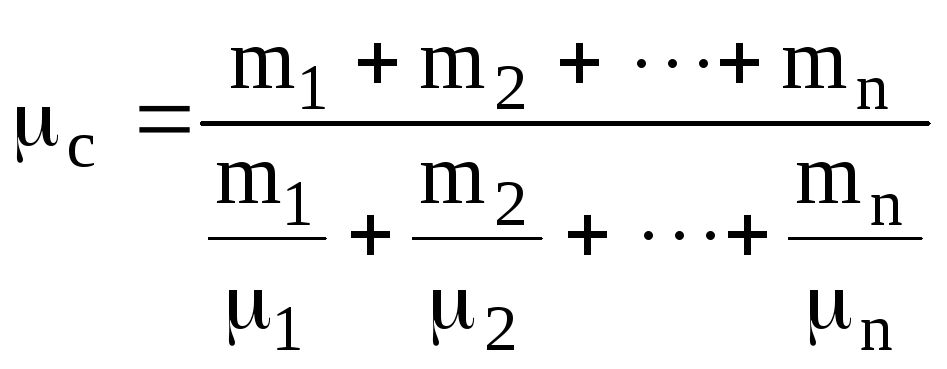(6.8)

Таким чином рівняння стану для суміші має такий же вид, як і (6.5) для одного газу, якщо замінити масу і молярну масу значеннями для суміші

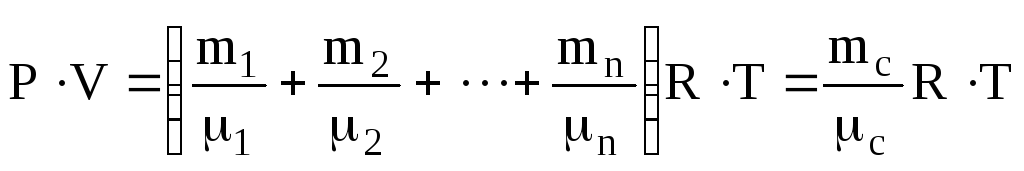. (6.9)

6.4 Основне рівняння молекулярно-кінетичної теорії

Основним рівнянням молекулярно-кінетичної теорії називається рівняння, яке дає зв’язок між тиском газу і енергією поступального руху молекул. Знайдемо це рівняння в таких припущеннях:

а) всі молекули рухаються з однаковими швидкостями;

б) так як рух молекул хаотичний, то всі напрямки руху рівно ймовірні, тобто можна вважати, що вздовж будь-якого напрям рухється однакова кількість молекул. Тому припустимо, що молекули рухаються тільки вздовж координатних осей х, y, z. Тоді можна вважати, що вздовж кожної осі рухається 1/3 частина всіх молекул.

Тиск газу пояснюється зміною імпульсу молекул при зіткненні і відбиванні їх із стінкою посудини. У відповідності з другим законом Ньютона на молекулу з боку стінки діє сила, а згідно з третім законом Ньютона, на стінку з боку молекули буде діяти така ж за величиною сила. Відношення сили до площі і є тиск.

В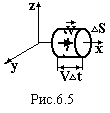иберемо на поверхні посудини малу плоску площадку ∆S. Вісь ох направимо перпендикулярно до цієї площадки, осі оy і oz паралельні їй (рис.6.5). Знайдемо кількість молекул ∆N, які за час ∆t зіткнуться з цією площадкою. Це будуть молекули, які рухаються до площадки, а це половина тих молекул, які рухаються вздовж осі ох, і віддалені від неї на відстань, не більшу ніж V∙∆t. . При пружному ударі імпульс молекули змінюється на 2mV. Якщо удар не пружний, тобто молекула прилипає до поверхні, то імпульс зміниться на mV. Але після встановлення динамічної рівноваги, кількість молекул, які прилипають до стінки і які її покидають стають однаковими. Молекула, покидаючи стінку, передає їй імпульс mV. Таким чином і в цьому випадку загальна зміна імпульсу теж буде дорівнювати 2mV, тобто немає різниці, та ж молекула покинула стінку, чи інша. Запишемо другий закон Ньютона і знайдемо тиск 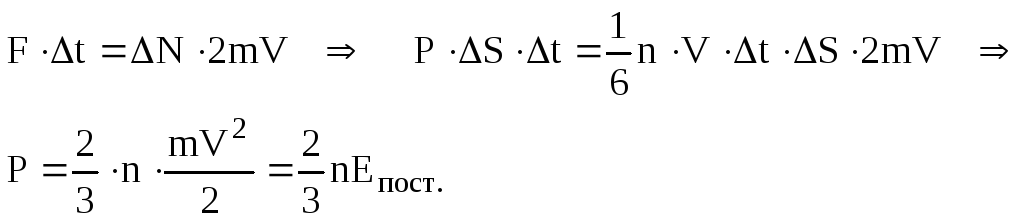(6.10) Реально швидкості молекул різні. Розбивши всі молекули на групи з однаковими швидкостями, парціальний тиск кожної групи молекул знаходиться по формулі (6.10). Скориставшись законом Дальтона, знайдемо загальний тиск

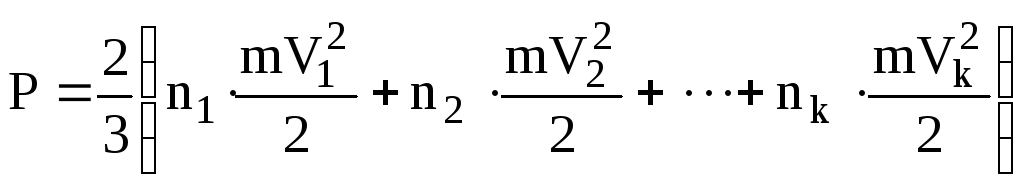. У дужках записана загальна енергія поступального руху всіх молекул. Її можна знайти ще як добуток концентрації молекул n на середню енергію поступального руху , де середня квадратична швидкість – це корінь квадратний із середнього значення квадратів швидкостей усіх N молекул (риска зверху означає середнє значення)

. (6.11)

Таким чином, основне рівняння молекулярно-кінетичної теорії має вид

. (6.12)