3.9 Сили в неінерціальних системах відліку. Сили інерції

Неінерціальними називаються системи, які рухаються з прискоренням відносно інерціальних систем. Закони Ньютона, на основі яких вивчається рух тіл, справедливі тільки для інерціальних систем. Щоб розширити можливість застосування математичного апарату вивчення руху тіл в інерціальних системах (див. розд. 3.3) до неінерціальних, вводяться особливі сили, сили інерції, виникнення яких зумовлене неінерціальним характером систем, а не взаємодією тіл, або полів.

Розрізняють неінерціальні системи, які рухаються відносно інерціальних поступально, і системи, що обертаються, навіть і рівномірно, так як при цьому виникає доцентрове (нормальне) прискорення.

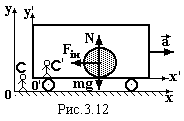
Розглянемо спочатку сили інерції в системах, які рухаються поступально з певним прискоренням. Нехай в інерціальній системі С може поступально з прискоренням рухатись вагон, з яким зв’язана неінерціальна система С^I. на горизонтальній підлозі вагона без тертя лежить куля масою m (рис.3.12). Коли вагон не рухається, обидві системи інерціальні. Спостерігачі С і С^I пояснюють рівновагу кулі першим законом Ньютона, тобто тим, що рівнодіюча сил тяжіння mg і сили N реакції підлоги дорівнює нулю.

Коли вагон рухається з прискоренням, поводження кулі для спостерігачів різне. Спостерігач С бачить, що вагон рухається, а куля, із-за відсутності тертя залишається в його системі нерухомою знову таки у відповідності з першим законом Ньютона.

Спостерігач С^I бачить, що дія сторонніх сил на кулю не змінилась, але вона почала рухатись на нього з прискоренням

Тоді він робить закономірний висновок, що на кулю почала діяти деяка сила, яка і надає кулі цього прискорення. Причому поява цієї сили викликана не дією на кулю якихось інших тіл, а є результатом неінерціального характеру системи С^I. Ця сила називається силою інерції і дорівнює . (3.19)

Таким чином, в неінерціальних системах на тіла окрім ньютонівських сил діють іще й сили інерції. Тому другий закон Ньютона в цих системах відліку записується так

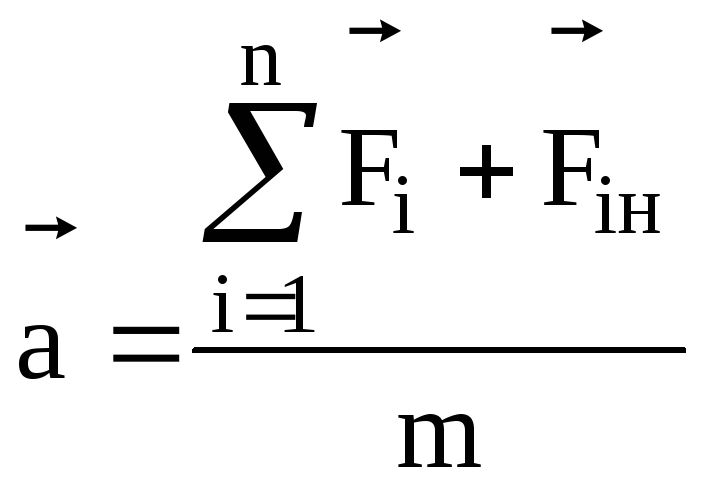. (3.20)

Приклад. До стелі ліфта підвішений вантаж масою m. Ліфт опускається вертикально вниз з прискоренням . Знайти силу натягу нитки.

Розв’язок в інерціальній системі спостерігачем С.

Другий закон Ньютона в скалярній формі в проекції на вертикальну вісь має вид

.

Розв’язок в неінерціальній системі спостерігачем С^I.

В його неінерціальній системі тіло знаходиться у стані спокою. Умова рівноваги має вид . Величина сили інерції, а її напрямок уже врахований в попередньому рівнянні. Маємотаку ж відповідь.

В системах, що обертаються, завжди виникає нормальне (доцентрове) прискорення . Тому виникає сила інерції, направлена проти цього прискорення, тобто від центра кривизни. Ця сила інерції називається відцентровою (Fв.ц.) і дорівнює, як і в поступальних системах . (3.21)

Наряду з цією силою інерції в обертальних системах виникає іще одна сила інерції – коріолісова сила, названа в честь французького фізика Г.Г.Коріоліса (1792-1843), який вперше її одержав теоретично. Вона виникає тоді, коли відносна швидкість тіла відмінна від нуля. З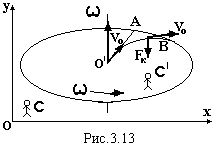’ясуємо напрямок цієї сили. Нехай в системі, яка обертається з кутовою швидкістю ω, вздовж радіуса без тертя рухається куля з відносною швидкістюV_o (рис.3.13). В інерціальній системі спостерігач С буде бачити рух кулі по прямій ОА. Диск же обертається, не впливаючи на рух кулі із-за відсутності тертя. Спостерігач С^I буде бачити рух кулі по дузі ОВ. Тому він робить правомірний висновок, що на кулю діє сила F_k перпендикулярна до швидкості, яка і змінює її напрямок. Це і є сила інерції Коріоліса. Вона перпендикулярна до векторів ω і V_o і дорівнює

. (3.22)

Таким чином, другий закон Ньютона записується в самому загальному випадку неінерціальних систем так:

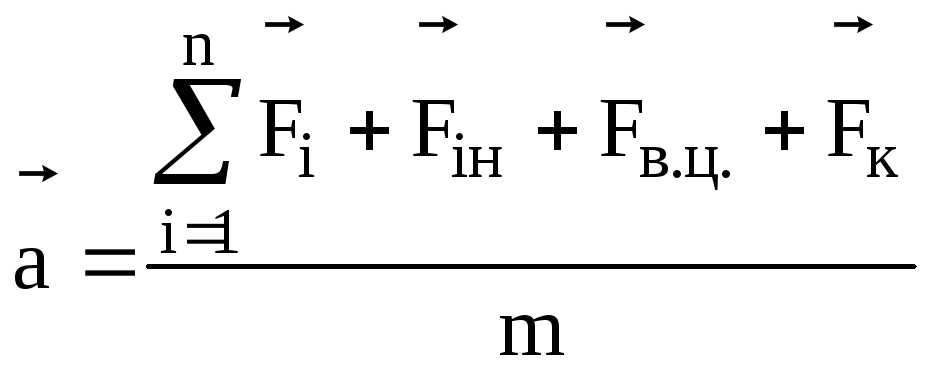. (3.23)