18. Степенной ряд. Теорема Абеля.

Важным случаем функциональных рядов являются степенные ряды:

(13)

или

Для выяснения свойств степенных рядов достаточно ограничиться рассмотрением рядов вида (13), так как ряд по степеням легко свести к виду (13) заменой переменных, т.е. переносом начала координат в точку

Для выяснения характера области сходимости степенного ряда сформулируем следующую теорему:

Теорема 6.1. (Абеля):

Пусть степенной ряд (13) сходится в точке Тогда он сходится абсолютно в любой точке х, для которойи равномерно в любой области.

Если степенной ряд (13) расходится в точке то он расходится и во всех точкахтаких, что.

Для определения области сходимости степенного ряда используется либо признак Даламбера, либо признак Коши.

Рассмотрим степенной ряд:

. (14)

Вычислим предел:

.(15)

Если существует предел (15), то ряд (14) сходится, если , и расходится, если. Следовательно, ряд (14) сходится абсолютно, если

,

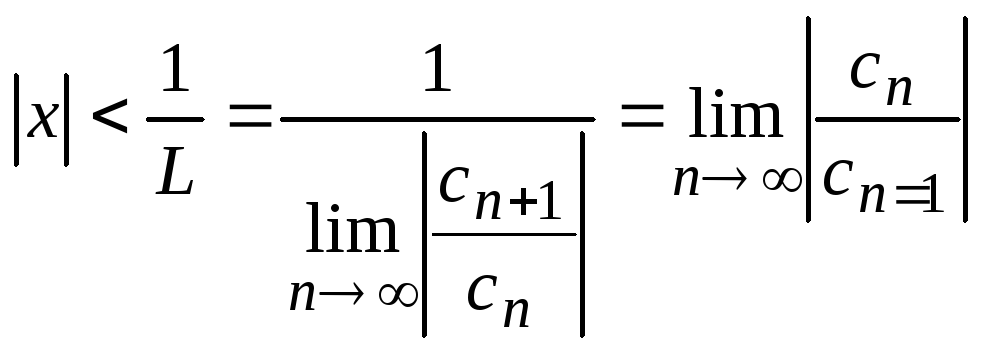и расходится, если

.

Определение:

Число , такое, что для всех x, удовлетворяющих условиюряд (13) сходится, а для всех х удовлетворяющих условиюряд расходится, называется радиусом сходимости ряда.

Формула для радиуса сходимости, получаемая с помощью признака Даламбера, имеет вид

(16)

Область сходимости ряда - так называют множество точек сходимости функционального ряда, т.е. множество значений аргумента х, для которых ряд (бесконечная сумма) сходится

Пример 6.1.

Найти область сходимости ряда Область сходимости ряда

при .

По признаку Даламбера:

что означает, что ряд сходится на всей оси Х.

19. Радиус сходимости степенного ряда. Формула Коши-Адамара для радиуса сходимости степенного ряда.

1) Степенной ряд сходится абсолютно на некотором интервале . Иными словами, если мы выбираем  любое значение «икс» из интервалаи подставляем его в общий член степенного ряда, то у нас получается абсолютно сходящийся числовой ряд. Такой интервали называется интервалом сходимости степенного ряда.

Радиус сходимости, если совсем просто, это половина длины интервала сходимости:

2) Степенной ряд сходится абсолютно при любом значении . То есть, какое бы значение «икс» мы не подставили в общий член степенного ряда – в любом случае у нас получится абсолютно сходящийся числовой ряд. Интервал сходимости и область сходимости в данном случае совпадают:. Радиус сходимости:. Рисунок приводить не буду, думаю, нет необходимости.

3) Степенной ряд сходится в единственной точке. Если ряд имеет вид , то он будет сходиться в единственной точке. В этом случае интервал сходимости и область сходимости ряда тоже совпадают и равны единственному числу – нулю:. Если ряд имеет вид, то он будет сходиться в единственной точке, если ряд имеет вид, то, понятно, – в точке «минус а». Радиус сходимости ряда во всех случаях, естественно, нулевой:

Радиус сходимости степенного ряда определяется по формуле Коши-Адамара

Здесь — верхний предел последовательности. Он всегда существует (конечный или бесконечный), и притом единственный. В случаеполагают, а в случаеполагают.

20. Ряд Тейлора. Теорема Тейлора о разложимости функции в ряд Тейлора. Разложение основных элементарных функций в ряд Тейлора-Маклорена: e^x, sinx, cosx, (1+x)^a, ln(1+x).

Пусть функция бесконечно дифференцируема в некоторой окрестности точки. Формальный ряд

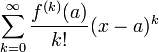
называется рядом Тейлора функции в точке.

В случае, если , этот ряд также называется рядом Маклорена.

Пусть . Тогда рядназывается рядом Тейлора функциив точке.

Если , топо формуле Тейлора:

, где - остаточный член формулы Тейлора, т.е., где- n-ая частичная сумма ряда Тейлора функциив точке.ряд Тейлора сходится натогда и только тогда, когда

Пусть и, тогда на

Доказательство: 

, где - остаточный член формулы Тейлора в форме Лагранжа:

.

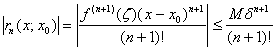Рассмотрим ряд ,по признаку Даламбера ряд сходится. Перейдем к пределу прив неравенстве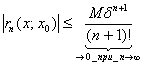на.

Теорема Тейлора

Пусть функция f(x) имеет в точке х = а и некоторой ее окрестности производные порядка до (n+1) включительно.{ Т.е. и все предыдущие до порядка n функции и их производные непрерывны и дифференцируемы в этой окрестности}.

2) Пусть х- любое значение из этой окрестности, но а  х Тогда между точками х и а найдется такая точка , что справедлива формула: это выражение называется формулой Тейлора, а выражение:называется остаточным членом в форме Лагранжа. Доказательство. Представим функцию f(x) в виде некоторого многочлена Pn(x), значение которого в точке х = а равно значению функции f(x), а значения его производных равно значениям соответствующих производных функции в точке х = а.(1) Многочлен Pn(x) будет близок к функции f(x). Чем больше значение n, тем ближе значения многочлена к значениям функции, тем точнее он повторяет функцию. Представим этот многочлен с неопределенными пока коэффициентами:(2) Для нахождения неопределенных коэффициентов вычисляем производные многочлена в точке х = а и составляем систему уравнений: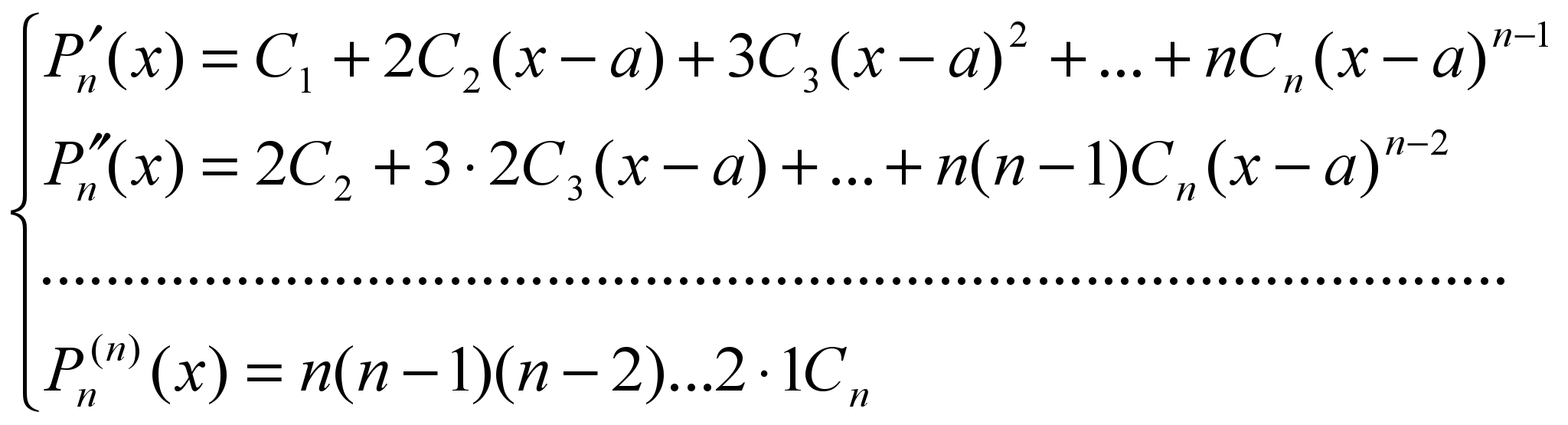(3) Решение этой системы при х = а не вызывает затруднений, получаем:…………………….Подставляя полученные значения Ci в формулу (2), получаем:Как было замечено выше, многочлен не точно совпадает с функцией f(x), т.е. отличается от нее на некоторую величину. Обозначим эту величину Rn+1(x). Тогда:

f(x) = Pn(x) + Rn+1(x) Теорема доказана.

  

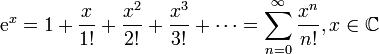
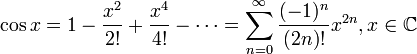
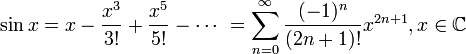
для всех

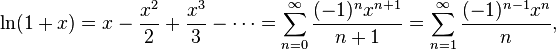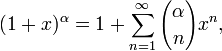для всех

для всех и всех комплексныхгде