
- •1*. Определенный интеграл. Интегральная сумма. Верхняя и нижняя интегральные суммы. Их свойства.
- •2**. Ограниченность интегрируемой функции.
- •3**(-). Критерий интегрируемости ограниченной на отрезке функции.
- •4≠. Теорема об интегрируемости монотонной на отрезке, а также непрерывной на отрезке функций.
- •5*. Основные свойства определенного интеграла.
- •6*. Формула среднего значения для определенного интеграла.
- •7. Интеграл с переменным верхним пределом. Его непрерывность и дифференцируемость.
- •8. Формула Ньютона-Лейбница для определенного интеграла.
- •9. Вычисление определенного интеграла по частям и заменой переменной.
- •10. Применение определенного интеграла (площадь плоской фигуры, длина дуги кривой, объем тела вращения).
- •11++. Понятие числового ряда и его суммы. Критерий Коши сходимости ряда. Необходимое условие сходимости.
- •12+. Признаки Даламбера и Коши сходимости рядов с неотрицательными членами.
- •13. Интегральный признак Коши сходимости числового ряда.
- •14++. Знакопеременные числовые ряды. Абсолютная и условная сходимость. Знакочередующиеся ряды. Признак Лейбница.
- •15++. Функциональный ряд. Сумма ряда. Определение равномерной сходимости ряда. Критерий Коши равномерной сходимости функционального ряда.
- •16+. Признак Вейерштрасса равномерной сходимости.
- •17++. Свойства равномерно сходящихся функциональных рядов. Теорема о непрерывности суммы равномерно сходящегося ряда из непрерывных функций. Теорема о почленном интегрировании и дифференцировании ряда (без доказательства).
- •18+-(нет доказательства теоремы). Степенной ряд. Теорема Абеля.
- •19++. Радиус сходимости степенного ряда. Формула Коши-Адамара для радиуса сходимости степенного ряда.
- •20+. Вопрос для консультации – надо ли доказывать? На лекциях Михайлов не доказывал!
- •Кроме того – лучше его переспросить еще раз и саму теорему, так как в его интерпретации она отличается от общепринятой формулировки, в которой требуется только лишь существование всех производных, а вовсе не их ограниченность ≤ n!!!
- •Ряд Тейлора. Теорема Тейлора о разложимости функции в ряд Тейлора. Разложение основных элементарных функций в ряд Тейлора-Маклорена: ex, sinx, cosx, (1+x)a, ln(1+x).
- •21++. Ряд Фурье. Разложение функций: в общий ряд Фурье, в ряд по синусам, в ряд по косинусам.
- •22-. Функции многих переменных. Понятие n-мерного евклидового пространства. Множество точек евклидового пространства. Последовательность точек и ее предел. Определение функции нескольких переменных.
- •23-. Предел функции нескольких переменных. Непрерывность функции. Частные производные.
- •24+--. Определение дифференцируемой функции нескольких переменных и ее дифференциала. Производные и дифференциалы высших порядков.
- •25++?-по Тейлору, у меня нет этой лекции. Формула Тейлора для функции многих переменных. Экстремум функции нескольких переменных. Необходимое условие экстремума. Достаточное условие экстремума.
- •26+. Двойной интеграл и его свойства. Сведение двойного интеграла к повторному.
- •27+. Тройной интеграл, сведение его к повторному.
- •28. Замена переменных в двойном интеграле. Пример: случай полярных координат.
- •29. Замена переменных в тройном интеграле. Цилиндрические и сферические координаты.
- •30. Вычисление площади гладкой поверхности, заданной параметрически и в явном виде.
- •32+нет доказательства!. Формула Грина. Условия независимости криволинейного интеграла от пути интегрирования.
- •33. Поверхностные интегралы первого и второго рода, их основные свойства и вычисление.
- •35. Формула Стокса, ее запись в координатной и векторной (инвариантной) формах.
- •36. Скалярное и векторное поля. Градиент, дивергенция, ротор. Потенциальное и соленоидальное поля.
- •37. Оператор Гамильтона. (набла) его применение (примеры).
- •38. Основные понятия, относящиеся к обыкновенным дифференциальным уравнениям (ОДУ) первого порядка: общее и частное решения, общий интеграл, интегральная кривая. Задача Коши, ее геометрический смысл.
- •39++. Интегрирование ОДУ первого порядка с разделяющимися переменными и однородных.
- •40++. Интегрирование линейных ОДУ первого порядка и уравнения Бернулли.
- •41++. Интегрирование ОДУ первого порядка в полных дифференциалах. Интегрирующий множитель.
- •42++. Дифференциальные уравнения первого порядка, неразрешенные относительно производной. Метод введения параметра.
- •43. Уравнение n-го порядка с постоянными коэффициентами. Характеристическое уравнение. Фундаментальная система решений (ФСР) однородного уравнения, общее решение неоднородного уравнения.
- •44. Система линейных дифференциальных уравнений первого порядка. ФСР однородной системы. Общее решение однородной системы.

Оглавление |
|
|
1*. Определенный интеграл. Интегральная сумма. Верхняя и нижняя интегральные суммы. Их свойства......................................................................... |
3 |
|
2**. Ограниченность интегрируемой функции............................................................................................................................................................................ |
4 |
|
3**(-). Критерий интегрируемости ограниченной на отрезке функции.................................................................................................................................... |
4 |
|
4≠. Теорема об интегрируемости монотонной на отрезке, а также непрерывной на отрезке функций................................................................................. |
4 |
|
5*. Основные свойства определенного интеграла....................................................................................................................................................................... |
4 |
|
6*. Формула среднего значения для определенного интеграла.................................................................................................................................................. |
7 |
|
7. Интеграл с переменным верхним пределом. Его непрерывность и дифференцируемость................................................................................................. |
7 |
|
8. Формула Ньютона-Лейбница для определенного интеграла.................................................................................................................................................. |
8 |
|
9. Вычисление определенного интеграла по частям и заменой переменной............................................................................................................................ |
8 |
|
10. |
Применение определенного интеграла (площадь плоской фигуры, длина дуги кривой, объем тела вращения)........................................................... |
9 |
11++. Понятие числового ряда и его суммы. Критерий Коши сходимости ряда. Необходимое условие сходимости........................................................ |
11 |
|
12+. Признаки Даламбера и Коши сходимости рядов с неотрицательными членами........................................................................................................... |
12 |
|
13. |
Интегральный признак Коши сходимости числового ряда................................................................................................................................................. |
13 |
14++. Знакопеременные числовые ряды. Абсолютная и условная сходимость. Знакочередующиеся ряды. Признак Лейбница..................................... |
13 |
|
15++. Функциональный ряд. Сумма ряда. Определение равномерной сходимости ряда. Критерий Коши равномерной сходимости функционального |
||
ряда................................................................................................................................................................................................................................................. |
14 |
|
16+. Признак Вейерштрасса равномерной сходимости............................................................................................................................................................ |
15 |
|
17++. Свойства равномерно сходящихся функциональных рядов. Теорема о непрерывности суммы равномерно сходящегося ряда из непрерывных |
||
функций. Теорема о почленном интегрировании и дифференцировании ряда (без доказательства)................................................................................... |
15 |
|
18+-(нет доказательства теоремы). Степенной ряд. Теорема Абеля........................................................................................................................................ |
16 |
|
19++. Радиус сходимости степенного ряда. Формула Коши-Адамара для радиуса сходимости степенного ряда.............................................................. |
17 |
|
20+. Вопрос для консультации – надо ли доказывать? На лекциях Михайлов не доказывал!.............................................................................................. |
17 |
|
Кроме того – лучше его переспросить еще раз и саму теорему, так как в его интерпретации она отличается от общепринятой формулировки, в |
|
|
которой требуется только лишь существование всех производных, а вовсе не их ограниченность ≤ n!!!.......................................................................... |
17 |
|
Ряд Тейлора. Теорема Тейлора о разложимости функции в ряд Тейлора. Разложение основных элементарных функций в ряд Тейлора-Маклорена: ex, |
||
sinx, cosx, (1+x)a, ln(1+x)............................................................................................................................................................................................................... |
17 |
|
21++. Ряд Фурье. Разложение функций: в общий ряд Фурье, в ряд по синусам, в ряд по косинусам................................................................................. |
19 |
|
22-. Функции многих переменных. Понятие n-мерного евклидового пространства. Множество точек евклидового пространства. |
|
|
Последовательность точек и ее предел. Определение функции нескольких переменных.................................................................................................... |
20 |
|
23-. Предел функции нескольких переменных. Непрерывность функции. Частные производные...................................................................................... |
21 |
|
24+--. Определение дифференцируемой функции нескольких переменных и ее дифференциала. Производные и дифференциалы высших порядков. |
||
......................................................................................................................................................................................................................................................... |
|
22 |
25++?-по Тейлору, у меня нет этой лекции. Формула Тейлора для функции многих переменных. Экстремум функции нескольких переменных. |
|
|
Необходимое условие экстремума. Достаточное условие экстремума.................................................................................................................................... |
25 |
|
26+. Двойной интеграл и его свойства. Сведение двойного интеграла к повторному........................................................................................................... |
27 |
|
27+. Тройной интеграл, сведение его к повторному.................................................................................................................................................................. |
28 |
|
28. |
Замена переменных в двойном интеграле. Пример: случай полярных координат........................................................................................................... |
29 |
29. |
Замена переменных в тройном интеграле. Цилиндрические и сферические координаты.............................................................................................. |
29 |
30. |
Вычисление площади гладкой поверхности, заданной параметрически и в явном виде................................................................................................ |
31 |
31. |
Определение криволинейных интегралов первого и второго рода, их основные свойства и вычисление.................................................................... |
31 |
32+нет доказательства!. Формула Грина. Условия независимости криволинейного интеграла от пути интегрирования................................................. |
33 |
|
33. |
Поверхностные интегралы первого и второго рода, их основные свойства и вычисление............................................................................................. |
33 |
34. |
Теорема Гаусса-Остроградского, ее запись в координатной и векторной (инвариантной) формах................................................................................ |
34 |
35. |
Формула Стокса, ее запись в координатной и векторной (инвариантной) формах.......................................................................................................... |
35 |
36. |
Скалярное и векторное поля. Градиент, дивергенция, ротор. Потенциальное и соленоидальное поля......................................................................... |
36 |
37. |
Оператор Гамильтона. (набла) его применение (примеры)............................................................................................................................................ |
37 |
38. |
Основные понятия, относящиеся к обыкновенным дифференциальным уравнениям (ОДУ) первого порядка: общее и частное решения, общий |
|
интеграл, интегральная кривая. Задача Коши, ее геометрический смысл.............................................................................................................................. |
37 |
|
39++. Интегрирование ОДУ первого порядка с разделяющимися переменными и однородных......................................................................................... |
38 |
|
40++. Интегрирование линейных ОДУ первого порядка и уравнения Бернулли................................................................................................................... |
39 |
|
41++. Интегрирование ОДУ первого порядка в полных дифференциалах. Интегрирующий множитель........................................................................... |
39 |
|
42++. Дифференциальные уравнения первого порядка, неразрешенные относительно производной. Метод введения параметра................................. |
41 |
|
43. |
Уравнение n-го порядка с постоянными коэффициентами. Характеристическое уравнение. Фундаментальная система решений (ФСР) |
|
однородного уравнения, общее решение неоднородного уравнения....................................................................................................................................... |
42 |
|
44. |
Система линейных дифференциальных уравнений первого порядка. ФСР однородной системы. Общее решение однородной системы............... |
45 |
* - максимально близко к лекциям Михайлова В.Д. в 2015 (общий ход совпадает, отличия не существенны. Возможно другие обозначения.) ** - абсолютно идентично лекциям Михайлова В.Д. в 2015 **(-) – так у М.В.Д., но почему именно так, не до конца ясно (по крайней мере мне). В тексте есть пометки, что именно не ясно.
≠ - проверено, но М.В.Д. не соответствует.
Все остальное – скорее всего правильно, но на идентичность М.В.Д. не проверялось.
1
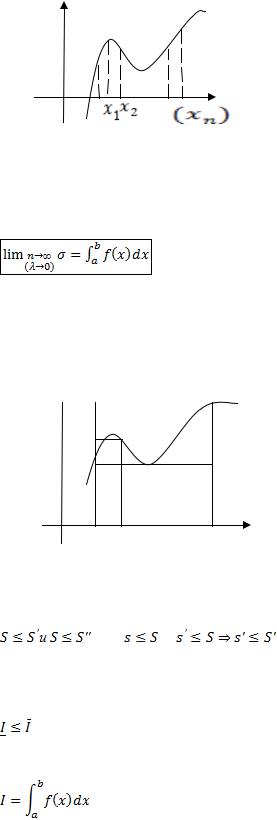
1*. Определенный интеграл. Интегральная сумма. Верхняя и нижняя интегральные суммы. Их свойства.
Пусть на некотором промежутке 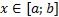 задана функция
задана функция 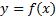 .
.
y
a |
b x |
Произведём разбиение отрезка 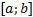 точками
точками 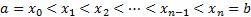 . Внутри каждого отрезка
. Внутри каждого отрезка 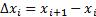 возьмём произвольную точку
возьмём произвольную точку 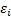 .
.
 - интегральная сумма.
- интегральная сумма.
Устремим 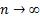 . Максимум
. Максимум 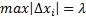 - мелкость разбиения (характеристика разбиения). (по М.В.Д это - ∆, далее, во всех вопросах, будет использоваться и то и другое обозначения, чтобы не исправлять все лямбды в формулах).
- мелкость разбиения (характеристика разбиения). (по М.В.Д это - ∆, далее, во всех вопросах, будет использоваться и то и другое обозначения, чтобы не исправлять все лямбды в формулах).
Фигура под кривой называется криволинейной трапецией.
- определение определенного интеграла (если предел существует).
Интегральные суммы и их свойства:
Нижняя интегральная сумма: 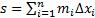 , где
, где 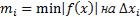 Верхняя интегральная сумма:
Верхняя интегральная сумма: 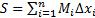 , где
, где 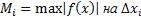
1) 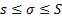 , при данном конкретном разбиении.
, при данном конкретном разбиении.
2) если разбиение T' получается из разбиения T добавлением одной точки разбиения, то нижняя интегральная сумма может только увеличиться, а верхняя только уменьшиться, т.е. 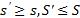
y
 M
M
mi
|
'i |
|
|
m |
|
|
|
|
|
|
|
|
|
i |
|
|
|
|
|
xi x' |
xi |
x |
||
Следствие: при добавленииi к любому разбиению T любого дополнительного числа точек разбиения нижняя интегральная сумма может только увеличиться, а верхняя - только уменьшиться+1.
3) Для любых 2-х разбиений T' и T'', нижняя интегральная сумма любого разбиения не превосходит интегральную сумму другого разбиения 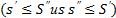 .
.
Доказательство: по предыдущему свойству рассмотрим разбиение T, полученное из всех точек разбиения T' и T''. Тогда 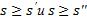 . Аналогично
. Аналогично
. И т.к. |
, то |
, что и требовалось доказать. |
4) Все нижние интегральные суммы ограничены сверху, а все верхние интегральные суммы ограничены снизу. Как известно, множество чисел, ограниченных сверху имеют точную верхнюю грань 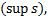 аналогично и для ограниченных снизу - нижняя грань
аналогично и для ограниченных снизу - нижняя грань 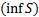 .
.
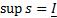 - верхняя грань для s (нижний интеграл Дарбу, именно так! Точная верхняя грань нижних инт.сумм = нижний инт.Дарбу).
- верхняя грань для s (нижний интеграл Дарбу, именно так! Точная верхняя грань нижних инт.сумм = нижний инт.Дарбу). 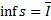 - нижняя грань для S (верхний интеграл Дарбу).
- нижняя грань для S (верхний интеграл Дарбу).
Геометрический смысл определенного интеграла - это площадь фигуры, ограниченной прямыми 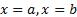 , осью
, осью 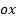 и графиком функции
и графиком функции 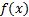 .
.
Основные свойства определённого интеграла.
b
1) f (x)dx - не зависит от названия переменной a
2) 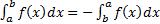
3) 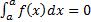 ;
;
4) 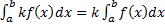 5)
5) 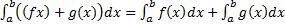 ; (следует из определения интеграла как предела интегральных сумм).
; (следует из определения интеграла как предела интегральных сумм).
6)Если f(x) и g(x) интегрируемы на [a,b], то f(x)∙g(x) интегрируемы на [a,b]
7)Если [a,b] разбить точкой C на два интервала: [a,c] и [c,b], то:
2

-Из интегрируемости f(x) на [a,b] => интегрируемость f(x) на [a,c] и [c,b],
-Из интегрируемости f(x) на [a,c] и [c,b] => интегрируемость f(x) на [a,b],
- 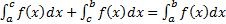
|
|
b |
8) |
Если f(x) интегрируема на [a,b] и для x [a,b] : m, M :m f (x) M , то m (b a) f (x)dx M (b a) |
|
|
|
a |
9) |
Если f(x) интегрируема на [a,b], то |f(x)| интегрируема на [a,b] и |
; |
2**. Ограниченность интегрируемой функции.
Если функция интегрируема на отрезке, то она ограничена на этом отрезке.
Замечание: условие ограниченности является необходимым условием интегрируемости функции по Риману на отрезке. Доказательство:
От противного. Предположим, что функция не ограничена на [a,b], при составлении интегральной суммы
, если ф-я не ограничена => она не ограничена по крайней мере на одном отрезке разбиения, поэтому в выражении для σ по крайней мере одно из слагаемых неограниченно => вся сумма неограниченна => lim σ не равен конечному числу, т.е. интеграл не существует. Противоречие.
3**(-). Критерий интегрируемости ограниченной на отрезке функции.
Необходимое и достаточное условие существования опред.интеграла состоит в том, что для 0 : такое разбиение отрезка, что S-s≤ε.
|
интеграл |
b |
|
Необходимость: |
f(x)dx I lim |
||
|
|
n |
|
|
|
||
|
|
a |
0 |
. Доказать, что для 0 : такое разбиение отрезка, что S-s≤ε.
Т.к. существует lim σ = I => 0 оценим разность S-s = S – σ + σ – I + I – s:
|S – s| ≤ |S – σ| + |I – σ| + |I – s| ≤ (соответственно:) ε/4 (почему?) + ε/4 (по определению предела) + ε/4 (почему?) ≤ ¾ ε < ε
|
|
|
|
|
I |
lim |
Достаточность: дано: 0 : разбиение: S – s<ε. Доказать, что ф-я интегрируема, т.е. |
n . |
|||||
|
|
|
|
|
|
0 |
S – s < ε |
|
|
|
|
||
|
|
- для в.и.Дарбу при 0 : такое разбиение, что S – |
|
|
≤ ε/2 (из определения inf S) |
|
|
I |
I |
|
|||
Аналогично для I : при 0 : такое разбиение, что |
I – s≤ ε/2 (из определения sup s) |
|
||||
Складываем неравенства: S – I + I – s ≤ ε, но нам дано, что S – s<ε => I – I ≤ ε => I = I = I => S – I < ε => lim S = I => I = lim σ.
4≠. Теорема об интегрируемости монотонной на отрезке, а также непрерывной на отрезке функций.
Следствие №3 (из критерия Коши) :
Если f(x) ограничена и монотонна на [a, b], то она интегрируема на этом отрезке. Доказательство:
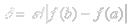 ;
; 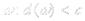
в силу монотонности функции все разности под знаком модуля в получившейся сумме имеют один знак
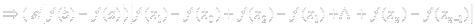 {т.к.
{т.к. 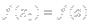 и
и 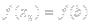 }=
}=  ч.т.д.
ч.т.д.
Следствие №2 (из критерия Коши) :
Если функция f непрерывна на отрезке [a, b], то она интегрируема на этом отрезке. Доказательство:
f - непрерывна на [a, b] 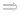 она равномерно
она равномерно
непрерывна
3

ч.т.д.
5*. Основные свойства определенного интеграла.
Основные свойства определённого интеграла. (приведены в порядке и составе М.В.Д., так что в дальнейших доказательствах ссылки в формулах не соответствуют порядку данных свойств)
b
1) f (x)dx - не зависит от названия переменной a
2) 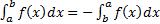
3) 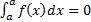 ;
;
4) 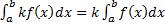 5)
5) 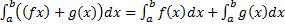 ; (следует из определения интеграла как предела интегральных сумм).
; (следует из определения интеграла как предела интегральных сумм).
6)Если f(x) и g(x) интегрируемы на [a,b], то f(x)∙g(x) интегрируемы на [a,b]
7)Если [a,b] разбить точкой C на два интервала: [a,c] и [c,b], то:
-Из интегрируемости f(x) на [a,b] => интегрируемость f(x) на [a,c] и [c,b],
-Из интегрируемости f(x) на [a,c] и [c,b] => интегрируемость f(x) на [a,b],
- 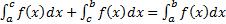
b
8) |
Если f(x) интегрируема на [a,b] и для x [a,b] : m, M :m f (x) M , то m (b a) f (x)dx M (b a) |
||
|
|
|
a |
|
b |
|
|
- Следствие 1: Если для любого х из [a,b] f(x)≥0 и f(x) – интегрируема на [a,b] => f (x)dx ≥ 0 |
|
|
|
|
a |
|
|
|
b |
|
b |
- Следствие 2: Если f(x) и g(x) интегрируемы на [a,b] и для любого х из [a,b] f(x) ≥ g(x) => f (x)dx |
≥ g(x)dx |
||
|
a |
|
a |
9) |
Если f(x) интегрируема на [a,b], то |f(x)| интегрируема на [a,b] и |
; |
|
(Михайлов не называл свойства линейностью и аддитивностью и доказывал несколько иначе и не всегда то , но и так сойдет)
Линейность. Если функции f(x), g(x) интегрируемы по отрезку [a,b] , то по этому отрезку интегрируема их линейная комбинация A f(x) + B g(x) (A, B = const), и
(лучше без A и B, чтобы соответствовало одному их свойств выше, но можно и так, просто тогда это будет доказательством сразу двух свойств по М.В.Д. – 4 и 5).
Док-во: для любого разбиения отрезка и любого выбора точек |
выполняется |
Перейдем в этом равенстве к пределу при |
. Так как существуют пределы интегральных сумм, стоящих в левой части равенства, то существует |
предел линейной комбинации этих сумм, следовательно, существует предел правой интегральной суммы, откуда следует истинность и утверждения, и равенства.
Аддитивность. Если y = f(x) интегрируема по отрезку [a,b] и точка c принадлежит этому отрезку, то 
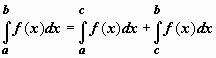 .
.
Док-во. Если f(x) удовлетворяет условиям интегрируемости по отрезку [a,b], то она удовлетворяет условиям интегрируемости по отрезкам [a,c] и [c,b]. Будем брать такие разбиения отрезка [a,b] , чтобы точка c являлась одним из узлов xi: c = xi. Тогда
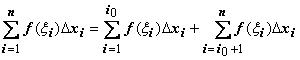 .
.
4

В этом равенстве первая сумма справа - интегральная сумма для |
, вторая - для |
. Переходим к пределу при |
. Пределы для |
всех трёх сумм существуют, и |
. |
|
|
Свойство аддитивности остаётся верным при любом расположении точек, если только функция интегрируема по самому широкому интервалу. Пусть, например, c < b < a, и f(x) интегрируема по [c, a]. Тогда, по доказанному, . Отсюда и из определения интеграла для случая, когда нижний предел больше верхнего, следует, что
.
Интеграл от единичной функции ( f(x) = 1). Если f(x) = 1, то
.
Док-во. Если f(x) = 1 , то для любого разбиения
= xn - x0 = b – a, т.е любая интегральная сумма равна длине отрезка. Предел постоянной равен этой постоянной, откуда и следует доказываемое утверждение.
Теорема об интегрировании неравенств. (В случае М.В.Д. – это не теорема, а следствие свойства 8)
Если в любой точке |
выполняется неравенство |
, и функции f(x), g(x) интегрируемы по отрезку [a,b], то |
|
. |
|
Док-во. Для любого разбиения отрезка и любого выбора точек |
при |
|
. Переходя в этом неравенстве к пределу при
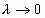 , получаем требуемое неравенство.
, получаем требуемое неравенство.
Теоремы об оценке интеграла. (а вот и само св-во 8 по М.В.Д. – на всякий случай лучше и не называть его теоремой, а доказать как свойство.) 1. Если на отрезке [a,b] функция удовлетворяет неравенству 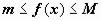 , то
, то 

.
Док-во. Докажем левое неравенство (цифрами над знаками импликации обозначены номера применяемых ранее доказанных свойств):
Аналогично доказывается и правое неравенство. |
. |
|
|
|
|
2. Если функция f(x) интегрируема по отрезку [a,b], то |
. |
|
Док-во. |
|
|
|
|
. |
Теорема о среднем. Если f(x) непрерывна на отрезке [a,b], то существует точка |
, такая что |
. |
Док-во. Функция, непрерывная на отрезке, принимает на этом отрезке своё наименьшее m и наибольшее M значения. Тогда |
|
|
5
