
- •1*. Определенный интеграл. Интегральная сумма. Верхняя и нижняя интегральные суммы. Их свойства.
- •2**. Ограниченность интегрируемой функции.
- •3**(-). Критерий интегрируемости ограниченной на отрезке функции.
- •4≠. Теорема об интегрируемости монотонной на отрезке, а также непрерывной на отрезке функций.
- •5*. Основные свойства определенного интеграла.
- •6*. Формула среднего значения для определенного интеграла.
- •7. Интеграл с переменным верхним пределом. Его непрерывность и дифференцируемость.
- •8. Формула Ньютона-Лейбница для определенного интеграла.
- •9. Вычисление определенного интеграла по частям и заменой переменной.
- •10. Применение определенного интеграла (площадь плоской фигуры, длина дуги кривой, объем тела вращения).
- •11++. Понятие числового ряда и его суммы. Критерий Коши сходимости ряда. Необходимое условие сходимости.
- •12+. Признаки Даламбера и Коши сходимости рядов с неотрицательными членами.
- •13. Интегральный признак Коши сходимости числового ряда.
- •14++. Знакопеременные числовые ряды. Абсолютная и условная сходимость. Знакочередующиеся ряды. Признак Лейбница.
- •15++. Функциональный ряд. Сумма ряда. Определение равномерной сходимости ряда. Критерий Коши равномерной сходимости функционального ряда.
- •16+. Признак Вейерштрасса равномерной сходимости.
- •17++. Свойства равномерно сходящихся функциональных рядов. Теорема о непрерывности суммы равномерно сходящегося ряда из непрерывных функций. Теорема о почленном интегрировании и дифференцировании ряда (без доказательства).
- •18+-(нет доказательства теоремы). Степенной ряд. Теорема Абеля.
- •19++. Радиус сходимости степенного ряда. Формула Коши-Адамара для радиуса сходимости степенного ряда.
- •20+. Вопрос для консультации – надо ли доказывать? На лекциях Михайлов не доказывал!
- •Кроме того – лучше его переспросить еще раз и саму теорему, так как в его интерпретации она отличается от общепринятой формулировки, в которой требуется только лишь существование всех производных, а вовсе не их ограниченность ≤ n!!!
- •Ряд Тейлора. Теорема Тейлора о разложимости функции в ряд Тейлора. Разложение основных элементарных функций в ряд Тейлора-Маклорена: ex, sinx, cosx, (1+x)a, ln(1+x).
- •21++. Ряд Фурье. Разложение функций: в общий ряд Фурье, в ряд по синусам, в ряд по косинусам.
- •22-. Функции многих переменных. Понятие n-мерного евклидового пространства. Множество точек евклидового пространства. Последовательность точек и ее предел. Определение функции нескольких переменных.
- •23-. Предел функции нескольких переменных. Непрерывность функции. Частные производные.
- •24+--. Определение дифференцируемой функции нескольких переменных и ее дифференциала. Производные и дифференциалы высших порядков.
- •25++?-по Тейлору, у меня нет этой лекции. Формула Тейлора для функции многих переменных. Экстремум функции нескольких переменных. Необходимое условие экстремума. Достаточное условие экстремума.
- •26+. Двойной интеграл и его свойства. Сведение двойного интеграла к повторному.
- •27+. Тройной интеграл, сведение его к повторному.
- •28. Замена переменных в двойном интеграле. Пример: случай полярных координат.
- •29. Замена переменных в тройном интеграле. Цилиндрические и сферические координаты.
- •30. Вычисление площади гладкой поверхности, заданной параметрически и в явном виде.
- •32+нет доказательства!. Формула Грина. Условия независимости криволинейного интеграла от пути интегрирования.
- •33. Поверхностные интегралы первого и второго рода, их основные свойства и вычисление.
- •35. Формула Стокса, ее запись в координатной и векторной (инвариантной) формах.
- •36. Скалярное и векторное поля. Градиент, дивергенция, ротор. Потенциальное и соленоидальное поля.
- •37. Оператор Гамильтона. (набла) его применение (примеры).
- •38. Основные понятия, относящиеся к обыкновенным дифференциальным уравнениям (ОДУ) первого порядка: общее и частное решения, общий интеграл, интегральная кривая. Задача Коши, ее геометрический смысл.
- •39++. Интегрирование ОДУ первого порядка с разделяющимися переменными и однородных.
- •40++. Интегрирование линейных ОДУ первого порядка и уравнения Бернулли.
- •41++. Интегрирование ОДУ первого порядка в полных дифференциалах. Интегрирующий множитель.
- •42++. Дифференциальные уравнения первого порядка, неразрешенные относительно производной. Метод введения параметра.
- •43. Уравнение n-го порядка с постоянными коэффициентами. Характеристическое уравнение. Фундаментальная система решений (ФСР) однородного уравнения, общее решение неоднородного уравнения.
- •44. Система линейных дифференциальных уравнений первого порядка. ФСР однородной системы. Общее решение однородной системы.
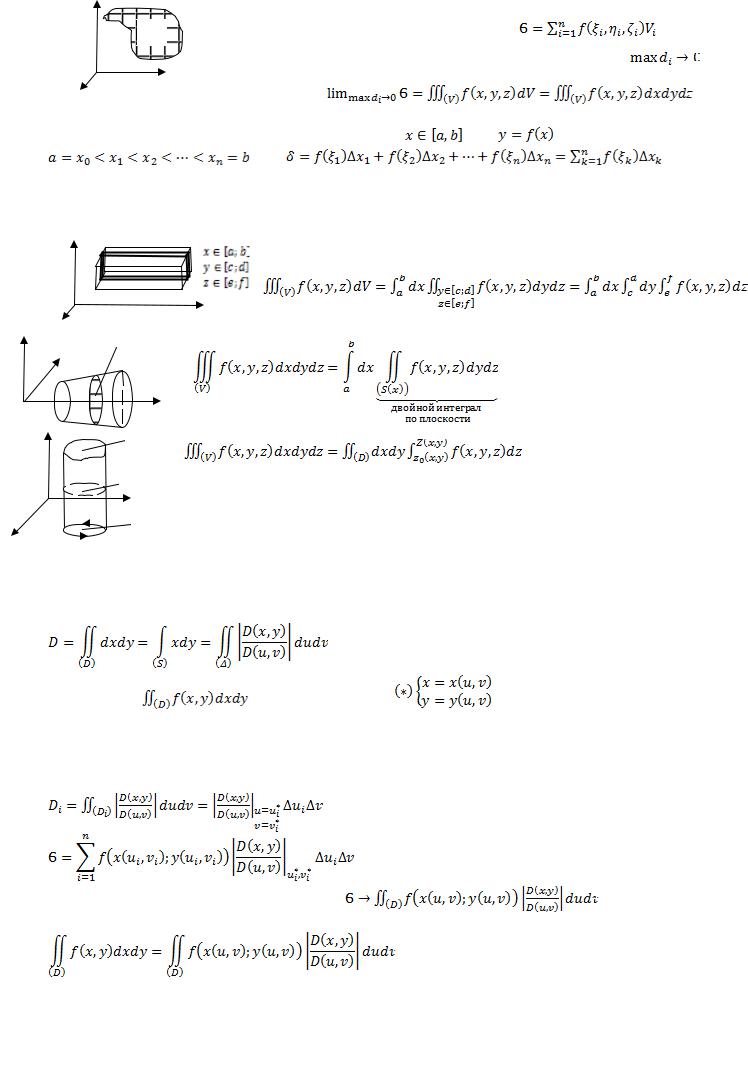
27+. Тройной интеграл, сведение его к повторному.
z |
|
|
Определение тройного интеграла. Пусть в некоторой трехмерной области (V) с границей (S) задана в каждой точке |
|
|
|
функция f(x,y,z). Разобьём тело (V) сеткой поверхностей на частичные области (Vi). В каждой (Vi) возьмём |
||
|
(V) |
(S) |
произвольную точку (ξi, ηi, ζi) и составим интегральную сумму: |
. Устремим |
|
|
|||
x |
|
y |
максимальный диаметр (макс. расстояние между любой парой точек в области) к нулю: |
, а |
|
количество разбиений к бесконечности: n→∞. Тогда, если существует предел интегральных сумм, то он равен |
|||
|
|
|||
|
|
|
||
|
|
|
тройному интегралу: |
. |
(в пределе выше надо еще указать, что n→∞) |
|
|
На всякий случай определение интегральной суммы. Пусть на нек-ом отрезке |
задана |
. Произведём разбиение отрезка: |
. Число |
|
, называется |
интегральной суммой функции f(x), соответствующей данному разбиению T(ξi;xi) сегмента [a;b] и данному выбору промежуточных точек ξi на частичных сегментах [xi-1;xi], –хар-тика разбиения: 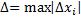
z |
|
|
f |
|
a |
|
|
|
|
e |
|
|
|
|
|
|
b |
|
|
x |
c |
d |
y |
|
Сведение к повторному интегралу. Рассмотрим первый простейший случай. Пусть тело V – прямоугольный параллелепипед. Проведём секущую плоскость. Возьмём приращение плоскости (жирные линии). Тогда:
.
|
|
|
S(x) |
Рассмотрим второй случай. |
z |
|
|
|
|
y |
|
|
|
|
|
|
|
|
|
|
|
(V) |
|
x |
|
a |
|
b |
|
|
|
|
||
|
z |
|
Z(x,y) |
Рассмотрим третий случай – область (V) цилиндрического типа. |
|
|
|
||
|
|
|
|
|
|
|
|
z0(x,y) |
|
|
|
|
y |
|
x |
|
|
D(x,y) |
|
|
|
(C) |
|
|
|
|
|
|
28. Замена переменных в двойном интеграле. Пример: случай полярных координат.
Вычислим интеграл |
, используя замену переменных |
. Рассмотрим интеграл как предел интегральных сумм. |
Область (D) сеткой кривых разделяется на частичные области Di, внутри каждой частичной области берём произвольные точки (xi, yi). Составляем интегральную сумму: 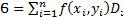 , где Di – площадь i-ой частичной области. Устремим максимальный диаметр к нулю:
, где Di – площадь i-ой частичной области. Устремим максимальный диаметр к нулю:  . По
. По
определению, 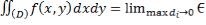 . Совершим замену переменных (*). При замене (*) площадь
. Совершим замену переменных (*). При замене (*) площадь
.
Если 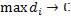 , то
, то 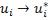 и
и 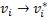 , следовательно,
, следовательно,
28

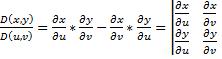 – якобиан преобразования (*).
– якобиан преобразования (*).
y
|
D |
y |
|
ρ |
x |
φ |
|
|
x |
Пример с полярными координатами. 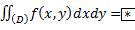
z
(S)
(V)
y
29. Замена переменных в тройном интеграле. Цилиндрические и сферические координаты.
|
|
Замена переменных в тройном интеграле в общем случае. |
||
x |
|
Пусть имеется тело (V) с границей (S). |
|
|
(D) |
(L) |
|
||
|
|
|
||
|
|
Пусть |
, тогда |
. |
Замена:
Преобразование (*) будем считать взаимно-однозначным, то есть всё можно выразить друг через друга, а именно:
ζ
(Λ)
(Δ)
η
ξ
Пусть поверхность (Λ) задаётся параметрически, то есть: Получаем параметрическое задание поверхности (S) (см. рис. ниже).
v
(Σ)
u
29
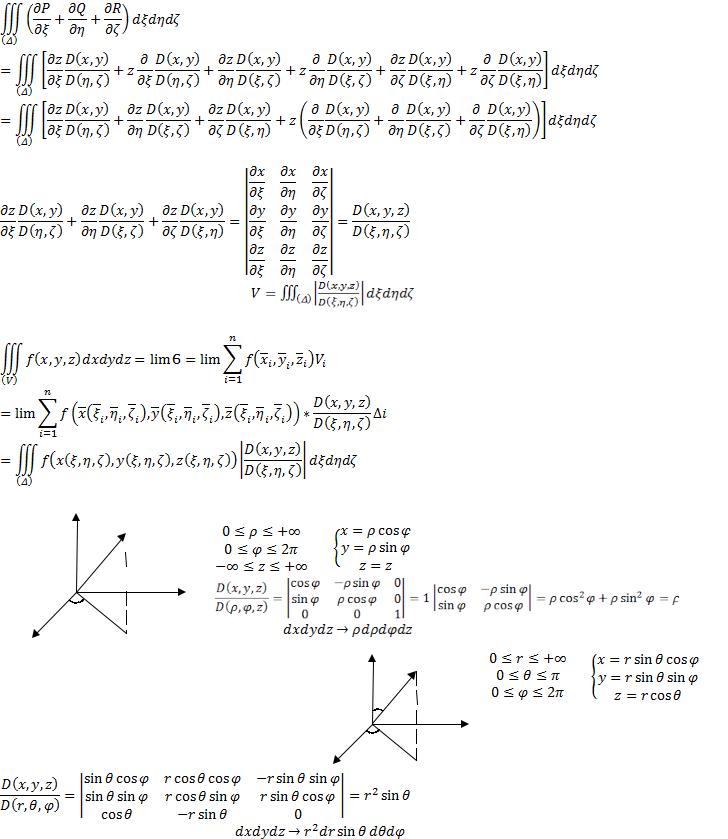
Два последних двойных интеграла равны, так как: 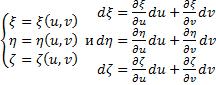 Применим к последнему выражению формулу Гаусса-Остроградского, то есть эту формулу:
Применим к последнему выражению формулу Гаусса-Остроградского, то есть эту формулу:
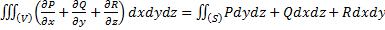 . Пусть
. Пусть 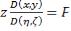 ,
,  ,
, 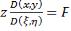 , тогда:
, тогда:
Выражение в скобках равно нулю. Оставшееся выражение запишем так:
Это якобиан преобразования. Окончательно получаем:
А для общего случая:
z |
|
|
Цилиндрические координаты: |
|
M(x,y,z) |
Переходим от координаты M(x,y,z) к M(ρ,φ,z). Это цилиндрические координаты, где: |
|
|
|
|
|
0 |
|
z |
y |
|
|||
|
|||
|
|
φρ
x |
Получаем, что |
|
|
. |
|
|
|
|
|
||
|
Сферические |
z |
|
|
координаты: |
|
|
|
M(x,y,z) |
|
|
|
|
|
|
|
|
|
|
|
θ |
r |
|
|
|
|
z |
|
|
|
|
0 |
|
y |
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
φ |
|
|
|
|
x |
|
|
|
Получаем элемент объёма сферических координат: |
. |
30. Вычисление площади гладкой поверхности, заданной параметрически и в явном виде.
30

z (L) |
γ |
Рассмотрим кусок поверхности |
S, заданной уравнением F=(x,y,z)=0. |
Пусть выполняется |
условие |
|||
|
|
|
|
|
|
|
||
(S) |
M |
|
|
, что означает, что в каждой точке поверхности существует нормаль с |
||||
|
|
|
||||||
|
y |
направляющим |
вектором |
. Разобьем поверхность S сеткой гладких кривых на |
||||
|
G |
элементарные |
области |
(разбиение |
Z). Пусть |
– наибольший из |
диаметров |
|
x |
|
|
|
|
|
|
|
|
|
|
элементарных областей. Если независимо от разбиения Z существует |
|
, то |
||||
он и называется площадью данной поверхности. Пусть S однозначно проектируется на плоскость xy и |
G – это проекция. Элементу площади dxdy |
|||||||
области G на плоскости xy соответствует элемент площади поверхности S, равный |
, где |
– угол между нормалью к поверхности S и |
||||||
осью Z. Поэтому вычисление площади поверхности сводится к вычислению двойного интеграла 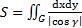 по проекции поверхности на
по проекции поверхности на
плоскость. Если поверхность задана уравнением 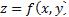 ,
, 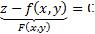 , а нормаль представляет собой градиент функции, то есть:
, а нормаль представляет собой градиент функции, то есть:
, то |
и площадь поверхности вычисляется по формуле: |
, здесь G – проекция поверхности S на плоскость xy.
Если поверхность однозначно проектируется на другие координатные плоскости, то соответственно изменится формула вычисления площади поверхности.
Если кривая задана параметрическими уравнениями 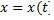 и
и 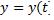 , то площадь криволинейной трапеции, ограниченной этой кривой,
, то площадь криволинейной трапеции, ограниченной этой кривой,
прямыми  и
и 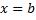 и отрезком [a,b] оси Ox, выражается формулой
и отрезком [a,b] оси Ox, выражается формулой 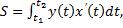 где
где 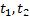 определяются из уравнений
определяются из уравнений
Площадь криволинейного сектора, ограниченного кривой, заданной в полярных координатах уравнением 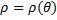 и двумя полярными радиусами
и двумя полярными радиусами
|
|
|
находится по формуле |
. |
y |
|
|
B |
|
|
|
|
|
|
M |
Δlk |
(L) |
31. Определение криволинейных интегралов первого и второго рода, их |
|
основные свойства и вычисление. |
|
|||
|
2 |
|
|
|
M1 |
|
|
|
|
A 
xОпределение криволинейного интеграла первого рода, его основные свойства и вычисление.
Кривая должна быть простой кривой, то есть |
. |
Пусть кривая будет разбита точками разбиения. Составим интегральную сумму. |
|
Полученный интеграл называется криволинейным интегралом первого рода.
31
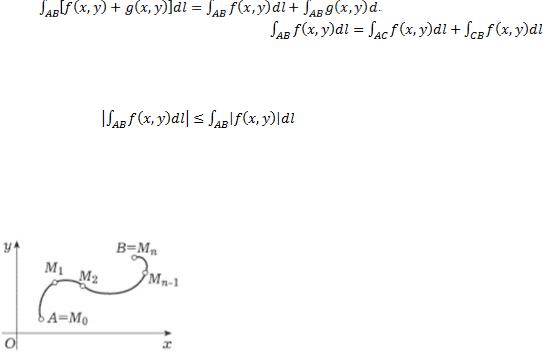
На словах можно сказать так. Если существует предел интегральной суммы (см. выше) при стремлении к нулю наибольшей из длин Δlk (то есть 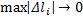 ), то этот предел называется криволинейным интегралом первого рода от функции f(x,y) по кривой L и обозначается символом
), то этот предел называется криволинейным интегралом первого рода от функции f(x,y) по кривой L и обозначается символом 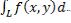 или
или 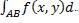 .
.
Если кривая задана не параметрически, а, к примеру, так: 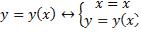 , тогда
, тогда 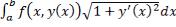 . Основные свойства:
. Основные свойства:
Линейность:
Аддитивность (если дуга AB составлена из двух дуг AC и CB): Монотонность: если f<=g на L, то: 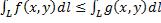 Изменение направления обхода кривой интегрирования не влияет на знак:
Изменение направления обхода кривой интегрирования не влияет на знак: 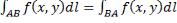
Оценка модуля интеграла:
Вычисление. Пусть L – кривая, как на рисунке, заданная параметрически. Пусть функция f(x,y) определена и интегрируема вдоль кривой l как
криволинейный интеграл первого рода. Тогда: 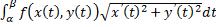 .
.
Таким образом, для вычисления по длине дуги АВ надо, используя параметрическое уравнение кривой, выразить подынтегральную функцию через параметр t, заменить dl дифференциалом дуги в зависимости от параметра t и проинтегрировать полученное выражение по t.
Определение криволинейного интеграла второго рода, его основные свойства и вычисление. Связь с интегралом первого рода.
Пусть кривая L на координатной плоскости Оху задана параметрически уравнениями 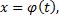
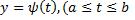 . L называется простой (плоской) незамкнутой кривой, если функции
. L называется простой (плоской) незамкнутой кривой, если функции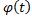 ,
, 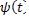 непрерывны на
непрерывны на 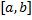 и различным значениям параметра t из сегмента
и различным значениям параметра t из сегмента 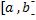 соответствуют
соответствуют
различные точки 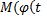 ,
,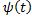 . Если точка
. Если точка 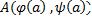 совпадает с точкой
совпадает с точкой 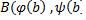 ,
,
а остальные точки не являются кратными, то L называется простой замкнутой кривой. Простая кривая L называется спрямляемой, если существует предел (длинa кривой L) длин ломаных, вписанных в кривую,
при Δt → 0.
Пусть на кривой AB заданы две функции, P(x, y) и Q(x, y). Разобьем сегмент 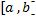 на n частей точками
на n частей точками 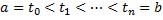 . Кривая АВ разобьется на n частей точками
. Кривая АВ разобьется на n частей точками 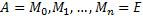 в направлении от A к B. Пусть
в направлении от A к B. Пусть 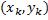 – координаты точки
– координаты точки 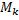 ,
, 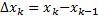 ,
,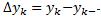 ,
, 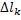 – длина дуги
– длина дуги 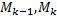 . На каждой дуге
. На каждой дуге 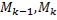 возьмем некоторую точку (координаты
возьмем некоторую точку (координаты 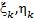 ) и составим две интегральные суммы:
) и составим две интегральные суммы: 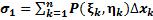 ,
, 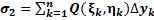 . Если существует предел интегральной суммы
. Если существует предел интегральной суммы 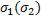 при стремлении к нулю наибольшей из длин
при стремлении к нулю наибольшей из длин 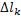 , то этот предел называется криволинейным интегралом второго рода
, то этот предел называется криволинейным интегралом второго рода
 . Сумма
. Сумма 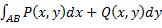 называется общим криволинейным интегралом второго рода. Из определения криволинейного интеграла второго рода следует, что при изменении направления обхода кривой AB изменяется и знак интеграла
называется общим криволинейным интегралом второго рода. Из определения криволинейного интеграла второго рода следует, что при изменении направления обхода кривой AB изменяется и знак интеграла
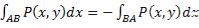 . Аналогично вводится
. Аналогично вводится 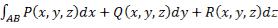 для пространственной
для пространственной
кривой, заданной параметрически 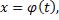
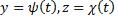 Криволинейные интегралы обладают теми же свойствами, что и обычные определенные: Линейность
Криволинейные интегралы обладают теми же свойствами, что и обычные определенные: Линейность
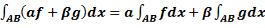 . Аддитивность:
. Аддитивность: 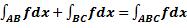 . Монотонность: если f≤g, то
. Монотонность: если f≤g, то
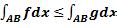 .
.
Кривая L кусочно-гладкая, если она непрерывна и распадается на конечное число не имеющих общих внутренних точек кусков, каждый из которых представляет собой гладкую кривую.
Вычисление криволинейного интеграла второго рода с помощью определенного интеграла.
Если AB – кусочно-гладкая кривая, а функции Р=Р(x,y) и Q=Q(x,y) кусочно непрерывны вдоль кривой AB, то справедливо равенство:
 =
=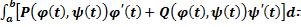 .
.
Если кривая AB задана уравнением y = у(x), a≤x≤b, и имеет кусочно-непрерывную производную, а функции P(x,y) и Q(x,y) кусочно непрерывны вдоль кривой AB, то имеет место равенство: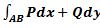 =
=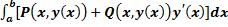 .
.
Связь между криволинейными интегралами первого и второго рода.
Пусть AB− кусочно гладкая кривая, функции Р=P(x,y) и Q=Q(x,y) кусочно непрерывны вдоль кривой AB и 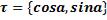 − единичный касательный вектор к кривой AB в точке M(x,y), причем направление
− единичный касательный вектор к кривой AB в точке M(x,y), причем направление соответствует направлению движения от А к В (α − угол между вектором
соответствует направлению движения от А к В (α − угол между вектором  в
в
32
