
- •1*. Определенный интеграл. Интегральная сумма. Верхняя и нижняя интегральные суммы. Их свойства.
- •2**. Ограниченность интегрируемой функции.
- •3**(-). Критерий интегрируемости ограниченной на отрезке функции.
- •4≠. Теорема об интегрируемости монотонной на отрезке, а также непрерывной на отрезке функций.
- •5*. Основные свойства определенного интеграла.
- •6*. Формула среднего значения для определенного интеграла.
- •7. Интеграл с переменным верхним пределом. Его непрерывность и дифференцируемость.
- •8. Формула Ньютона-Лейбница для определенного интеграла.
- •9. Вычисление определенного интеграла по частям и заменой переменной.
- •10. Применение определенного интеграла (площадь плоской фигуры, длина дуги кривой, объем тела вращения).
- •11++. Понятие числового ряда и его суммы. Критерий Коши сходимости ряда. Необходимое условие сходимости.
- •12+. Признаки Даламбера и Коши сходимости рядов с неотрицательными членами.
- •13. Интегральный признак Коши сходимости числового ряда.
- •14++. Знакопеременные числовые ряды. Абсолютная и условная сходимость. Знакочередующиеся ряды. Признак Лейбница.
- •15++. Функциональный ряд. Сумма ряда. Определение равномерной сходимости ряда. Критерий Коши равномерной сходимости функционального ряда.
- •16+. Признак Вейерштрасса равномерной сходимости.
- •17++. Свойства равномерно сходящихся функциональных рядов. Теорема о непрерывности суммы равномерно сходящегося ряда из непрерывных функций. Теорема о почленном интегрировании и дифференцировании ряда (без доказательства).
- •18+-(нет доказательства теоремы). Степенной ряд. Теорема Абеля.
- •19++. Радиус сходимости степенного ряда. Формула Коши-Адамара для радиуса сходимости степенного ряда.
- •20+. Вопрос для консультации – надо ли доказывать? На лекциях Михайлов не доказывал!
- •Кроме того – лучше его переспросить еще раз и саму теорему, так как в его интерпретации она отличается от общепринятой формулировки, в которой требуется только лишь существование всех производных, а вовсе не их ограниченность ≤ n!!!
- •Ряд Тейлора. Теорема Тейлора о разложимости функции в ряд Тейлора. Разложение основных элементарных функций в ряд Тейлора-Маклорена: ex, sinx, cosx, (1+x)a, ln(1+x).
- •21++. Ряд Фурье. Разложение функций: в общий ряд Фурье, в ряд по синусам, в ряд по косинусам.
- •22-. Функции многих переменных. Понятие n-мерного евклидового пространства. Множество точек евклидового пространства. Последовательность точек и ее предел. Определение функции нескольких переменных.
- •23-. Предел функции нескольких переменных. Непрерывность функции. Частные производные.
- •24+--. Определение дифференцируемой функции нескольких переменных и ее дифференциала. Производные и дифференциалы высших порядков.
- •25++?-по Тейлору, у меня нет этой лекции. Формула Тейлора для функции многих переменных. Экстремум функции нескольких переменных. Необходимое условие экстремума. Достаточное условие экстремума.
- •26+. Двойной интеграл и его свойства. Сведение двойного интеграла к повторному.
- •27+. Тройной интеграл, сведение его к повторному.
- •28. Замена переменных в двойном интеграле. Пример: случай полярных координат.
- •29. Замена переменных в тройном интеграле. Цилиндрические и сферические координаты.
- •30. Вычисление площади гладкой поверхности, заданной параметрически и в явном виде.
- •32+нет доказательства!. Формула Грина. Условия независимости криволинейного интеграла от пути интегрирования.
- •33. Поверхностные интегралы первого и второго рода, их основные свойства и вычисление.
- •35. Формула Стокса, ее запись в координатной и векторной (инвариантной) формах.
- •36. Скалярное и векторное поля. Градиент, дивергенция, ротор. Потенциальное и соленоидальное поля.
- •37. Оператор Гамильтона. (набла) его применение (примеры).
- •38. Основные понятия, относящиеся к обыкновенным дифференциальным уравнениям (ОДУ) первого порядка: общее и частное решения, общий интеграл, интегральная кривая. Задача Коши, ее геометрический смысл.
- •39++. Интегрирование ОДУ первого порядка с разделяющимися переменными и однородных.
- •40++. Интегрирование линейных ОДУ первого порядка и уравнения Бернулли.
- •41++. Интегрирование ОДУ первого порядка в полных дифференциалах. Интегрирующий множитель.
- •42++. Дифференциальные уравнения первого порядка, неразрешенные относительно производной. Метод введения параметра.
- •43. Уравнение n-го порядка с постоянными коэффициентами. Характеристическое уравнение. Фундаментальная система решений (ФСР) однородного уравнения, общее решение неоднородного уравнения.
- •44. Система линейных дифференциальных уравнений первого порядка. ФСР однородной системы. Общее решение однородной системы.

точке M(x, y) и осью Oх).  . Для пространственной кривой справедлива аналогичная теорема:
. Для пространственной кривой справедлива аналогичная теорема: .
.
Из лекций:  Это и есть криволинейный интеграл второго рода.
Это и есть криволинейный интеграл второго рода.
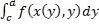 – то же самое, только по y.
– то же самое, только по y.
Каждый интеграл второго рода может быть сведён к первому роду.
или 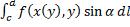
32+нет доказательства!. Формула Грина. Условия независимости криволинейного интеграла от пути интегрирования.
 y
y
Формула Грина: Если C – замкнутая граница области D и функции P(x,y) и Q(x,y) вместе со своими частными производными
(L G |
|
) |
непрерывны в замкнутой области D (включая границу C), то справедлива формула Грина: |
первого порядка |
|
x |
|
|
, причем обход вокруг контура C выбирается так, что область D остается слева. |
Из лекций (не МВД2015): Пусть заданы функции P(x,y) и Q(x,y), которые непрерывны в области D вместе с частными производными первого порядка. Интеграл по границе (L), целиком лежащий в области D и содержащий все точки в области D:  .
.
Положительное направление контура такое, когда ограниченная часть контура находится слева.
Условие независимости криволинейного интеграла 2-го рода от пути интегрирования. Необходимым и достаточным условием того, что криволинейный интеграл первого рода, соединяющий точки M1 и M2, не зависит от пути интегрирования, а зависит только от начальной и конечной точек, является
равенство: 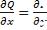 .
.
P(M) M2 
(L)
.
(L')
M1
.
.
33. Поверхностные интегралы первого и второго рода, их основные свойства и вычисление.
 z
z  γ
γ
(S)
– задание поверхности.
 y
y
D
x 
Спроектируем S на плоскость xy, получим область D. Разобьём область D сеткой линий на части, называемые Di. Из каждой точки каждой линии проведём параллельные z линии, тогда и S разделится на Si. Составим интегральную сумму:  . Устремим максимум диаметра Di к
. Устремим максимум диаметра Di к
нулю:  , получим:
, получим:
Это поверхностный интеграл первого рода
33

Так считается поверхностный интеграл первого рода.
Определение вкратце. Если существует конечный предел интегральной суммы, не зависящий от способа разбиения S на элементарные участки Si и от выбора точек, то он называется поверхностным интегралом первого рода.
При переходе от переменных x и y к u и v:
Поверхностный интеграл обладает всеми свойствами обычного интеграла. См. в вопросах выше.
Определение поверхностного интеграла второго рода, его основные свойства и вычисление. Связь с интегралом первого рода.
Пусть задана поверхность S, ограниченная линией L (рис. 3.10). Возьмём на поверхности S какой-нибудь контур L, не
имеющий общих точек с границей L. В точке М контура L можно восстановить две нормали  и
и  к поверхности S.
к поверхности S.
Выберем какое-либо одно из этих направлений. Обводим точку M по контуру L с выбранным направлением нормали.
Если в исходное положение точка M вернётся с тем же направлением нормали (а не с противоположным), то поверхность S называют двусторонней. Мы будем рассматривать только двусторонние поверхности. Двусторонней поверхностью
является всякая гладкая поверхность с уравнением 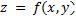 .
.
Пусть S – двусторонняя незамкнутая поверхность, ограниченная линией L, не имеющей точек самопересечения. Выберем определённую сторону поверхности. Будем называть положительным направлением обхода контура L такое направление, при движении по которому по выбранной стороне поверхности сама поверхность остаётся слева. Двусторонняя поверхность с установленным на ней таким образом положительным направлением обхода контуров называется ориентированной поверхностью.
Перейдём к построению поверхностного интеграла второго рода. Возьмём в пространстве двустороннюю поверхность S, состоящую из конечного числа кусков, каждый из которых задан уравнением вида  или является цилиндрической поверхностью с образующими, параллельными оси Oz.
или является цилиндрической поверхностью с образующими, параллельными оси Oz.
Пусть R(x,y,z) – функция, опредёленная и непрерывная на поверхности S. Сетью линий разбиваем S произвольным образом на n "элементарных" участков ΔS1, ΔS2, ..., ΔSi, ..., ΔSn, не имеющих общих внутренних точек. На каждом участке ΔSi произвольным образом выберем точку Mi(xi,yi,zi) (i=1,...,n). Пусть (ΔSi)xy – площадь проекции участка ΔSi на координатную плоскость Оху, взятая со знаком "+", если нормаль к поверхности S в точке Mi(xi,yi,zi) (i=1,...,n) образует с осью Oz острый угол, и со знаком "–", если этот угол тупой. Составим интегральную сумму для функции R(x,y,z) по поверхности S по
переменным x,y:  . Пусть λ – наибольший из диаметров ΔSi (i = 1, ..., n).
. Пусть λ – наибольший из диаметров ΔSi (i = 1, ..., n).
Если существует конечный предел 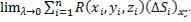 , не зависящий от способа разбиения поверхности S на "элементарные" участки ΔSi и от выбора точек
, не зависящий от способа разбиения поверхности S на "элементарные" участки ΔSi и от выбора точек  , то он называется поверхностным интегралом по выбранной стороне поверхности S от функции
, то он называется поверхностным интегралом по выбранной стороне поверхности S от функции
R(x,y,z) по координатам х, у (или поверхностным интегралом второго рода) и обозначается 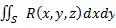 .
.
Аналогично можно построить поверхностные интегралы по координатам x, z или у, z по соответствующей стороне поверхности, т. е.
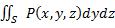 и
и 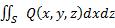 .
.
Если существуют все эти интегралы, то можно ввести "общий" интеграл по выбранной стороне поверхности:
 .
.
Поверхностный интеграл второго рода обладает обычными свойствами интеграла. Заметим лишь, что любой поверхностный интеграл второго рода изменяет знак при перемене стороны поверхности.
Связь между поверхностными интегралами первого и второго рода.
34

Пусть поверхность S задана уравнением: z = f(x,y), причем f(x,y), f'x(x,y), f'y(x,y) — непрерывные функции в замкнутой области τ (проекции поверхности S на координатную плоскость Оху), а функция R(x,y,z) непрерывна на поверхности S. Нормаль к поверхности S, имеющая направляющие косинусы cos α,
cos β, cos γ, выбрана к верхней стороне поверхности S. Тогда  . Для общего случая имеем:
. Для общего случая имеем:
|
= |
|
|
|
|
|
z |
S |
|
|
|||
|
|
(V) |
|
|
34. Теорема Гаусса-Остроградского, ее запись в координатной и |
|
|
|
S1 |
|
|
||
|
|
|
|
|||
|
|
|
|
векторной (инвариантной) формах. |
||
|
|
|||||
|
|
|
|
y |
В координатной форме. Рассмотрим тело (V) в пространстве с ограничивающей поверхностью |
|
|
|
|
|
|||
|
|
|
|
|||
|
|
|
|
|||
|
|
|
|
(S). |
|
|
|
|
|
||||
|
|
|
|
|
|
|
x |
|
|
|
D |
Рассмотрим некую функцию R(x,y,z), заданную в области (V) и на границе, непрерывную в этой |
|
|
|
|
||||
|
|
|
|
(x,y)) |
области и на границе вместе со своими частными производными первого порядка. Рассмотрим |
|
|
|
|
|
|||
|
|
|
|
|||
|
|
|
|
интеграл |
. Спроецируем тело на область D. Возьмём точку |
|
|
|
|
|
|
||
(x,y).
 z
z
(S)
(V)
y
P(x,y,z)
x |
z |
(V)
 y Q(x,y,z)
y Q(x,y,z)
x
Если |
и |
Сделаем то же самое, но с проекцией на оси y и z.
Теперь спроектируем на оси x и z.
Складывая |
эти |
формулы, |
получаем |
формулу |
Остроградского-Гаусса: |
|
|
|
|
|
|
|
|
. Формула сводит интеграл от
объёма к интегралу по границе.
или |
и |
или |
и |
, |
тогда |
. А если  ,
,  и
и 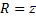 , то:
, то:  .
.
В общем виде теорема звучит так. Пусть в замкнутой ограниченной области (V) заданы функции P(x,y,z), Q(x,y,z) и R(x,y,z), непрерывные на (V)
вместе |
со |
своими |
частными |
производными |
первого |
порядка. |
Тогда |
имеет |
место |
следующее |
тождество: |
|
|
|
|
|
|
|
. |
|
|
|
|
|
(V) |
|
Запись формулы в векторном виде. |
Пусть |
|
. В |
обычном |
виде формула |
выглядит так: |
||
|
|
|
|
|
|
|
|
|
|
|
|
Левую часть можно записать так: 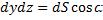 ,
, 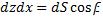 ,
, 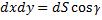 . Следовательно:
. Следовательно:
, так как
 . Мы получили поток вектора через замкнутую поверхность. Правую часть можно
. Мы получили поток вектора через замкнутую поверхность. Правую часть можно
35

записать как дивергенцию (расходимость):  . В итоге формула Гаусса-Остроградского в векторном виде:
. В итоге формула Гаусса-Остроградского в векторном виде:
 . Читается так: поток вектора через замкнутую поверхность равен интегралу по объёму от его дивергенции.
. Читается так: поток вектора через замкнутую поверхность равен интегралу по объёму от его дивергенции.
Дивергенцией векторного поля A в точке M V называется производная функции |
по объему в этой точке: |
.
35. Формула Стокса, ее запись в координатной и векторной (инвариантной) формах.
 .
. 
{ф. Грина}=
=
. Аналогично 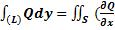 c
c ,
,
 c
c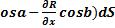 .
.
Теорема: Пусть в некоторой окрестности поверхности S функции Р(х, у, z), Q(x, у, z) и R(x, у, z) непрерывны и имеют непрерывные частные, производные первого порядка. Тогда имеет место следующее соотношение:
 . (Формула Стокса).
. (Формула Стокса).
|
|
|
|
. |
|
|
|
Инвариантная запись формулы Стокса: Используя выражение для |
в ортогональном базисе , |
: |
|
||||
|
|
|
. Укажем на поверхности S определенную сторону, т.е. укажем непрерывное поле |
||||
единичных нормалей |
. Используя стандартное обозначение cos x, cos y, cos z для координат единичного вектора нормали к поверхности S получим: |
||||||
|
|
|
|
. Из соотношения видно, левая часть формулы Стокса может быть |
|||
записана в виде |
|
. Скалярное произведение: |
|
и элемент площади |
поверхности S не зависят от выбора декартовой |
||
прямоугольной системы координат в пространстве, и при переходе к новому ортогональному базису ', |
левая часть формулы не изменит своего |
||||||
значения и формы – инвариантна. |
|
|
|
|
|
|
|
Рассмотрим |
|
. Пусть – единичный вектор касательной в точках границы L поверхности S, cosα, cosβ, cosγ – координаты этого |
|||||
вектора. |
|
, |
. Т.о |
|
|
|
|
|
|
|
|
|
– циркуляция векторного поля p по кривой L. |
- инвариант. |
|
Получаем |
= |
. |
|
|
|
|
|
36
