
- •1*. Определенный интеграл. Интегральная сумма. Верхняя и нижняя интегральные суммы. Их свойства.
- •2**. Ограниченность интегрируемой функции.
- •3**(-). Критерий интегрируемости ограниченной на отрезке функции.
- •4≠. Теорема об интегрируемости монотонной на отрезке, а также непрерывной на отрезке функций.
- •5*. Основные свойства определенного интеграла.
- •6*. Формула среднего значения для определенного интеграла.
- •7. Интеграл с переменным верхним пределом. Его непрерывность и дифференцируемость.
- •8. Формула Ньютона-Лейбница для определенного интеграла.
- •9. Вычисление определенного интеграла по частям и заменой переменной.
- •10. Применение определенного интеграла (площадь плоской фигуры, длина дуги кривой, объем тела вращения).
- •11++. Понятие числового ряда и его суммы. Критерий Коши сходимости ряда. Необходимое условие сходимости.
- •12+. Признаки Даламбера и Коши сходимости рядов с неотрицательными членами.
- •13. Интегральный признак Коши сходимости числового ряда.
- •14++. Знакопеременные числовые ряды. Абсолютная и условная сходимость. Знакочередующиеся ряды. Признак Лейбница.
- •15++. Функциональный ряд. Сумма ряда. Определение равномерной сходимости ряда. Критерий Коши равномерной сходимости функционального ряда.
- •16+. Признак Вейерштрасса равномерной сходимости.
- •17++. Свойства равномерно сходящихся функциональных рядов. Теорема о непрерывности суммы равномерно сходящегося ряда из непрерывных функций. Теорема о почленном интегрировании и дифференцировании ряда (без доказательства).
- •18+-(нет доказательства теоремы). Степенной ряд. Теорема Абеля.
- •19++. Радиус сходимости степенного ряда. Формула Коши-Адамара для радиуса сходимости степенного ряда.
- •20+. Вопрос для консультации – надо ли доказывать? На лекциях Михайлов не доказывал!
- •Кроме того – лучше его переспросить еще раз и саму теорему, так как в его интерпретации она отличается от общепринятой формулировки, в которой требуется только лишь существование всех производных, а вовсе не их ограниченность ≤ n!!!
- •Ряд Тейлора. Теорема Тейлора о разложимости функции в ряд Тейлора. Разложение основных элементарных функций в ряд Тейлора-Маклорена: ex, sinx, cosx, (1+x)a, ln(1+x).
- •21++. Ряд Фурье. Разложение функций: в общий ряд Фурье, в ряд по синусам, в ряд по косинусам.
- •22-. Функции многих переменных. Понятие n-мерного евклидового пространства. Множество точек евклидового пространства. Последовательность точек и ее предел. Определение функции нескольких переменных.
- •23-. Предел функции нескольких переменных. Непрерывность функции. Частные производные.
- •24+--. Определение дифференцируемой функции нескольких переменных и ее дифференциала. Производные и дифференциалы высших порядков.
- •25++?-по Тейлору, у меня нет этой лекции. Формула Тейлора для функции многих переменных. Экстремум функции нескольких переменных. Необходимое условие экстремума. Достаточное условие экстремума.
- •26+. Двойной интеграл и его свойства. Сведение двойного интеграла к повторному.
- •27+. Тройной интеграл, сведение его к повторному.
- •28. Замена переменных в двойном интеграле. Пример: случай полярных координат.
- •29. Замена переменных в тройном интеграле. Цилиндрические и сферические координаты.
- •30. Вычисление площади гладкой поверхности, заданной параметрически и в явном виде.
- •32+нет доказательства!. Формула Грина. Условия независимости криволинейного интеграла от пути интегрирования.
- •33. Поверхностные интегралы первого и второго рода, их основные свойства и вычисление.
- •35. Формула Стокса, ее запись в координатной и векторной (инвариантной) формах.
- •36. Скалярное и векторное поля. Градиент, дивергенция, ротор. Потенциальное и соленоидальное поля.
- •37. Оператор Гамильтона. (набла) его применение (примеры).
- •38. Основные понятия, относящиеся к обыкновенным дифференциальным уравнениям (ОДУ) первого порядка: общее и частное решения, общий интеграл, интегральная кривая. Задача Коши, ее геометрический смысл.
- •39++. Интегрирование ОДУ первого порядка с разделяющимися переменными и однородных.
- •40++. Интегрирование линейных ОДУ первого порядка и уравнения Бернулли.
- •41++. Интегрирование ОДУ первого порядка в полных дифференциалах. Интегрирующий множитель.
- •42++. Дифференциальные уравнения первого порядка, неразрешенные относительно производной. Метод введения параметра.
- •43. Уравнение n-го порядка с постоянными коэффициентами. Характеристическое уравнение. Фундаментальная система решений (ФСР) однородного уравнения, общее решение неоднородного уравнения.
- •44. Система линейных дифференциальных уравнений первого порядка. ФСР однородной системы. Общее решение однородной системы.
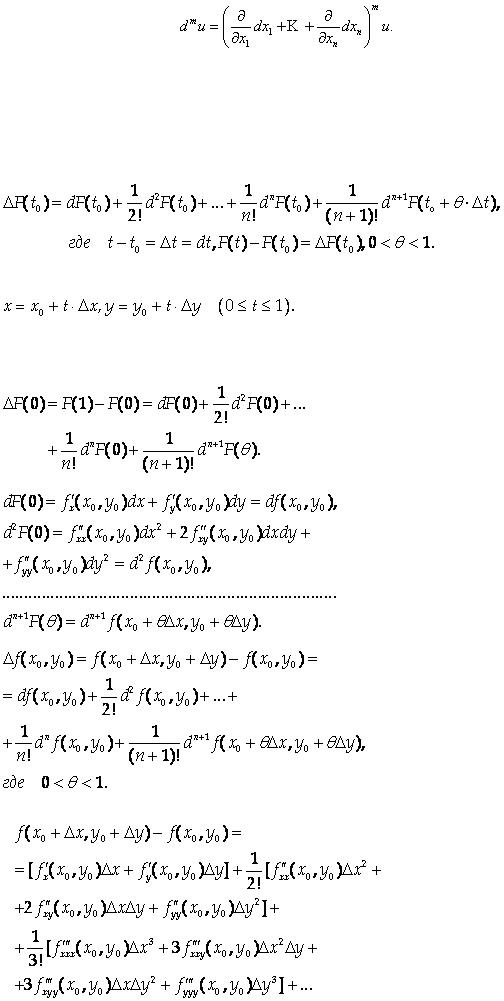
Дифференциал m – го порядка равен
25++?-по Тейлору, у меня нет этой лекции. Формула Тейлора для функции многих переменных. Экстремум функции нескольких переменных. Необходимое условие экстремума. Достаточное условие экстремума.
Как известно, функцию F(T) при условии существования ее производных по порядок N+1 можно разложить по формуле Тейлора с остаточным членом в форме Лагранжа. Запишем эту формулу в дифференциальной форме:
В этой форме формулу Тейлора можно распространить на случай функции нескольких переменных.
Рассмотрим функцию двух переменных F(X, Y), имеющую в окрестности точки (Х0 , у0) непрерывные производные по (N + 1)-й порядок включительно. Зададим аргументам Х И У некоторые приращения DХ и DУ и рассмотрим новую независимую переменную T:
Эти формулы задают прямолинейный отрезок, соединяющий точки (x0 ,у0) и (x0+∆x, у0+∆y). Тогда вместо приращения ∆F(x0,y0) можно рассматривать приращение вспомогательной функции
F(t) = F(x0+t ∆x, y0+t∆y),
Равное ∆F(0) = F(1) – F(0). Но F(t) является функцией одной переменной T, следовательно, к ней применима формула, приведенная в начале раздела. Получаем:
Отметим, что при Линейной замене переменных дифференциалы высших порядков обладают свойством инвариантности, то есть
Подставив эти выражения в предыдущую формулу, получим Формулу Тейлора для функции двух переменных:
Замечание. В дифференциальной форме формула Тейлора для случая нескольких переменных выглядит достаточно просто, однако в развернутом виде она весьма громоздка. Например, даже для функции двух переменных первые ее члена выглядят так:
Максимум и минимум функции нескольких переменных
24
Напомним, что под окрестностью точки плоскости понимается внутренность любого прямоугольника, окружающего эту точку, исключая саму точку (проколотая окрестность).
В пространстве это будет произвольный параллелепипед, содержащий эту точку за вычетом самой точки.
Определение. Максимумом (строгим) функции f(x, y) называется такое значение f(x1, y1) этой функции, которое больше всех ее значений f(x, y), принимаемых данной функцией в точках некоторой окрестности точки О(х1, у1). (Окрестность может быть весьма малой по своим линейным размерам).
Определение. Минимумом (строгим) функции f(x, y) называется такое значение f(x2,y2), которое меньше всех ее значений f(x,y), принимаемых данной функцией в точках некоторой окрестности О(х2, у2).
Максимум или минимум функции f(x, y) называется экстремумом этой функции. Точка, в которой достигается экстремум, называется точкой экстремума (точка минимума, точка максимума).
Аналогично определяется экстремум функции f (x, y, z) и т.д.
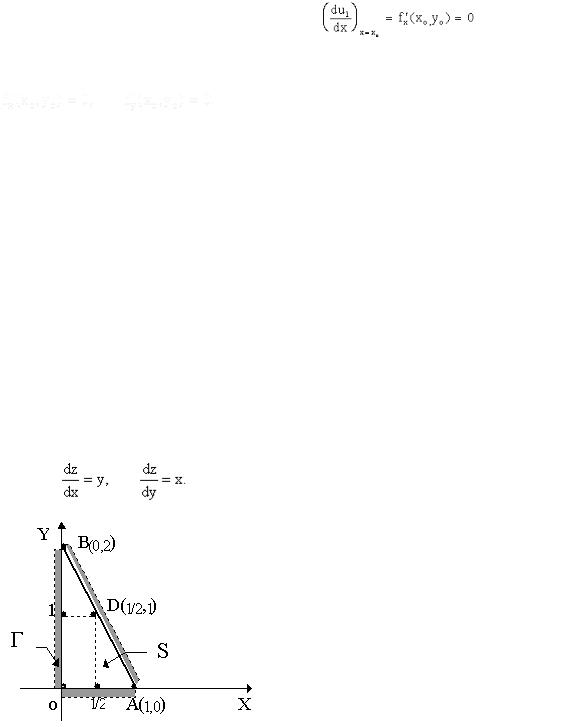
Теорема. (Необходимый признак экстремума функции нескольких переменных). В точке экстремума функции нескольких переменных каждая ее частная производная первого порядка либо равна нулю, либо не существует.
Д о к а з а т е л ь с т в о. Пусть u = f (x, y) и f (x0, y0) - ее максимум (для минимума рассуждения аналогичны). Зафиксируем одну из переменных, например, у, полагая у = у0, тогда получим функцию одной переменной U1 = f (x, yo), которая, очевидно, будет иметь максимум при х = хо. Отсюда,
на основании теории экстремума одной переменной, получаем, что |
или |
не существует. |
|
Пусть теперь у=у0, а х0- фиксируем, тогда |
или не существует. |
|
|
С л е д с т в и е. В точке экстремума М0 (х0, у0) дифференцируемой функции f (x, y) выполнены равенства
Для U = f(x, y, z) в точке Мо (хо ,уо, zо) будет выполнено условие  .
.
З а м е ч а н и е. Точку, в которой частные производные первого порядка либо не существуют, либо равны нулю, называют критической. Т.е. экстремумы функции нескольких переменных могут достигаться лишь в критических точках.
Пример. Покажем, что указанные выше условия не являются достаточными. Пусть z = f(x, y) = x y тогда имеем
Следовательно, |
|
|
Однако точка 0(0,0) не является точкой экстремума, т.к. в любой окрестности точки о,о имеются |
точки |
|
|
|
|
|
и |
|
f(A) = |
2 f(0) |
и f(B) = - 2 f(0). |
|
Абсолютный экстремум
Определение. Наименьшее или наибольшее значение функции в данной области называется абсолютным экстремумом функции. (Соответственно, абсолютный минимум, абсолютный максимум).
Теорема. (Вайерштрасс) Функция, непрерывная в ограниченной и замкнутой области, достигает в этой области своего наименьшего и своего наибольшего значения. (Без доказательства)
Теорема . Абсолютный экстремум функции в данной области достигается либо в критической точке функции, принадлежащей этой области, либо в граничной точке области. (Без доказательства)
Пример. Для функции z = x y найти абсолютный экстремум в треугольной области S с вершинами О(0,0), А(1,0), В(0,2).
Определим
Рис. 15.1.
Критическая точка O(0,0) S. На участке ОА имеем у = 0 (0 х ) и тогда z = 0. Аналогично ОВ: х = 0 (0 у 2) z = 0.
25

Наконец, отрезок АВ имеет уравнение |
или у = 2 - 2х |
(0 х 1). |
|
|
|
|
Отсюда z = x y = 2x - 2x2 . |
|
|
|
|
|
|
Имеем |
, т.е. при |
и т.к. |
, то в точке |
|
функция Z |
достигает своего |
наибольшего значения |
|
на отрезке АВ. |
|
|
|
|
Итак, наименьшее значение |
z в S есть m=0 и оно реализуется в точках отрезков ОВ и ОА, составляющих часть границы Г. |
достигает в |
||||
точке |
|
|
|
|
|
|
Теорема. (достаточное условие экстремума) |
Если дважды дифференцируема в стационарной точке |
, то |
-- точка минимума (максимума), если |
|||
квадратичная форма |
|
положительно (отрицательно) определена. Если эта форма не определена, то экстремума в |
||||
этой точке нет. Если она вырождена, то неизвестно, является ли 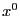 точкой экстремума. Доказательство. По формуле Тейлора приращение функции в точке
точкой экстремума. Доказательство. По формуле Тейлора приращение функции в точке 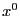 можно записать в виде
можно записать в виде
|
|
|
, поскольку, по необходимому условию экстремума, частные производные будут |
|||||
равны нулю. Перепишем выражение в виде |
|
|
, причем |
при |
. Заметим, что новые переменные |
|||
|
изменяются на единичной сфере, т.к. |
. Кроме того, квадратичная форма |
|
непрерывна и по теореме |
||||
Вейерштрасса на сфере принимает наименьшее значение, обозначим его |
. Пусть форма положительно определена. Тогда |
. Теперь благодаря |
||||||
тому, что |
при |
можно подобрать такое |
, что при |
|
выполнено |
|
, тогда выполнено |
|
доказательство аналогично. |
|
в этой окрестности. Что и означает, что |
|
-- точка минимума. Для точки максимума |
||||
|
|
|
|
|
|
|
||
Замечание . В случае двух переменных матрица квадратичной формы имеет вид |
. Тогда если |
|
, то для положительной определенности |
|||||
достаточно |
|
-- тогда имеется минимум. Если же |
|
, то достигается максимум. Если же |
, то ничего |
|||
сказать нельзя. |
|
|
|
|
|
|
|
|
Лекция Михайлова от 16.04.15:
Точка M0(x0,y0) называется точкой максимума, если в некоторой окрестности этой точки f(x0,y0)≥f(x.y). (Если f(x0,y0)>f(x.y), то строгий максимум.)
Точка M0(x0,y0) называется точкой минимума, если в некоторой области этой точки f(x0,y0)≤f(x.y). Строгий минимум при строгом <. Необходимое условие экстремума дифференцируемой функции: ∂f|M=M0=0, т.е. все частные производные в точке экстремума (M0) равны нулю.
Достаточное условие экстремума:
f df |
|
|
|
d 2 f |
|
|
d 3 f |
|
|
d n f |
Rn 1 - приращение, через ф-лу Тейлора |
|
|
|
|||||||||
|
|
2! |
|
3! |
|
n! |
|||||
|
M M 0 |
M M 0 |
|
M M 0 |
|
M M 0 |
|||||
|
|
|
|
|
|
|
|
|
|||
Если df|M=M0=0, то точка M0 называется точкой возможного экстремума при этом приращении функции |
|||||||||||
f d 2 f |
|
|
o 2 |
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
||||
2! |
|
M M 0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
∆f=f(x,y) – f(x0,y0) < 0 – максимум
∆f > 0 – минимум.
Т.е. наличие и характер экстремума в М0 определяется знаком второго дифференциала.
d 2 f |
|
2 f |
|
dx2 2 |
2 f |
|
|
|
dxdy |
2 f |
|
dy2 A dx2 2B dxdy C dy2 |
|||||||||
|
|
|
|
||||||||||||||||||
|
|
|
|
|
2 |
|
|||||||||||||||
|
|
|
|
M M 0 |
|
x |
2 |
|
|
x y |
|
|
|
|
y |
|
|
||||
|
|
|
|
|
|
M M 0 |
|
M M 0 |
|
|
|
M M 0 |
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
f |
A x |
2 |
B x y C y |
2 |
2 |
|
|
x 2 |
2B |
x |
|
||||||||
|
|
|
y |
A |
|
|
C |
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
y |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
y |
|
|
|
|
Знак второго дифференциала, а следовательно и приращения функции ∆f определяется знаком квадратного трехчлена:
A x 2y
2B x C , а именно, если A>0 и D=B2-AC<0 – минимум, если A<0 и D<0 – минимум. Если D≥0 – экстремума нет.
y
26+. Двойной интеграл и его свойства. Сведение двойного интеграла к повторному.
y |
Определение двойного интеграла. Пусть на плоскости XY задана функция z=f(x,y) и область (P) (область задания |
||
функции f(x,y)), её площадь P. Произведём разбиение площади сеткой кривых Pi, где Pi – частичная область. Внутри |
|||
|
|||
|
частичной области возьмём произвольную точку с координатами (ξi,ηi). Составим интегральную сумму: |
||
|
(P) |
|
|
|
. Пусть λ – характеристика разбиения, которая равна |
, где di – диаметр |
|
x |
26 |
|
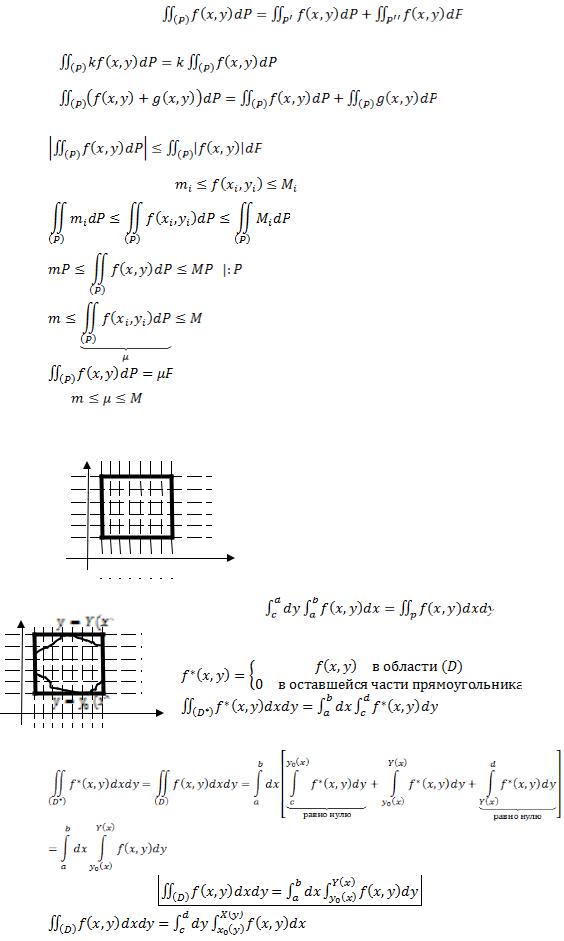
частичной области. Диаметр – максимальное расстояние между любой парой точек в области. Устремим λ к нулю. Если существует предел интегральных
сумм 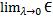 , то этот предел и называется двойным интегралом:
, то этот предел и называется двойным интегралом: 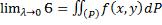 . Основные свойства двойного интеграла:
. Основные свойства двойного интеграла:
Свойство аддитивности: Свойства линейности:
а)
б)
Модуль интеграла меньше или равен интегралу от модуля:
Теорема о среднем. Так как
Где
Сведение двойного интеграла к повторному.
y
d
c
a |
|
|
|
|
|
|
|
b |
x |
|
|
|
|
|
|
|
|
то, проинтегрировав это неравенство, получим:
Теорема. Если функция f(x, y) интегрируема в прямоугольнике, указанном на рисунке, и если 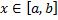 и существует интеграл
и существует интеграл 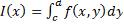 , тогда существует повторный интеграл
, тогда существует повторный интеграл 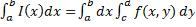 и он равен двойному:
и он равен двойному: 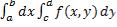 =
= 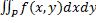 .
.
Замечание. Если f(x, y) интегрируема в прямоугольнике, указанном на рисунке, и  и
и
существует интеграл 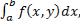 тогда существует повторный интеграл
тогда существует повторный интеграл
y
d
|
(D) |
|
|
c |
b |
x |
|
a |
|||
|
|
.
Предположим, что область D произвольного вида. Делаем разбиение и проводим параллельные линии. Заключим область (D) в прямоугольник (D*), 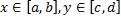 , и в нём определим функцию f*(x,y):
, и в нём определим функцию f*(x,y):
.
Формула в общем виде: |
. Так же доказывается, что |
27
