Добавил:

zex713 Опубликованный материал нарушает ваши авторские права? Сообщите нам.

Вуз:

Национальный исследовательский ядерный университет (МИФИ)

Предмет:

Дифференциальное и интегральное исчисление

Файл:

Ekzamen_Integraly_2015v1.pdf

Скачиваний:

113

Добавлен:

25.06.2015

Размер:

1.99 Mб

Скачать

☆

<<< < Предыдущая 1 2 34 / 114 5 6 7 8 9 10 11 > Следующая >>>

Определение. Частными (частичными) суммами функционального ряда			называются функции
Определение. Функциональный ряд		называется сходящимся в точке (х=х0), если в этой точке сходится последовательность его частных сумм.
Предел последовательности		называется суммой ряда	в точке х0.
Определение. Совокупность всех значений х, для которых сходится ряд			называется областью сходимости ряда.
Определение. Ряд	называется равномерно сходящимся на отрезке [a,b], если равномерно сходится на этом отрезке последовательность частных
сумм этого ряда.
Теорема. (Критерий Коши равномерной сходимости ряда)
Для равномерной сходимости ряда		необходимо и достаточно, чтобы для любого числа ε>0 существовал такой номер N(ε), что при n>N и любом

целом p>0 неравенство |un+1(x)+un+2(x)+ … + un+p(x)| < ε выполнялось бы для всех х на отрезке [a,b].

16+. Признак Вейерштрасса равномерной сходимости.

Признак Вейерштрасса (достаточный признак равномерной сходимости ф. ряда):

Если числовой ряд с неотрицательными членами an сходится, и для членов функционального ряда n 1


un x при всех n и всех	x X ,
n 1

выполняется	un x		an , то ряд сходится абсолютно и равномерно в области X.
выполняется	un x		an , то ряд сходится абсолютно и равномерно в области X.

Говорят в этом случае, что числовой ряд an				«мажорирует» исходный функциональный ряд, а сам числовой ряд называют мажорантным.
			n 1
Существует простой признак для проверки равномерной сходимости (принак Вейерштрасса)
Можно рассматривать			и при этом сохраняется терминология числовых рядов, связанная с абсолютной и условной сходимостью.
Как и в рядах, абсолютная сходимость сильнее сходимости: из абсолютной сходимости вытекает сходимость.
Теорема (Вейерштраса):
,		,		— сходится. Тогда	равномерно сходится на .

Доказательство:

Применим критерий Коши:

Сопоставляя с предыдущим неравенством, которое верно ,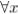

. Тогда, по критерию Коши, ряд равномерно сходится.

17++. Свойства равномерно сходящихся функциональных рядов. Теорема о непрерывности суммы равномерно сходящегося ряда из непрерывных функций. Теорема о почленном интегрировании и дифференцировании ряда (без доказательства).

Общие свойства функциональных рядов


О п р е д е л е н и е. Ряды	u1(x)+u2(x)+ … + un(x) + … = un (x) , (24)
	n 1

члены которых являются функциями от х, называются функциональными. Предполагается, что все функции un(x) определены и непрерывны в одном и том же интервале, конечном или бесконечном.

Ряд (24) может сходиться для одних значений х и расходиться для других.

Значение х = х0, при котором получающийся из (24) числовой ряд un (x0 ) (25)

n 1

сходится, называется точкой сходимости ряда (24). Совокупность всех точек сходимости ряда называется областью сходимости ряда. Областью сходимости функционального ряда обычно бывает какой-нибудь промежуток оси Ох. Говорят, что ряд (24) сходится в этой области.

Сумму n первых членов ряда (n-ю частичную сумму) обозначают через Sn(x) , а остаток ряда обозначают через Rn(x). Функциональный ряд сходится при некотором значении х, если существует конечный предел

S(x) – сумма функционального ряда. Ее можно представить в виде S(x) = Sn(x) + Rn(x). Каждому значению х из области сходимости Х соответствует определенное значение S(x).

Равномерная сходимость ряда О п р е д е л е н и е. Функциональный ряд (24) называется равномерно сходящимся в некоторой области Х, если для любого сколь угодно малого числа ε >

0 можно указать такое целое число N(ε) > 0, зависящее только от ε и не зависящее от х, что при всех n > N(ε) неравенство |Rn(x)| < ε выполняется для всех х из области Х.

Достаточный признак равномерной сходимости функционального ряда – признак Вейерштрасса

Если члены функционального ряда (24) u1(x), u2(x),u3(x),…, un(x)… в некоторой области Х по абсолютной величине не превосходят соответствующих

членов некоторого сходящегося числового ряда с положительными членами	, то функциональный ряд

u1(x)+u2(x)+ … + un(x) + … = un (x) , в этой области сходится равномерно.
n 1
Это значит, что во всех точках области Х должно выполняться неравенство	, (n = 1, 2, 3, …).


Ряд an называется мажорантным (усиливающим) по отношению к ряду (24).
n 1
Свойства равномерно сходящихся функциональных рядов:

1. Сумма S(x) равномерно сходящегося ряда un (x) в области Х, где un(x) (n = 1, 2, 3, …) - непрерывные функции, является непрерывной функцией
n 1
в области Х.

2. Равномерно сходящийся ряд un (x) , где un(x) (n = 1, 2, 3, …) -непрерывные функции, можно почленно интегрировать, т.е. справедливо
n 1
равенство
. (26)
3. Если ряд

u1(x)+u2(x)+ … + un(x) + … = un (x) , составленный из функций, имеющих непрерывные производные	,

n 1

сходится в области C и его сумма равна S(x), а ряд из производных

равна сумме ряда из производных:

S′(x) = u′1(x)+u′2(x)+ … + u′n(x) + … = u (x) (27) n

n 1

u (x) сходится в этой области равномерно, то производная суммы ряда S′(x) n

n 1

Коротко эту теорему формулируют так:

Если ряд, составленный из производных сходящегося ряда (27), сходится равномерно, то исходный ряд (24) можно почленно дифференцировать.

Отметим: здесь не предполагаются равномерная сходимость исходного ряда, а также дифференцируемость его суммы; они следуют из условий теоремы.

Однако проверка равномерной сходимости ряда

оказаться неприменимой).

u (x) является обязательной; при невыполнении этого теорема может потерять смысл (т.е. n

n 1

18+-(нет доказательства теоремы). Степенной ряд. Теорема Абеля.

Важным случаем функциональных рядов являются степенные ряды:


c0 c1x c2 x2 cn xn cn xn				(13)
или		n 0
или
c0 c1 x x0 c2 x x0 2
c0 c1 x x0 c2 x x0 2	cn x x0 n cn x x0		n
		n 0
Для выяснения свойств степенных рядов достаточно ограничиться рассмотрением рядов вида (13), так как ряд по степеням x					x0 легко свести к
виду (13) заменой переменных x	x0	~		x0.
виду (13) заменой переменных x	x0	x , т.е. переносом начала координат в точку		x0.

Для выяснения характера области сходимости степенного ряда сформулируем следующую теорему:

Теорема 6.1. (Абеля):

Пусть степенной ряд (13) сходится в точке x0 0. Тогда он сходится абсолютно для всех х, таких, что

, и равномерно в любой области

Следствие: Если степенной ряд (13) расходится в точке x1, то он расходится и во всех точках x таких, что x x1 .

Для определения области сходимости степенного ряда используется либо признак Даламбера, либо признак Коши. Рассмотрим степенной ряд:

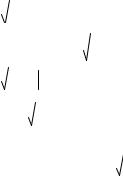
cn x n

(14)

n 0

Вычислим предел:

lim

cn 1 x n 1

lim

cn 1

.(15)

cn x n

L 1 , и расходится, если

L 1 . Следовательно, ряд (14) сходится абсолютно,

Если существует предел (15), то ряд (14) сходится, если

если

lim

cn 1

lim

и расходится, если

lim

cn 1

Определение:

Число

, такое, что для всех x, удовлетворяющих условию

R ряд (13) сходится, а для всех х удовлетворяющих условию

ряд расходится, называется радиусом сходимости ряда.

Формула для радиуса сходимости, получаемая с помощью признака Даламбера, имеет вид

lim

(16)

cn 1

Область сходимости ряда - так называют множество точек сходимости функционального ряда, т.е. множество значений аргумента х, для которых ряд (бесконечная сумма)

сходится Пример 6.1.

Найти область сходимости ряда Область сходимости ряда



	n!	x n при a 1 .
	2	x n при a 1 .
n 1 a n
По признаку Даламбера:
R lim			n !a n 1 2	lim	a 2n 1	,
R lim				lim		,
	n n 1 !a n2			n n 1

что означает, что ряд сходится на всей оси Х.

19++. Радиус сходимости степенного ряда. Формула Коши-Адамара для радиуса сходимости степенного ряда.

Из т. Абеля следует, что степенной ряд сходится в области |x-x0| < R, которая называется радиусом сходимости. Найдем этот радиус.

Применим признак Коши сходимости числового ряда:

lim n

1=> ряд сходится,

un = an( x - x0)n => lim n

an x x0 n

lim n

x x

L lim n

, тогда ряд сходится в области

x x

Следовательно, радиус сходимости степенного ряда определяется формулой:

ãäå

L lim n

(формула Коши – Адамара)

Итак, в своей области сходимости степенной ряд сходится к некоторой функции f(x), т.е. f (x) an x x0

n 0

20+. Вопрос для консультации – надо ли доказывать? На лекциях Михайлов не доказывал!

Кроме того – лучше его переспросить еще раз и саму теорему, так как в его интерпретации она отличается от общепринятой формулировки, в которой требуется только лишь существование всех производных, а вовсе не их ограниченность ≤ n!!!

Ряд Тейлора. Теорема Тейлора о разложимости функции в ряд Тейлора. Разложение основных элементарных функций в ряд Тейлора-Маклорена: ex, sinx, cosx, (1+x)a, ln(1+x).

(Формулировка с лекции Михайлова от 26.03.15 будет ниже).

Пусть функция

бесконечно дифференцируема в некоторой окрестности точки . Формальный ряд

называется рядом Тейлора функции 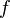в точке .

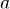В случае, если 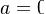, этот ряд также называется рядом Маклорена.

Пусть

. Тогда ряд

называется рядом Тейлора функции

в точке

Если		, то	по формуле Тейлора:
, где		- остаточный член формулы Тейлора, т.е.			, где	- n-ая
частичная сумма ряда Тейлора функции			в точке	ряд Тейлора сходится на	тогда и только тогда,
когда
Пусть		и			, тогда на
Доказательство:
			, где	- остаточный член формулы Тейлора в форме Лагранжа:
					.
Рассмотрим ряд		,		по признаку Даламбера ряд сходится		. Перейдем к пределу
при	в неравенстве
			на	.

Теорема Тейлора

Пусть функция f(x) имеет в точке х = а и некоторой ее окрестности производные порядка до (n+1) включительно.{Т.е. и все предыдущие до порядка n функции и их производные непрерывны и дифференцируемы в этой окрестности}.

Пусть х - любое значение из этой окрестности, но а х Тогда между точками х и а найдется такая точка , что справедлива формула:

это выражение называется формулой Тейлора, а выражение:

называется остаточным членом в форме Лагранжа.

<<< < Предыдущая 1 2 34 / 114 5 6 7 8 9 10 11 > Следующая >>>

Соседние файлы в предмете Дифференциальное и интегральное исчисление

#
25.06.201515.97 Mб113Ekzamen_Integraly_2015v1.doc
#
25.06.20151.99 Mб113Ekzamen_Integraly_2015v1.pdf
#
25.06.2015109.62 Кб49Minimum_po_integrallam.pdf
#
25.06.2015106.53 Кб47minimum_znaniy-1.docx
#
19.06.2015106.53 Кб30minimum_znaniy.docx
#
19.06.201515.73 Mб275otveti.doc
#
23.06.2015202.75 Кб25V2_Kr10int.doc