22. Предел функции нескольких переменных. Непрерывность функции. Частные производные.

Определение. Число А называется пределом функции f(M), где М(x1,x2,…xn) – точка n-мерного пространства, при стремлении точки М к точке М0(x10,x20,…xn0) любым образом, если для всякого сколь угодно малого >0 существует такое число>0, что из условия<, где- расстояние между точками М и М0, следует<.

Обозначается:

А .

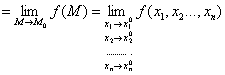Пусть z=f(x,y). Придадим x и y приращения и. Получим приращениефункции z=f(x,y). Если

                        ,                                                                                   (1)

 т.е. бесконечно малым аргументам соответствует бесконечно малое приращение функции, то говорят, что функция непрерывна.

Распишем x0+y+-f(x0,y0) и положим x0+x=x,y0+,то выражение(1) можно записать в виде

                        f(x,y)=f(x 0,y0),                                                                      (2)

т.е. непрерывность функции означает, что ее предел равен ее значению от пределов аргументов.

 Функция, непрерывная в каждой точке некоторой области, называется непрерывной в области. Если в некоторой точке не выполняется условие (2), то эта точка называется точкой разрыва.

Частные производные.

Пусть z=f(x,y). Зафиксируем какую-либо точку (x,y), а затем, не меняя закрепленного значения аргумента y, придадим аргументу x приращение . Тогда z получит приращение, которое называется частным приращением z по x и обозначаетсяи определяется формулой.

Аналогично, если x сохраняет постоянное значение, а y получает приращение , то z получает частное приращение z по y,.

Определение. Частной производной по x от функции z=f(x,y) называется предел отношения частного приращения по x к приращениюпри стремлениик нулю, т.е.

Частная производная обозначается одним из символов.

Аналогично определяется частная производная по y:

                                 .

Таким образом, частные производные функции двух переменных вычисляются по тем же правилам, что и производные функции одного переменного.

Пример. Найти частные производные функции z=x2e x-2y.

Решение.

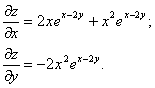
Частные производные функции любого числа переменных определяются аналогично.

            4. Геометрическая интерпретация частных

               производных функции двух переменных

 

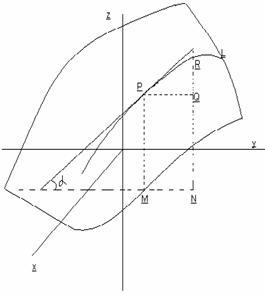
Пусть уравнение z=f(x,y) –это уравнение поверхности. Проведем плоскость x=const.  L- линия пересечения поверхности с плоскостью x=const. При данном x на плоскости ХОУ возьмем точку М. На поверхности z=f(x,y) ей соответствует точка Р(x,y,z). Дадим переменному y приращение Тогда функция z получит приращениеОтношениеравно тангенсу угла, образованного секущей RР с положительным направлением оси ОУ,

Итак, частная производная численно равна тангенсу угла

наклона касательной к кривой, получающейся в сечении поверхности z=f(x,y) плоскостью x=const.

 Аналогично, частная производная численно равна тангенсу угла наклона касательной к кривой, получающейся в сечении поверхности z=f(x,y) плоскостью x=const.

23. Определение дифференцируемой функции нескольких переменных и ее дифференциала. Производные и дифференциалы высших порядков.

Производные ФНП.

Рассмотрим функцию u = F(x), определенную в некоторой области D. Пусть − фиксированная точка. Дадим координате х1 приращение. Если существует конечный предел, то он называется частной производной функции F(x) по переменной х1 и обозначается

Аналогично определяются частные производные по всем остальным переменным.

Замечания.

1. Частная производная по какой либо переменной есть обычная производная, при условии, что все остальные переменные – константы.

2. Последнее обозначение, в отличие от функций одной переменной, не равно частному от деления двух дифференциалов, а является неразрывным символом.

В частном случае двух переменных частная производная равна тангенсу наклона касательной к сечению поверхности плоскостью, перпендикулярной ко второй переменной.

Примеры.

 

Частные производные высших порядков.

Вычисляя частные производные ФНП, мы снова получаем функцию тех же переменных, от которой можно взять частную производную, в том числе и по другой переменной (если она, конечно, существует): Частные производные по одной и той же переменной называются повторными, а по различным переменным – смешанными. Например:

Примеры.

Теорема 1 (О равенстве смешанных производных). Пусть функция z = f(x,y) имеет вторые частные производные в окрестности т. М0 , непрерывные в самой точке М0.

В этом случае

{Рассмотрим функции

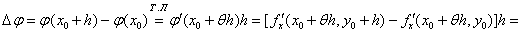
Для аналогично получаем:

Из равенства следует

. Устремив h к нулю , в силу непрерывности производных, получаем: }

Если u = u(x1,…,xn), то все вторые частные производные можно записать с помощью

.

Из т.1 следует, что матрица Гессе – симметрична.

 

Дифференциал ФНП.

Пусть функция u = F(x) определена в области D и − фиксированная точка. Дадим приращение каждому аргументу хţ :Величинубудем называть вектором приращения. В свою очередь функция u получит приращение равное

Определение 1. Функция u = F(x) называется дифференцируемой в т. х , если ее приращение может быть представлено в следующем виде:

где

Aţ = Aţ(x) и не зависит от Δх, а − бесконечно малая при

Величина вектора Δх равна:

Используя это обозначение, можно написать

Легко показать, что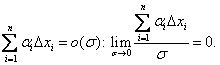

{}

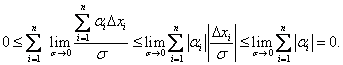Определение 2. Главная и линейная часть приращения дифференцируемой функции называется дифференциалом:

Теорема 1. Функция, дифференцируемая в т. хo − непрерывна в этой точке. {}

Теорема 2. (Необходимое условие дифференцируемости) Если F(x) дифференцируема в т. х , то она имеет все частные производные в этой точке, причем

{Пусть }

Отсюда, Если х − независимая переменная, тои окончательно

Теорема 3. (Достаточное условие дифференцируемости) Пусть F(x) имеет все частные производные в окрестности т. хо , непрерывные в самой этой точке. Тогда функция дифференцируема в т. хо .

{без доказательства}

Замечание. Для дифференцируемости функции одной переменной достаточно существования производной.

Дифференциал функции u называют полным дифференциалом.

Определение 3. Выражение называется дифференциальной формой.

Теорема 4. Дифференциальная форма является полным дифференциалом некоторой функции u(х,у) тогда и только тогда, когда выполнено условие

{1.Необх.: Тогда

2. Дост. – без доказательства}

Пример. Найти общее решение дифференциального уравнения:

 

Геометрический смысл дифференцируемости. Касательная плоскость и нормаль к поверхности.

Рассмотрим поверхность S: z = f(x,y), дифференцируемую в т. S.

Определение 1. Плоскость, проходящая через т. М0 , называется касательной плоскостью к поверхности S в т.М0 , если угол между ней и секущей (М0М1) () стремится к нулю при.

Определение 2. Вектор, ортогональный к касательной плоскости в т.М0 , называется нормальным вектором к поверхности в этой точке. Нормалью к поверхности называется

прямая, проходящая через т.М0 перпендикулярно касательной плоскости в этой точке.

Обозначим ,. Вектор приращения:

Из условия дифференцируемости функции z следует, что

Рассмотрим плоскость и угол φ между секущей и этой плоскостью:приОтсюда сразу следует, что плоскость П – касательная к поверхности в т.М0. В результате имеем:

Функция z = f(x,y), дифференцируемая в некоторой точке (х0,у0) имеет в соответствующей т.М0 касательную плоскость: и нормальный вектор

Пример.

 

Дифференциалы высших порядков.

Определение 1. Дифференциал от первого дифференциала функции называется вторым дифференциалом: Аналогично определяются дифференциалы более старших порядков.

Вычислим второй дифференциал функции двух переменных . При этом будем считать, что дифференциалы независимых переменных dx и dy – величины постоянные (т.е. не зависят от т.(х,у) и не меняются при вычислении каждого последующего дифференциала).

.

Не трудно видеть, что второй дифференциал представляет собой квадратичную форму от

переменных dx и dy. Матрица этой квадратичной формы есть матрица Гессе, т.е.

d2z = (dx,dy)Г(dx,dy)T (см. раздел «Линейная алгебра», квадратичные формы). Кроме того,

второй дифференциал можно записать в символическом виде:

Можно показать, что в общем случае дифференциал 2 – го порядка функции u = F(x) равен

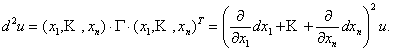
Дифференциал m – го порядка равен