35. Оператор Гамильтона. (набла) его применение (примеры).

Оператор набла (оператор Гамильтона) – векторный дифференциальный оператор, обозначаемый символом . Для трёхмерного евклидова пространства в прямоугольных декартовых координатах оператор набла определяется следующим образом:

Для трёхмерного евклидова пространства в прямоугольных декартовых координатах. оператор набла определяется следующим образом:

,

где — единичные векторы по осям x, y, z.

Через оператор набла естественным способом выражаются основные операции векторного анализа: grad (градиент), div (дивергенция), rot (ротор), а также оператор Лапласа (см. ниже). Широко употребляется в описанном смысле в физике и математике (хотя иногда графический символ используется также для обозначения некоторых других, хотя в некотором отношении не совсем далеких от рассмотренного, математических объектов, например, ковариантной производной).

Под n-мерным оператором набла подразумевается вектор с компонентами в n-мерном пространстве.

36. Основные понятия, относящиеся к обыкновенным дифференциальным уравнениям (оду) первого порядка: общее и частное решения, общий интеграл, интегральная кривая. Задача Коши, ее геометрический смысл.

Дифференциальным уравнением называется соотношение , в котором x – независимая переменная, y – искомая функция. Это обыкновенное дифференциальное уравнение (ОДУ) первого порядка.

– уравнение, разрешённое относительно производной.

f(x,y) – заданная, непрерывная в некоторой области D переменных (x,y) функция.

Пусть. График функцииназывается интегральной кривой,– изоклины кривые.

Пусть правая часть уравнения (*) не зависит от y, то есть , тогда.

На рисунке представлено семейство интегральных кривых, зависящих от одного параметра C.

Пусть . Будем считать независимой переменной y, а x – функция от y, то есть. Тогда. Но еслии это уравнение имеет корень, то добавляется решение, которое надо добавить к общему семейству, зависящему от параметра C.

Всякая функция вида при подстановке в (*), после чего (*) становится тождеством, является решением (общим решением дифференциального уравнения (*)).

Если C взято равным конкретному числу, то решение φ(x,C0) называется частным решением уравнения (*). - отсюда находится значение C.

Условие Коши – когда указано, какому x0 соответствует y0. Задача Коши:– условие уравнения + условие Коши, то есть. Задачу Коши геометрически можно сформулировать так: среди всех интегральных кривых уравнения (*) найти ту кривую (рисунок слева), которая проходит через заданную точку (x0, y0).

Пример. Дано: и. Решить задачу Коши.

Когда , то:

– частное решение задачи Коши.

37. Интегрирование оду первого порядка с разделяющимися переменными и однородных.

Уравнением с разделенными переменными называется дифференциальное уравнение вида: с непрерывными функциями f(х) и g(y). Равенство, где C — произвольная постоянная, определяет общий интеграл уравнения с разделёнными переменными.

Принцип решения таких уравнений:

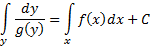
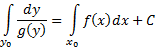
Если дано условие Коши, то есть и, то. Еслии уравнение имеет корень, то это решение добавляется к основному семейству.

Определение однородной функции. Функция f(x,y) называется однородной функцией своих переменных x и y, если, каково бы ни было число , выполняется следующее:, где p – степень (показатель) однородности. Например,– однородная функция, степень однородности, так как. Степень p может быть равной нулю, если.

Уравнение называется однородным, если функция, стоящая в правой части, является однородной функцией своих переменных. Пусть f(x,y) будет однородной функцией степени 0, то есть. Пусть, тогда. Уравнения такого типа решаются заменой (переходом к новой функции):.

– общее решение.

Если , а, то:

Если , то уравнениеимеет корень u0, тогда:– решение:– прямая наряду с семейством.

Общий вид однородного уравнения, если его записать в виде дифференциалов:

То есть M(x,y) и N(x,y) должны быть однородными функциями одной и той же степени однородности.