15. Функциональный ряд. Сумма ряда. Определение равномерной сходимости ряда. Критерий Коши равномерной сходимости функционального ряда.

Определение. Ряд, члены которого являются функциями, называется функциональным рядом. Его обозначают:

(1)

Определение. Если при ряд (1) сходится, тоназывается точкой сходимости ряда (1).

Определение. Множество всех значений , при которых функциональный ряд сходится, называется областью сходимости этого ряда.

Очевидно, что в области сходимости функционального ряда его сумма является функцией от . Будем ее обозначать.

—n-ная частичная сумма.

Ряд называется сходящимся равномерно, если последовательность его частичных сумм сходится равномерно.

Функциональный ряд называется равномерно сходящимся в некоторой области Х, если для любого сколь угодно малого числа > 0 можно указать такое целое число N() > 0, зависящее только от e и не зависящее от х, что при всех n > N() неравенствовыполняется для всех х из области Х.

Свойства равномерно сходящихся рядов.

1. Сумма S(x) равномерно сходящегося ряда 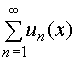в области Х, где un(x) (n = 1, 2, 3, …) - непрерывные функции, является непрерывной функцией в области Х.

2. Равномерно сходящийся ряд , где un(x) (n = 1, 2, 3, …) -непрерывные функции, можно почленно интегрировать, т.е. справедливо равенство

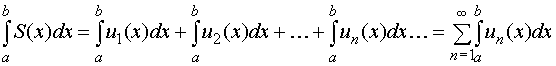. (26)

3. Если  ряд 

 ,

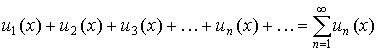составленный из функций, имеющих непрерывные производные , сходится в области C и его сумма равна S(x), а ряд из производныхсходится в этой области равномерно, то производная суммы рядаравна сумме ряда из производных:

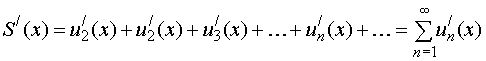. (27)

Определение. Частными (частичными) суммами функционального ряда называются функции

 

Определение. Функциональный ряд называется сходящимся в точке (х=х0), если в этой точке сходится последовательность его частных сумм. Предел последовательностиназывается суммой рядав точке х0.

Определение. Совокупность всех значений х, для которых сходится ряд называется областью сходимости ряда.

 

  Определение. Ряд называется равномерно сходящимся на отрезке [a,b], если равномерно сходится на этом отрезке последовательность частных сумм этого ряда.

 

  Теорема. (Критерий Коши равномерной сходимости ряда)

  Для равномерной сходимости ряда необходимо и достаточно, чтобы для любого числа e>0 существовал такой номер N(e), что при n>N и любом целом p>0 неравенство

выполнялось бы для всех х на отрезке [a,b].

16. Признак Вейерштрасса равномерной сходимости.

Признак Вейерштрасса:

Если числовой ряд с неотрицательными членами сходится и для членов функционального рядапри всехи всехсправедливы оценки

,

то ряд сходится абсолютно и равномерно в области

Говорят в этом случае, что числовой ряд «мажорирует» исходный функциональный ряд, а сам числовой ряд называют мажорантным.

Существует простой признак для проверки равномерной сходимости(принак Вейерштрасса)

Можно рассматривать  и при этом сохраняется терминология числовых рядов, связанная с абсолютной и условной сходимостью.

Как и в рядах, абсолютная сходимость сильнее сходимости: из абсолютной сходимости вытекает сходимость.

Теорема (Вейерштрасс):

, ,  — сходится. Тогда  равномерно сходится на .

Доказательство:

Применим критерий Коши:

Сопоставляя с предыдущим неравенством, которое верно ,

. Тогда, по критерию Коши, ряд равномерно сходится.

17. Свойства равномерно сходящихся функциональных рядов. Теорема о непрерывности суммы равномерно сходящегося ряда из непрерывных функций. Теорема о почленном интегрировании и дифференцировании ряда (без доказательства).

Общие свойства функциональных рядов

О п р е д е л е н и е. Ряды

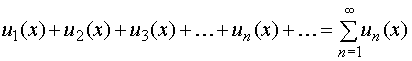, (24)

члены которых являются функциями от х, называются функциональными. Предполагается, что все функции u_n(x) определены и непрерывны в одном и том же интервале, конечном или бесконечном.

Ряд (24) может сходиться для одних значений х и расходиться для других. Значение х = х₀, при котором получающийся из (24) числовой ряд

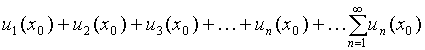(25)

сходится, называется точкой сходимости ряда (24). Совокупность всех точек сходимости ряда называется областью сходимости ряда. Областью сходимости функционального ряда обычно бывает какой-нибудь промежуток оси Ох. Говорят, что ряд (24) сходится в этой области.

Сумму n первых членов ряда (n-ю частичную сумму) обозначают через S_n(x) , а остаток ряда обозначают через R_n(x). Функциональный ряд сходится при некотором значении х, если существует конечный предел

и .

S(x) – сумма функционального ряда. Ее можно представить в виде S(x) = S_n(x) + R_n(x). Каждому значению х из области сходимости Х соответствует определенное значение S(x).

Равномерная сходимость ряда

О п р е д е л е н и е. Функциональный ряд (24) называется равномерно сходящимся в некоторой области Х, если для любого сколь угодно малого числа > 0 можно указать такое целое число N() > 0, зависящее только от e и не зависящее от х, что при всех n > N() неравенство выполняется для всех х из области Х.

Достаточный признак равномерной сходимости функционального ряда – признак Вейерштрасса

Если члены функционального ряда (24) u₁(x), u₂(x),u₃(x),…, u_n(x)… в некоторой области Х по абсолютной величине не превосходят соответствующих членов некоторого сходящегося числового ряда с положительными членами 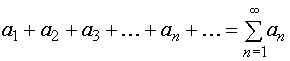, то функциональный ряд

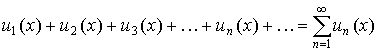
в этой области сходится равномерно.

Это значит, что во всех точках области Х должно выполняться неравенство , (n = 1, 2, 3, …). Ряд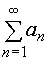называется мажорантным (усиливающим) по отношению к ряду (24).

Свойства равномерно сходящихся функциональных рядов

1. Сумма S(x) равномерно сходящегося ряда 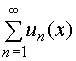в областиХ, где u_n(x) (n = 1, 2, 3, …) - непрерывные функции, является непрерывной функцией в области Х.

2. Равномерно сходящийся ряд 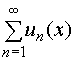, гдеu_n(x) (n = 1, 2, 3, …) -непрерывные функции, можно почленно интегрировать, т.е. справедливо равенство

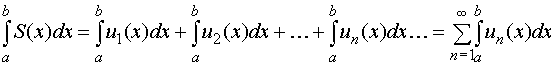. (26)

3. Если  ряд 

 ,

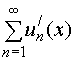составленный из функций, имеющих непрерывные производные , сходится в области C и его сумма равнаS(x), а ряд из производных сходится в этой области равномерно, то производная суммы рядаравна сумме ряда из производных:

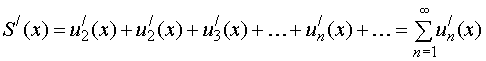. (27)

Коротко эту теорему формулируют так:

Если ряд, составленный из производных сходящегося ряда (27), сходится равномерно, то исходный ряд (24) можно почленно дифференцировать.

Отметим: здесь не предполагаются равномерная сходимость исходного ряда, а также дифференцируемость его суммы; они следуют из условий теоремы. Однако проверка равномерной сходимости ряда 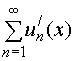является обязательной; при невыполнении этого теорема может потерять смысл (т.е. оказаться неприменимой).