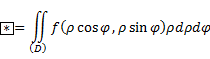- •1. Определенный интеграл. Интегральная сумма. Верхняя и нижняя интегральные суммы. Их свойства.
- •2. Ограниченность интегрируемой функции.
- •Доказательство
- •3. Критерий интегрируемости ограниченной на отрезке функции.
- •4. Теорема об интегрируемости монотонной на отрезке, а также непрерывной на отрезке функций.
- •5. Основные свойства определенного интеграла.
- •6. Формула среднего значения для определенного интеграла.
- •7. Интеграл с переменным верхним пределом. Его непрерывность и дифференцируемость.
- •8. Формула Ньютона-Лейбница для определенного интеграла.
- •9. Вычисление определенного интеграла по частям и заменой переменной.
- •10. Применение определенного интеграла (площадь плоской фигуры, длина дуги кривой, объем тела вращения).
- •11. Понятие числового ряда и его суммы. Критерий Коши сходимости ряда. Необходимое условие сходимости.
- •12. Признаки Деламбера и Коши сходимости рядов с неотрицательными членами.
- •13. Интегральный признак Коши сходимости числового ряда.
- •14. Знакопеременные числовые ряды. Абсолютная и условная сходимость. Знакочередующиеся ряды. Признак Лейбница.
- •15. Функциональный ряд. Сумма ряда. Определение равномерной сходимости ряда. Критерий Коши равномерной сходимости функционального ряда.
- •16. Признак Вейерштрасса равномерной сходимости.
- •18. Степенной ряд. Теорема Абеля.
- •19. Радиус сходимости степенного ряда. Формула Коши-Адамара для радиуса сходимости степенного ряда.
- •21. Функции многих переменных. Понятие n-мерного евклидового пространства. Множество точек евклидового пространства. Последовательность точек и ее предел. Определение функции нескольких переменных.
- •22. Предел функции нескольких переменных. Непрерывность функции. Частные производные.
- •23. Определение дифференцируемой функции нескольких переменных и ее дифференциала. Производные и дифференциалы высших порядков.
- •24. Формула Тейлора для функции многих переменных. Экстремум функции нескольких переменных. Необходимое условие экстремума. Достаточное условие экстремума.
- •25. Двойной интеграл и его свойства. Сведение двойного интеграла к повторному.
- •27. Замена переменных в тройном интеграле. Цилиндрические и сферические координаты.
- •28. Вычисление площади гладкой поверхности, заданной параметрически и в явном виде.
- •29. Определение криволинейных интегралов первого и второго рода, их основные свойства и вычисление.
- •30. Формула Грина. Условия независимости криволинейного интеграла от пути интегрирования.
- •31. Поверхностные интегралы первого и второго рода, их основные свойства и вычисление.
- •32. Теорема Гаусса-Остроградского, ее запись в координатной и векторной (инвариантной) формах.
- •33. Формула Стокса, ее запись в координатной и векторной (инвариантной) формах.
- •34. Скалярное и векторное поля. Градиент, дивергенция, ротор. Потенциальное и соленоидальное поля.
- •35. Оператор Гамильтона. (набла) его применение (примеры).
- •36. Основные понятия, относящиеся к обыкновенным дифференциальным уравнениям (оду) первого порядка: общее и частное решения, общий интеграл, интегральная кривая. Задача Коши, ее геометрический смысл.
- •37. Интегрирование оду первого порядка с разделяющимися переменными и однородных.
- •38. Интегрирование линейных оду первого порядка и уравнения Бернулли.
- •39. Интегрирование оду первого порядка в полярных дифференциалах. Интегрирующий множитель.
- •40. Дифференциальные уравнения первого порядка, неразрешенные относительно производной. Метод введения параметра.
- •41. Уравнение n-го порядка с постоянными коэффициентами. Характеристическое уравнение. Фундаментальная система решений (фср) однородного уравнения, общее решение неоднородного уравнения.
- •42. Система линейных дифференциальных уравнений первого порядка. Фср однородной системы. Общее решение однородной системы.
25. Двойной интеграл и его свойства. Сведение двойного интеграла к повторному.
О пределение
двойного интеграла. Пусть на плоскости
XY задана функция
пределение
двойного интеграла. Пусть на плоскости
XY задана функция![]() и область (P) (область задания функции
f(x,y)), её площадь P. Произведём разбиение
площади сеткой кривых Pi, где Pi – частичная
область. Внутри частичной области
возьмём произвольную точку с координатами
(ξi,ηi). Составим интегральную сумму:
и область (P) (область задания функции
f(x,y)), её площадь P. Произведём разбиение
площади сеткой кривых Pi, где Pi – частичная
область. Внутри частичной области
возьмём произвольную точку с координатами
(ξi,ηi). Составим интегральную сумму:![]() .
Пусть λ – характеристика разбиения,
которая равна
.
Пусть λ – характеристика разбиения,
которая равна![]() ,
где di – диаметр частичной области.
Диаметр – максимальное расстояние
между любой парой точек в области.
Устремим λ к нулю. Если существует
предел интегральных сумм
,
где di – диаметр частичной области.
Диаметр – максимальное расстояние
между любой парой точек в области.
Устремим λ к нулю. Если существует
предел интегральных сумм![]() ,
то этот предел и называется двойным
интегралом:
,
то этот предел и называется двойным
интегралом:![]() .
.
Основные свойства двойного интеграла:
Свойство аддитивности:
![]()
Свойства линейности:
а) ![]()
б) ![]()
Модуль интеграла меньше или равен интегралу от модуля:
![]()
Теорема о среднем. Так как
![]()
то, проинтегрировав это неравенство, получим:
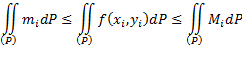
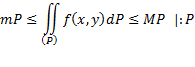
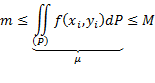
![]()
Где
![]()
Сведение двойного интеграла к повторному.
Т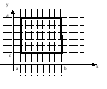 еорема.
Если функция f(x, y) интегрируема в
прямоугольнике, указанном на рисунке,
и если
еорема.
Если функция f(x, y) интегрируема в
прямоугольнике, указанном на рисунке,
и если ![]() и существует интеграл
и существует интеграл![]() ,
тогда существует повторный интеграл
,
тогда существует повторный интеграл![]() и
он равен двойному:
и
он равен двойному:![]() =
=![]() .
.
З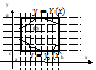 амечание.
Если f(x, y) интегрируема в прямоугольнике,
указанном на рисунке, и
амечание.
Если f(x, y) интегрируема в прямоугольнике,
указанном на рисунке, и ![]() и существует интеграл
и существует интеграл![]() тогда
существует повторный интеграл
тогда
существует повторный интеграл![]() .
.
Предположим, что
область D произвольного вида. Делаем
разбиение и проводим параллельные
линии. Заключим область (D) в прямоугольник
(D*), ![]() ,
и в нём определим функцию f*(x,y):
,
и в нём определим функцию f*(x,y):![]() .
.![]()
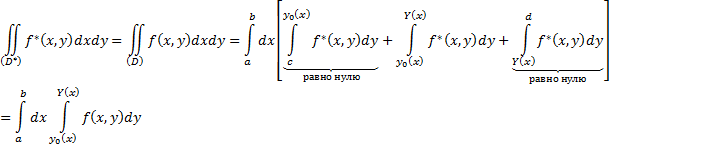
Формула в общем
виде: ![]() .
Так же доказывается, что
.
Так же доказывается, что![]()
Тройной интеграл, сведение его к повторному.
О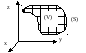 пределение
тройного интеграла. Пусть в некоторой
области (V) с границей (S) задана в каждой
точке функция f(x,y,z). Разобьём тело (V)
сеткой поверхностей на частичные области
(Vi). В каждой (Vi) возьмём произвольную
точку (ξi, ηi, ζi) и составим интегральную
сумму:
пределение
тройного интеграла. Пусть в некоторой
области (V) с границей (S) задана в каждой
точке функция f(x,y,z). Разобьём тело (V)
сеткой поверхностей на частичные области
(Vi). В каждой (Vi) возьмём произвольную
точку (ξi, ηi, ζi) и составим интегральную
сумму:![]() .
Устремим максимальный диаметр (макс.
расстояние между любой парой точек в
области) к нулю:
.
Устремим максимальный диаметр (макс.
расстояние между любой парой точек в
области) к нулю:![]() .
Тогда, если существует предел интегральных
сумм, то он равен тройному интегралу:
.
Тогда, если существует предел интегральных
сумм, то он равен тройному интегралу:![]() .
.
На всякий случай
определение интегральной суммы. Пусть
на нек-ом отрезке ![]() задана
задана![]() .
Произведём разбиение отрезка:
.
Произведём разбиение отрезка:![]() .
Число
.
Число![]() ,
называется интегральной суммой функции
f(x), соответствующей данному разбиению
T(ξi;xi) сегмента [a;b] и данному выбору
промежуточных точек ξi на частичных
сегментах [xi-1;xi], Δ –хар-тика разбиения:
,
называется интегральной суммой функции
f(x), соответствующей данному разбиению
T(ξi;xi) сегмента [a;b] и данному выбору
промежуточных точек ξi на частичных
сегментах [xi-1;xi], Δ –хар-тика разбиения:![]()
С ведение
к повторному интегралу. Рассмотрим
первый простейший случай. Пусть тело V
– прямоугольный параллелепипед. Проведём
секущую плоскость. Возьмём приращение
плоскости (жирные линии). Тогда:
ведение
к повторному интегралу. Рассмотрим
первый простейший случай. Пусть тело V
– прямоугольный параллелепипед. Проведём
секущую плоскость. Возьмём приращение
плоскости (жирные линии). Тогда:![]() .
.
Р ассмотрим
второй случай.
ассмотрим
второй случай.
Р ассмотрим
третий случай – область (V) цилиндрического
типа.
ассмотрим
третий случай – область (V) цилиндрического
типа.
![]()
26. Замена переменных в двойном интеграле. Пример: случай полярных координат.
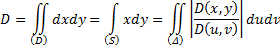
Вычислим интеграл
![]() ,
используя замену переменных
,
используя замену переменных![]() .
Рассмотрим интеграл как предел
интегральных сумм. Область (D) сеткой
кривых разделяется на частичные области
Di, внутри каждой частичной области берём
произвольные точки (xi, yi). Составляем
интегральную сумму:
.
Рассмотрим интеграл как предел
интегральных сумм. Область (D) сеткой
кривых разделяется на частичные области
Di, внутри каждой частичной области берём
произвольные точки (xi, yi). Составляем
интегральную сумму:![]() ,
где Di – площадь i-ой частичной области.
Устремим максимальный диаметр к нулю:
,
где Di – площадь i-ой частичной области.
Устремим максимальный диаметр к нулю:![]() .
По определению,
.
По определению,![]() .
Совершим замену переменных (*). При замене
(*) площадь
.
Совершим замену переменных (*). При замене
(*) площадь![]() .
.
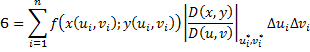
Если ![]() ,
то
,
то![]() и
и![]() ,
следовательно,
,
следовательно,![]()
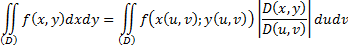
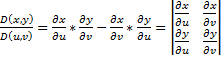 – якобиан преобразования (*).
– якобиан преобразования (*).
П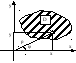 ример
с полярными координатами.
ример
с полярными координатами.![]()
![]()