
- •1. Определенный интеграл. Интегральная сумма. Верхняя и нижняя интегральные суммы. Их свойства.
- •2. Ограниченность интегрируемой функции.
- •Доказательство
- •3. Критерий интегрируемости ограниченной на отрезке функции.
- •4. Теорема об интегрируемости монотонной на отрезке, а также непрерывной на отрезке функций.
- •5. Основные свойства определенного интеграла.
- •6. Формула среднего значения для определенного интеграла.
- •7. Интеграл с переменным верхним пределом. Его непрерывность и дифференцируемость.
- •8. Формула Ньютона-Лейбница для определенного интеграла.
- •9. Вычисление определенного интеграла по частям и заменой переменной.
- •10. Применение определенного интеграла (площадь плоской фигуры, длина дуги кривой, объем тела вращения).
- •11. Понятие числового ряда и его суммы. Критерий Коши сходимости ряда. Необходимое условие сходимости.
- •12. Признаки Деламбера и Коши сходимости рядов с неотрицательными членами.
- •13. Интегральный признак Коши сходимости числового ряда.
- •14. Знакопеременные числовые ряды. Абсолютная и условная сходимость. Знакочередующиеся ряды. Признак Лейбница.
- •15. Функциональный ряд. Сумма ряда. Определение равномерной сходимости ряда. Критерий Коши равномерной сходимости функционального ряда.
- •16. Признак Вейерштрасса равномерной сходимости.
- •18. Степенной ряд. Теорема Абеля.
- •19. Радиус сходимости степенного ряда. Формула Коши-Адамара для радиуса сходимости степенного ряда.
- •21. Функции многих переменных. Понятие n-мерного евклидового пространства. Множество точек евклидового пространства. Последовательность точек и ее предел. Определение функции нескольких переменных.
- •22. Предел функции нескольких переменных. Непрерывность функции. Частные производные.
- •23. Определение дифференцируемой функции нескольких переменных и ее дифференциала. Производные и дифференциалы высших порядков.
- •24. Формула Тейлора для функции многих переменных. Экстремум функции нескольких переменных. Необходимое условие экстремума. Достаточное условие экстремума.
- •25. Двойной интеграл и его свойства. Сведение двойного интеграла к повторному.
- •27. Замена переменных в тройном интеграле. Цилиндрические и сферические координаты.
- •28. Вычисление площади гладкой поверхности, заданной параметрически и в явном виде.
- •29. Определение криволинейных интегралов первого и второго рода, их основные свойства и вычисление.
- •30. Формула Грина. Условия независимости криволинейного интеграла от пути интегрирования.
- •31. Поверхностные интегралы первого и второго рода, их основные свойства и вычисление.
- •32. Теорема Гаусса-Остроградского, ее запись в координатной и векторной (инвариантной) формах.
- •33. Формула Стокса, ее запись в координатной и векторной (инвариантной) формах.
- •34. Скалярное и векторное поля. Градиент, дивергенция, ротор. Потенциальное и соленоидальное поля.
- •35. Оператор Гамильтона. (набла) его применение (примеры).
- •36. Основные понятия, относящиеся к обыкновенным дифференциальным уравнениям (оду) первого порядка: общее и частное решения, общий интеграл, интегральная кривая. Задача Коши, ее геометрический смысл.
- •37. Интегрирование оду первого порядка с разделяющимися переменными и однородных.
- •38. Интегрирование линейных оду первого порядка и уравнения Бернулли.
- •39. Интегрирование оду первого порядка в полярных дифференциалах. Интегрирующий множитель.
- •40. Дифференциальные уравнения первого порядка, неразрешенные относительно производной. Метод введения параметра.
- •41. Уравнение n-го порядка с постоянными коэффициентами. Характеристическое уравнение. Фундаментальная система решений (фср) однородного уравнения, общее решение неоднородного уравнения.
- •42. Система линейных дифференциальных уравнений первого порядка. Фср однородной системы. Общее решение однородной системы.
32. Теорема Гаусса-Остроградского, ее запись в координатной и векторной (инвариантной) формах.
В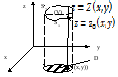 координатной форме.
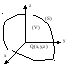
Рассмотрим тело (V)
в пространстве с ограничивающей
поверхностью (S).
координатной форме.
Рассмотрим тело (V)
в пространстве с ограничивающей
поверхностью (S).
Рассмотрим некую
функцию R(x,y,z),
заданную в области (V)
и на границе, непрерывную в этой области
и на границе вместе со своими частными
производными первого порядка. Рассмотрим
интеграл ![]() .
Спроецируем тело на область D.
Возьмём точку (x,y).
.
Спроецируем тело на область D.
Возьмём точку (x,y).
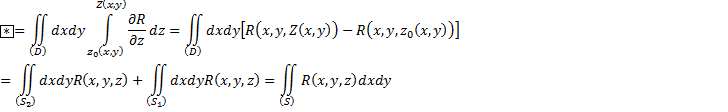
С делаем
то же самое, но с проекцией на осиy
и z.
делаем
то же самое, но с проекцией на осиy
и z.
Теперь спроектируем на оси x и z.
![]()
Складывая эти
формулы, получаем формулу
Остроградского-Гаусса:
![]() .
Формула сводит интеграл от объёма к
интегралу по границе.
.
Формула сводит интеграл от объёма к
интегралу по границе.
Если ![]() и
и ![]() или
или ![]() и
и ![]() или
или ![]() и
и ![]() ,
тогда
,
тогда ![]() .
А если
.
А если ![]() ,
,
![]() и
и ![]() ,
то:
,
то: ![]() .
.
В
общем виде теорема звучит так.
Пусть в замкнутой ограниченной области
(V)
заданы функции P(x,y,z),
Q(x,y,z)
и R(x,y,z),
непрерывные на (V)
вместе со своими частными производными
первого порядка. Тогда имеет место
следующее тождество: ![]() .
.
З апись
формулы в векторном виде.
Пусть
апись
формулы в векторном виде.
Пусть ![]() .
В обычном виде формула выглядит так:
.
В обычном виде формула выглядит так:
![]()
Левую часть можно
записать так: ![]() ,
,
![]() ,
,
![]() .
Следовательно:
.
Следовательно: ![]() ,
так как
,
так как ![]() .
Мы получили поток
вектора через замкнутую поверхность.
Правую часть можно записать как
дивергенцию
(расходимость):
.
Мы получили поток
вектора через замкнутую поверхность.
Правую часть можно записать как
дивергенцию
(расходимость):
![]() .
В итоге формула
Гаусса-Остроградского в векторном виде:
.
В итоге формула
Гаусса-Остроградского в векторном виде:
![]() .
Читается так: поток вектора через
замкнутую поверхность равен интегралу
по объёму от его дивергенции.
.
Читается так: поток вектора через
замкнутую поверхность равен интегралу
по объёму от его дивергенции.
Дивергенцией
векторного поля A
в точке MÎV
называется производная функции ![]() по объему в этой точке:
по объему в этой точке: ![]() .
.
33. Формула Стокса, ее запись в координатной и векторной (инвариантной) формах.
![]() .
.![]() {ф. Грина}=
{ф. Грина}=
=
![]() .
Аналогично
.
Аналогично![]() c
c![]() ,
,![]() c
c![]() .
.
Теорема: Пусть в некоторой окрестности поверхности S функции Р(х, у, z), Q(x, у, z) и R(x, у, z) непрерывны и имеют непрерывные частные, производные первого порядка. Тогда имеет место следующее соотношение:
![]() .
(Формула Стокса).
.
(Формула Стокса).
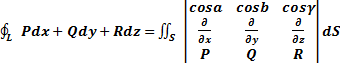 .
.
Инвариантная запись
формулы Стокса: Используя выражение
для ![]() в ортогональном базисе
в ортогональном базисе![]() ,
,![]() :
:
![]() .
Укажем на поверхности S определенную
сторону, т.е. укажем непрерывное поле
единичных нормалей
.
Укажем на поверхности S определенную
сторону, т.е. укажем непрерывное поле
единичных нормалей![]() .
Используя стандартное обозначение
cosx, cosy, cos
.
Используя стандартное обозначение
cosx, cosy, cos![]() для координат единичного вектора
нормали
для координат единичного вектора
нормали![]() к поверхности S получим:
к поверхности S получим:![]() .
Из соотношения видно, левая часть формулы
Стокса может быть записана в виде
.
Из соотношения видно, левая часть формулы
Стокса может быть записана в виде![]() .
Скалярное произведение:
.
Скалярное произведение:![]() и элемент площади
и элемент площади![]() поверхности S не зависят от выбора
декартовой прямоугольной системы
координат в пространстве, и при переходе
к новому ортогональному базису
поверхности S не зависят от выбора
декартовой прямоугольной системы
координат в пространстве, и при переходе
к новому ортогональному базису![]() ',
',![]() левая часть формулы не изменит своего
значения и формы – инвариантна.
левая часть формулы не изменит своего
значения и формы – инвариантна.
Рассмотрим ![]() .
Пусть
.
Пусть![]() – единичный вектор касательной в точках
границы L поверхности S, cosa, cosb, cos
– единичный вектор касательной в точках
границы L поверхности S, cosa, cosb, cos![]() – координаты этого вектора.
– координаты этого вектора.![]() ,
,![]() .
Т.о
.
Т.о![]() – циркуляция векторного поля p по кривой
L.
– циркуляция векторного поля p по кривой
L.![]() -
инвариант. Получаем
-
инвариант. Получаем![]() =
=![]() .
.
34. Скалярное и векторное поля. Градиент, дивергенция, ротор. Потенциальное и соленоидальное поля.
Скалярное поле. Градиент скалярного поля и его свойства. Вычисление градиента в декартовых координатах.
Пусть D – область на плоскости или в пространстве. Говорят, что в D задано скалярное поле, если каждой точке области D ставится в соответствие некая функция U(M).
Определение
по-другому. Скалярное поле определяется
скалярной функцией точки ![]() ,
где M(x,y,z) – точка пространства,
,
где M(x,y,z) – точка пространства,![]() – её радиус-вектор.
– её радиус-вектор.
Определение
градиента. Градиентом скалярной функции
u(M), определенной и дифф в некоторой
области D, называется вектор ![]() .
.![]() .
Знак
.
Знак![]() - это вектор Набла.
- это вектор Набла.![]()
![]() (
(![]() – единичный вектор с координатами:
– единичный вектор с координатами:![]() ).
).
Из последнего
выражения видно, что ![]() максимально, когда
максимально, когда![]() совпадает с направлением градиента.
Следовательно, градиент показывает
направление наибольшего изменения
скорости функции.
совпадает с направлением градиента.
Следовательно, градиент показывает
направление наибольшего изменения
скорости функции.
Градиент скалярного поля – вектор.
Свойства градиента:
![]()
![]()
![]()
![]()
![]()
![]()
![]()
Векторное поле.
Если каждой точке М некоторой области
V пространства соответствует значение
некоторой векторной величины ![]() (M),
то говорят, что в области V задано
векторное поле
(M),
то говорят, что в области V задано
векторное поле![]() (M). Примеры векторных полей – поле
тяготения, поля электрической и магнитной
напряжённостей, поле скоростей частиц
движущейся жидкости.
(M). Примеры векторных полей – поле
тяготения, поля электрической и магнитной
напряжённостей, поле скоростей частиц
движущейся жидкости.
Если в некоторой
декартовой системе координат вектор
![]() (M) имеет координаты Р(M), Q(M), R(M), то
(M) имеет координаты Р(M), Q(M), R(M), то![]() .
Таким образом, задание векторного поля
.
Таким образом, задание векторного поля![]() (M)
эквивалентно заданию трёх скалярных
полей Р(M), Q(M), R(M). Будем называть векторное
поле гладким, если его координатные
функции - гладкие скалярные поля.
(M)
эквивалентно заданию трёх скалярных
полей Р(M), Q(M), R(M). Будем называть векторное
поле гладким, если его координатные
функции - гладкие скалярные поля.
Градиентом
дифференцируемого скалярного поля
u(M)=u(x,y,z) называется вектор ![]() .
Т.е. сумма частных производных умноженных
на соответствующие единичные вектора.
.
Т.е. сумма частных производных умноженных
на соответствующие единичные вектора.
В общем случае градиент вводится как векторная характеристика скалярного поля — то есть области, каждой точке которой соответствует значение определенного скаляра. Градиент характеризует, насколько быстро меняется скалярная величина в том или ином месте этого поля.
Потенциальные
векторные поля. Векторное поле A =
{Ax, Ay, Az} называется потенциальным, если
вектор А является градиентом некоторой
скалярной функции u = u(x, y, z): A = grad u
= ![]() (16.7).
(16.7).
При этом функция u называется потенциалом данного векторного поля.
Выясним, при каких
условиях векторное поле является
потенциальным. Так как из (16.7) следует,
что ![]() ,
То
,
То![]() ,
,![]() =
=![]() ,
,![]() =
=![]() .
так как смешанная производная второго
порядка не зависит от порядка
дифференцирования. Из этих равенств
легко получаем, что rot A = 0 -условие
потенциальности векторного поля.
.
так как смешанная производная второго
порядка не зависит от порядка
дифференцирования. Из этих равенств
легко получаем, что rot A = 0 -условие
потенциальности векторного поля.
Ротором векторного
поля ![]() (M)
в точке
(M)
в точке![]() называется векторная величина (векторное
поле):
называется векторная величина (векторное
поле):![]() .
Если выразить
.
Если выразить![]() через оператор Гамильтона набла:
через оператор Гамильтона набла:![]() равен векторному произведению
равен векторному произведению![]() .
Действительно,
.
Действительно,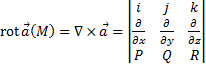 .
.
Пусть в некоторой
области D задано непрерывное векторное
поле ![]() (M)=
(M)=![]() (x,y,z). Потоком векторного поля
(x,y,z). Потоком векторного поля![]() через ориентированную кусочно-гладкую
поверхность S, расположенную в области
D, называется интеграл
через ориентированную кусочно-гладкую
поверхность S, расположенную в области
D, называется интеграл![]() ,
где
,
где![]() – единичный вектор нормали к поверхности
S, указывающий на ее ориентацию, а
– единичный вектор нормали к поверхности
S, указывающий на ее ориентацию, а![]() – элемент площади поверхности S.
– элемент площади поверхности S.
Векторное поле ![]() называется соленоидальным в области
D, если поток этого поля через любую
кусочно-гладкую несамопересекающуюся
поверхность, расположенную в D и
представляющую собой границу некоторой
ограниченной подобласти области D, равен
нулю.
называется соленоидальным в области
D, если поток этого поля через любую
кусочно-гладкую несамопересекающуюся
поверхность, расположенную в D и
представляющую собой границу некоторой
ограниченной подобласти области D, равен
нулю.
Е сли
дивергенция равна нулю, то есть
сли
дивергенция равна нулю, то есть![]() ,
то поле вектора
,
то поле вектора![]() называется соленоидальным.
называется соленоидальным.

![]() ,
поэтому поток везде, на каждом сечении
трубки, одинаков.
,
поэтому поток везде, на каждом сечении
трубки, одинаков.
Для того чтобы
непрерывно дифференцируемое векторное
поле ![]() было соленоидальным в объемно-односвязной
области D, необходимо и достаточно, чтобы
во всех точках D выполнялось равенство
было соленоидальным в объемно-односвязной
области D, необходимо и достаточно, чтобы
во всех точках D выполнялось равенство![]() .
Где дивергенцией (“расходимость”)
векторного поля
.
Где дивергенцией (“расходимость”)
векторного поля![]() называется скалярная функция
называется скалярная функция![]()
Циркуляцией
векторного поля называется криволинейный
интеграл второго рода, взятый по
произвольному замкнутому контуру L: ![]()
Г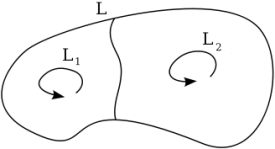 де
де![]() — векторное поле (или вектор-функция),
определенное в некоторой области D,
содержащей в себе контур L,
— векторное поле (или вектор-функция),
определенное в некоторой области D,
содержащей в себе контур L,![]() — бесконечно малое приращение
радиус-вектора
— бесконечно малое приращение
радиус-вектора![]() вдоль контура. Окружность на символе
интеграла подчёркивает тот факт, что
интегрирование производится по замкнутому
контуру.
вдоль контура. Окружность на символе
интеграла подчёркивает тот факт, что
интегрирование производится по замкнутому
контуру.
Циркуляция по
контуру, ограничивающему несколько
смежных поверхностей, равна сумме
циркуляций по контурам, ограничивающим
каждую поверхность в отдельности, то
есть ![]()
![]() – формула Стокса в векторном виде.
– формула Стокса в векторном виде.
Вихревым вектором
(вихрем) или ротором векторного поля
![]() называется вектор, имеющий координаты:
называется вектор, имеющий координаты: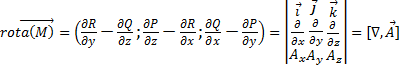
Ротор в декартовых
координатах: ![]()
Если ![]() ,
то векторное поле
,
то векторное поле![]() называется безвихревым или потенциальном.
называется безвихревым или потенциальном.
