6. Формула среднего значения для определенного интеграла.

Теорема о среднем. Если f(x) непрерывна на отрезке [a,b], то существует точка , такая что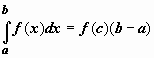. Док-во. Функция, непрерывная на отрезке, принимает на этом отрезке своё наименьшее m и наибольшее M значения. Тогда. Число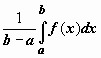заключено между минимальным и максимальным значениями функции на отрезке. Одно из свойств функции, непрерывной на отрезке, заключается в том, что эта функция принимает любое значение, расположенное между m и M. Таким образом, существует точка, такая что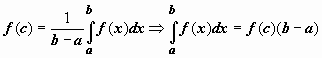. 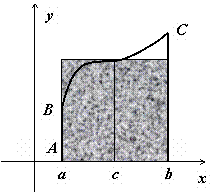Это свойство имеет простую геометрическую интерпретацию: еслинепрерывна на отрезке [a,b], то существует точкатакая, что площадь криволинейной трапеции ABCD равна площади прямоугольника с основанием [a,b] и высотой f(c) (на рисунке выделен цветом).

7. Интеграл с переменным верхним пределом. Его непрерывность и дифференцируемость.

Рассмотрим функцию f (x), интегрируемую по Риману на отрезке [a, b]. Раз она интегрируема на [a, b], то она также интегрируема на [a, x] ∀x ∈ [a, b]. Тогда при каждом x ∈ [a, b] имеет смысл выражение , и при каждом x оно равно некоторому числу.

Таким образом, каждому x ∈ [a, b] поставлено в соответствие некоторое число ,

т.е. на [a, b] задана функция:

(3.1)

Определение:

Функция F (x), заданная в (3.1), а также само выражение называется

интегралом с переменным верхним пределом. Она определена на всем отрезке [a, b]

интегрируемости функции f (x).

Теорема:

Условие: f (t) непрерывна на [a, b], а функция F (x) задана формулой (3.1).

Утверждение: Функция F(x) дифференцируема на [a, b], причем F (x) = f (x).

(В точке a она дифференцируема справа, а в точке b – слева.)

Доказательство:

Поскольку для функции одной переменной F (x) дифференцируемость равносильна существованию производной во всех точках (в точке a справа, а в точке b – слева), то мы найдем производную F (x). Рассмотрим разность

Таким образом,

,

при этом точка ξ лежит на отрезке [x, x + ∆x] (или [x + ∆x, x] если ∆x < 0).

Теперь вспомним, что производная функции F(x) в заданной точке x ∈ [a, b] равна пределу разностного отношения: . Из равенства имеем:

,

Устремляя теперь ∆x → 0, в левой части данного равенства получим F’(x), a в правой

Вспомним определение непрерывности функции f (t) в точке x:

Пусть x1 в этом определении равен ξ. Поскольку ξ ∈ [x + ∆x, x] (ξ ∈ [x, x + ∆x]), а

∆x → 0, то |x − ξ| → 0, и по определению непрерывности, f (ξ) → f (x). Отсюда имеем:

F’(x) = f (x).

Следствие:

Условие: f (x) непрерывна на [a, b].

Утверждение: Любая первообразная функции f (x) имеет вид

где C ∈ R – некоторая константа.

Доказательство. По теореме 3.1 функция является первообразной для f(x). Предположим, что G(x) – другая первообразная f (x). Тогда G’(x) = f(x) и для функции F(x) − G(x) имеем: (F (x) + G(x))’ = F’(x)−G’(x) = f (x)−f(x) ≡ 0. Значит, производная функции F (x)−G(x)

равна нулю, следовательно, эта функция есть постоянная: F(x) − G(x) = const.