11. Понятие числового ряда и его суммы. Критерий Коши сходимости ряда. Необходимое условие сходимости.

Выражение(1)

где (uk)kÎN — заданная числовая последовательность, называется числовым рядом. Конечные суммы S1 = u1, S2 = u1 + u2, .... Sn = u1 + u2 +...+ un, называются частичными суммами ряда (1).

Если существует конечный предел последовательности частичных сумм (2)

то ряд (1) называется сходящимся, а число S—суммой ряда (1)

Необходимое условие сходимости:

Если ряд (1) сходится, то

Доказательство:

Пусть ряд u1+u2+…+un… сходится, то есть существует конечный предел =S. Тогда имеет место также равенство=S, так как при nи (n-1). Вычитая почленно из первого равенства второе, получаем-==un=0, что и требовалось доказать.

Критерий Коши:

Для того чтобы числовой ряд (1) был сходящимся, необходимо и достаточно, чтобы для любого ε > 0 су­ществовало N = N(ε) такое, что для всех n > N и р = 1, 2, … выполнялось неравенство:

Доказательство:

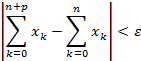
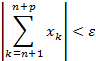
Частный случай:

При :, следовательно,(необходимое условие сходимости ряда).

12. Признаки Деламбера и Коши сходимости рядов с неотрицательными членами.

Признак Даламбера:

Пусть дан знакоположительный числовой ряд

(7)

и пусть существует предел При p<1 ряд (7) сходится, при p>1 ряд (7) расходится.

Доказательство:

По условию существует предел . Это означает, что для любого положительного числа Е существует такой номер N, что для всех номеров n³N выполняется условие

или p-E<(10)

Пусть сначала p<1. Выберем Е так, что p+E=q<1. Для всех n³N имеем … или

или

(11)

Рассмотрим ряды:

(12)

. (13)

Ряд (13) сходится, так как он является бесконечно убывающей геометрической прогрессией. Тогда ряд (12) сходится, учитывая (11), по признаку сравнения. Ряд (7) сходится по теореме 1.

Пусть теперь p>1. Выберем Е так, что p-E>1. Тогда из левой части неравенства (10) следует, что при n³N выполняется или un+1>un, то есть члены ряда возрастают с возрастанием номера n. Поэтомуun¹0, следовательно, ряд расходится по следствию из необходимого признака сходимости. Теорема доказана.

 

Замечания:

1. Если расходимость ряда установлена с помощью признака Даламбера, то un¹0.

2. При р=1 признак Даламбера не даёт ответа о сходимости ряда. В этом случае нужно применять другие признаки сходимости.

3. Признак Даламбера рекомендуется применять при наличии в выражении общего члена ряда показательной функции или факториала.

Признак Коши:

Пусть дан знакоположительный числовой ряд u1+u2+…+un… (7)

и пусть существует предел При p<1 ряд (7) сходится, при p>1 ряд (7) расходится.

Доказательство:

По условию существует Это означает, что для любого положительного числа Е существует такой номер N, что для всех n³N выполняется условие || <E или

p-E<<p+E. (14)

Пусть p<1. Выберем Е таким, чтобы выполнялось p+E=q<1. Тогда из (14) получаем <q или un<qn для всех n³N. Рассмотрим ряды

(15)

(16)

Ряд (16) сходится, так как он является бесконечно убывающей геометрической прогрессией. Ряд (15) сходится, учитывая, что un<qn для всех n³N, по признаку сравнения, следовательно, по теореме 1 сходится ряд (7).

Пусть теперь p>1. Выберем Е так, чтобы выполнялось условие p-E >1. Тогда из (14) получаем >1 или un>1, следовательно,un¹0 и ряд (7) расходится по следствию из необходимого признака сходимости. Теорема доказана.