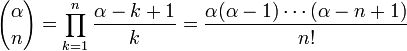- •1. Определенный интеграл. Интегральная сумма. Верхняя и нижняя интегральные суммы. Их свойства.
- •2. Ограниченность интегрируемой функции.
- •Доказательство
- •3. Критерий интегрируемости ограниченной на отрезке функции.
- •4. Теорема об интегрируемости монотонной на отрезке, а также непрерывной на отрезке функций.
- •5. Основные свойства определенного интеграла.
- •6. Формула среднего значения для определенного интеграла.
- •7. Интеграл с переменным верхним пределом. Его непрерывность и дифференцируемость.
- •8. Формула Ньютона-Лейбница для определенного интеграла.
- •9. Вычисление определенного интеграла по частям и заменой переменной.
- •10. Применение определенного интеграла (площадь плоской фигуры, длина дуги кривой, объем тела вращения).
- •11. Понятие числового ряда и его суммы. Критерий Коши сходимости ряда. Необходимое условие сходимости.
- •12. Признаки Деламбера и Коши сходимости рядов с неотрицательными членами.
- •13. Интегральный признак Коши сходимости числового ряда.
- •14. Знакопеременные числовые ряды. Абсолютная и условная сходимость. Знакочередующиеся ряды. Признак Лейбница.
- •15. Функциональный ряд. Сумма ряда. Определение равномерной сходимости ряда. Критерий Коши равномерной сходимости функционального ряда.
- •16. Признак Вейерштрасса равномерной сходимости.
- •18. Степенной ряд. Теорема Абеля.
- •19. Радиус сходимости степенного ряда. Формула Коши-Адамара для радиуса сходимости степенного ряда.
- •21. Функции многих переменных. Понятие n-мерного евклидового пространства. Множество точек евклидового пространства. Последовательность точек и ее предел. Определение функции нескольких переменных.
- •22. Предел функции нескольких переменных. Непрерывность функции. Частные производные.
- •23. Определение дифференцируемой функции нескольких переменных и ее дифференциала. Производные и дифференциалы высших порядков.
- •24. Формула Тейлора для функции многих переменных. Экстремум функции нескольких переменных. Необходимое условие экстремума. Достаточное условие экстремума.
- •25. Двойной интеграл и его свойства. Сведение двойного интеграла к повторному.
- •27. Замена переменных в тройном интеграле. Цилиндрические и сферические координаты.
- •28. Вычисление площади гладкой поверхности, заданной параметрически и в явном виде.
- •29. Определение криволинейных интегралов первого и второго рода, их основные свойства и вычисление.
- •30. Формула Грина. Условия независимости криволинейного интеграла от пути интегрирования.
- •31. Поверхностные интегралы первого и второго рода, их основные свойства и вычисление.
- •32. Теорема Гаусса-Остроградского, ее запись в координатной и векторной (инвариантной) формах.
- •33. Формула Стокса, ее запись в координатной и векторной (инвариантной) формах.
- •34. Скалярное и векторное поля. Градиент, дивергенция, ротор. Потенциальное и соленоидальное поля.
- •35. Оператор Гамильтона. (набла) его применение (примеры).
- •36. Основные понятия, относящиеся к обыкновенным дифференциальным уравнениям (оду) первого порядка: общее и частное решения, общий интеграл, интегральная кривая. Задача Коши, ее геометрический смысл.
- •37. Интегрирование оду первого порядка с разделяющимися переменными и однородных.
- •38. Интегрирование линейных оду первого порядка и уравнения Бернулли.
- •39. Интегрирование оду первого порядка в полярных дифференциалах. Интегрирующий множитель.
- •40. Дифференциальные уравнения первого порядка, неразрешенные относительно производной. Метод введения параметра.
- •41. Уравнение n-го порядка с постоянными коэффициентами. Характеристическое уравнение. Фундаментальная система решений (фср) однородного уравнения, общее решение неоднородного уравнения.
- •42. Система линейных дифференциальных уравнений первого порядка. Фср однородной системы. Общее решение однородной системы.
18. Степенной ряд. Теорема Абеля.
Важным случаем функциональных рядов являются степенные ряды:
![]() (13)
(13)
или
![]()
Для выяснения
свойств степенных рядов достаточно
ограничиться рассмотрением рядов вида
(13), так как ряд по степеням
![]() легко свести к виду (13) заменой переменных
легко свести к виду (13) заменой переменных![]() ,
т.е. переносом начала координат в точку
,
т.е. переносом начала координат в точку![]()
Для выяснения характера области сходимости степенного ряда сформулируем следующую теорему:
Теорема 6.1. (Абеля):
Пусть степенной
ряд (13) сходится в точке
![]() Тогда он сходится абсолютно в любой
точке х, для которой
Тогда он сходится абсолютно в любой
точке х, для которой![]() и равномерно в любой области
и равномерно в любой области![]() .
.
Если степенной ряд
(13) расходится в точке
![]() то он расходится и во всех точках
то он расходится и во всех точках![]() таких, что
таких, что![]() .
.
Для определения области сходимости степенного ряда используется либо признак Даламбера, либо признак Коши.
Рассмотрим степенной ряд:
![]() .
(14)
.
(14)
Вычислим предел:
 .(15)
.(15)
Если существует
предел (15), то ряд (14) сходится, если
![]() ,
и расходится, если
,
и расходится, если![]() .
Следовательно, ряд (14) сходится
абсолютно, если
.
Следовательно, ряд (14) сходится
абсолютно, если
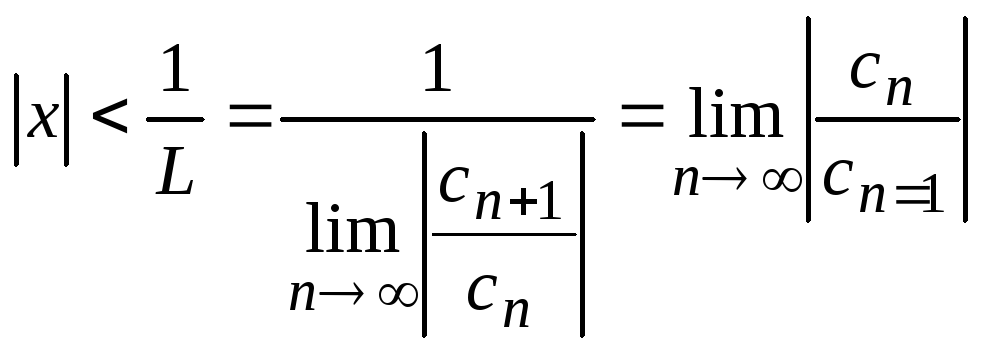 ,
,
и расходится, если
![]() .
.
Определение:
Число
![]() ,
такое, что для всех x, удовлетворяющих
условию
,
такое, что для всех x, удовлетворяющих
условию![]() ряд (13) сходится, а для всех х
удовлетворяющих условию
ряд (13) сходится, а для всех х
удовлетворяющих условию![]() ряд расходится, называется радиусом
сходимости ряда.
ряд расходится, называется радиусом
сходимости ряда.
Формула для радиуса сходимости, получаемая с помощью признака Даламбера, имеет вид
![]() (16)
(16)
Область сходимости ряда - так называют множество точек сходимости функционального ряда, т.е. множество значений аргумента х, для которых ряд (бесконечная сумма) сходится
Пример 6.1.
Найти область сходимости ряда Область сходимости ряда
![]() при
при
![]() .
.
По признаку Даламбера:

что означает, что ряд сходится на всей оси Х.
19. Радиус сходимости степенного ряда. Формула Коши-Адамара для радиуса сходимости степенного ряда.
1) Степенной ряд
сходится абсолютно на некотором интервале
![]() .
Иными словами, если мы выбираем любое
значение «икс» из интервала
.
Иными словами, если мы выбираем любое
значение «икс» из интервала![]() и
подставляем его в общий член степенного
ряда, то у нас получается абсолютно
сходящийся числовой ряд. Такой интервал
и
подставляем его в общий член степенного
ряда, то у нас получается абсолютно
сходящийся числовой ряд. Такой интервал![]() и
называется интервалом сходимости
степенного ряда.
и
называется интервалом сходимости
степенного ряда.
Радиус сходимости,
если совсем просто, это половина длины
интервала сходимости:
![]()
2) Степенной ряд
сходится абсолютно при любом значении
![]() .
То есть, какое бы значение «икс» мы не
подставили в общий член степенного ряда
– в любом случае у нас получится абсолютно
сходящийся числовой ряд. Интервал
сходимости и область сходимости в данном
случае совпадают:
.
То есть, какое бы значение «икс» мы не
подставили в общий член степенного ряда
– в любом случае у нас получится абсолютно
сходящийся числовой ряд. Интервал
сходимости и область сходимости в данном
случае совпадают:![]() .
Радиус сходимости:
.
Радиус сходимости:![]() .
Рисунок приводить не буду, думаю, нет
необходимости.
.
Рисунок приводить не буду, думаю, нет
необходимости.
3) Степенной ряд
сходится в единственной точке. Если ряд
имеет вид
![]() ,
то он будет сходиться в единственной
точке
,
то он будет сходиться в единственной
точке![]() .
В этом случае интервал сходимости и
область сходимости ряда тоже совпадают
и равны единственному числу – нулю:
.
В этом случае интервал сходимости и
область сходимости ряда тоже совпадают
и равны единственному числу – нулю:![]() .
Если ряд имеет вид
.
Если ряд имеет вид![]() ,
то он будет сходиться в единственной
точке
,
то он будет сходиться в единственной
точке![]() ,
если ряд имеет вид
,
если ряд имеет вид![]() ,
то, понятно, – в точке «минус а». Радиус
сходимости ряда во всех случаях,
естественно, нулевой:
,
то, понятно, – в точке «минус а». Радиус
сходимости ряда во всех случаях,
естественно, нулевой:![]()
Радиус сходимости степенного ряда определяется по формуле Коши-Адамара

Здесь
![]() —
верхний предел последовательности
—
верхний предел последовательности![]() .
Он всегда существует (конечный или
бесконечный), и притом единственный. В
случае
.
Он всегда существует (конечный или
бесконечный), и притом единственный. В
случае![]() полагают
полагают![]() ,
а в случае
,
а в случае![]() полагают
полагают![]() .
.
20. Ряд Тейлора. Теорема Тейлора о разложимости функции в ряд Тейлора. Разложение основных элементарных функций в ряд Тейлора-Маклорена: ex, sinx, cosx, (1+x)a, ln(1+x).
Пусть функция
![]() бесконечно
дифференцируема в некоторой окрестности
точки
бесконечно
дифференцируема в некоторой окрестности
точки![]() .
Формальный ряд
.
Формальный ряд
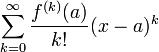
называется рядом
Тейлора функции
![]() в
точке
в
точке![]() .
.
В случае, если
![]() ,
этот ряд также называется рядом Маклорена.
,
этот ряд также называется рядом Маклорена.
Пусть ![]() .
Тогда ряд
.
Тогда ряд![]() называется
рядом Тейлора функции
называется
рядом Тейлора функции![]() в
точке
в
точке![]() .
.
Если ![]() ,
то
,
то![]() по
формуле Тейлора:
по
формуле Тейлора:![]()
, где ![]() -
остаточный член формулы Тейлора, т.е.
-
остаточный член формулы Тейлора, т.е.![]() ,
где
,
где![]() -
n-ая частичная сумма ряда Тейлора
функции
-
n-ая частичная сумма ряда Тейлора
функции![]() в
точке
в
точке![]() .
.![]() ряд
Тейлора сходится на
ряд
Тейлора сходится на![]() тогда
и только тогда, когда
тогда
и только тогда, когда![]()
![]()
Пусть ![]() и
и![]()
![]()
![]()
![]() ,
тогда на
,
тогда на![]()
![]()
Доказательство:
![]() ,
где
,
где ![]() -
остаточный член формулы Тейлора в форме
Лагранжа:
-
остаточный член формулы Тейлора в форме
Лагранжа:
![]()
![]()
![]()
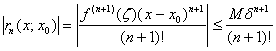 .
.
Рассмотрим
ряд ![]() ,
,![]() по
признаку Даламбера ряд сходится
по
признаку Даламбера ряд сходится![]() .
Перейдем к пределу при
.
Перейдем к пределу при![]() в
неравенстве
в
неравенстве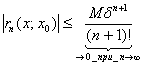
![]()
![]()
![]()
![]() на
на![]() .
.
Теорема Тейлора
Пусть функция f(x) имеет в точке х = а и некоторой ее окрестности производные порядка до (n+1) включительно.{ Т.е. и все предыдущие до порядка n функции и их производные непрерывны и дифференцируемы в этой окрестности}.
2) Пусть х- любое
значение из этой окрестности, но а
х
Тогда между точками х и а найдется
такая точка ,
что справедлива формула:
![]() это
выражение называется формулой Тейлора,
а выражение:
это
выражение называется формулой Тейлора,
а выражение:![]() называется
остаточным членом в форме
Лагранжа.
Доказательство. Представим
функцию f(x) в виде некоторого многочлена
Pn(x), значение которого в точке х = а равно
значению функции f(x), а значения его
производных равно значениям соответствующих
производных функции в точке х =
а.
называется
остаточным членом в форме
Лагранжа.
Доказательство. Представим
функцию f(x) в виде некоторого многочлена
Pn(x), значение которого в точке х = а равно
значению функции f(x), а значения его
производных равно значениям соответствующих
производных функции в точке х =
а.![]() (1)
Многочлен
Pn(x) будет близок к функции f(x). Чем больше
значение n, тем ближе значения многочлена
к значениям функции, тем точнее он
повторяет функцию.
Представим этот
многочлен с неопределенными пока
коэффициентами:
(1)
Многочлен
Pn(x) будет близок к функции f(x). Чем больше
значение n, тем ближе значения многочлена
к значениям функции, тем точнее он
повторяет функцию.
Представим этот
многочлен с неопределенными пока
коэффициентами:![]() (2)
Для
нахождения неопределенных коэффициентов
вычисляем производные многочлена в
точке х = а и составляем систему
уравнений:
(2)
Для
нахождения неопределенных коэффициентов
вычисляем производные многочлена в
точке х = а и составляем систему
уравнений: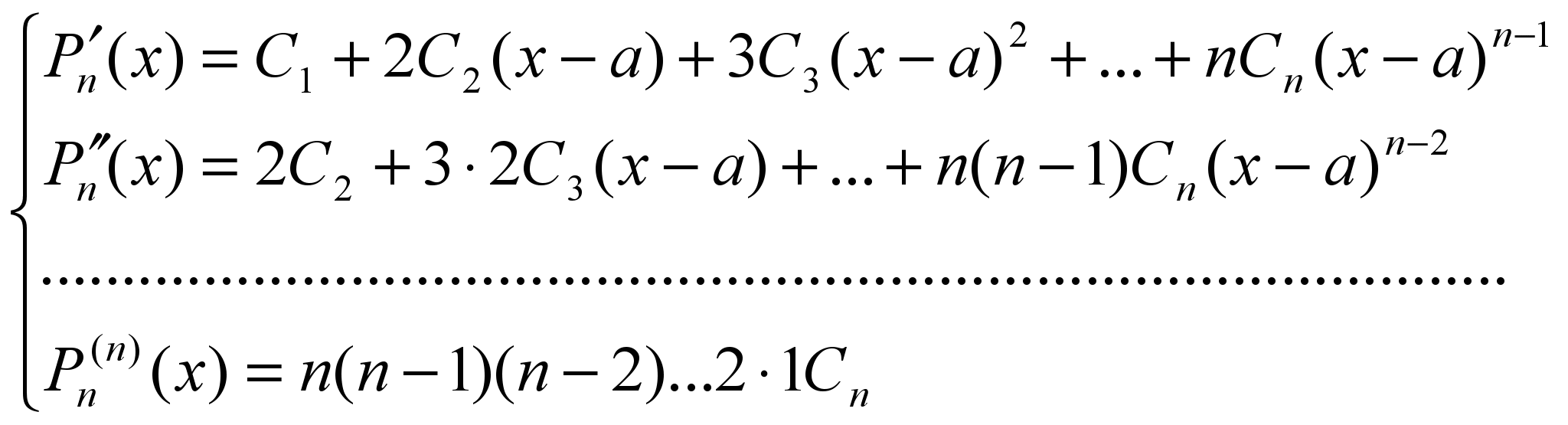 (3)
Решение
этой системы при х = а не вызывает
затруднений, получаем:
(3)
Решение
этой системы при х = а не вызывает
затруднений, получаем:![]()
![]()
![]()
![]() …………………….
…………………….![]() Подставляя
полученные значения Ci в формулу (2),
получаем:
Подставляя
полученные значения Ci в формулу (2),
получаем:![]() Как
было замечено выше, многочлен не точно
совпадает с функцией f(x), т.е. отличается
от нее на некоторую величину. Обозначим
эту величину Rn+1(x). Тогда:
Как
было замечено выше, многочлен не точно
совпадает с функцией f(x), т.е. отличается
от нее на некоторую величину. Обозначим
эту величину Rn+1(x). Тогда:
f(x) = Pn(x) + Rn+1(x) Теорема доказана.
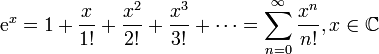
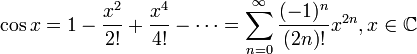
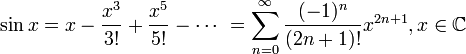
![]() для
всех
для
всех
![]()
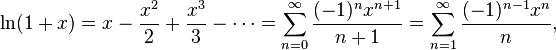 для
всех
для
всех
![]()
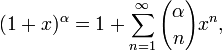 для
всех
для
всех
![]() и
всех комплексных
и
всех комплексных![]() где
где