38. Интегрирование линейных оду первого порядка и уравнения Бернулли.

ДУ первого порядка называется линейным, если неизвестная функция y(x) и её производная y’(x) входят в уравнение в первой степени: . P(x), Q(x) – непрерывные функции. Уравнение однородное, если Q(x)=0.

Форма вариации производной постоянной: (1), обнуляем правую часть

. Общее решение уравнения:. Находим производную. Подставим y и y’ в уравнение (1):

, :.

Уравнения Бернулли имеют следующий вид:

Принцип решения:

Если обозначить за Z(x), то. Отсюда. Подставим это выражение выше и получим:

Получили дифференциальное линейное уравнение, принцип решения которого рассмотрен выше.

Пример: ,,

39. Интегрирование оду первого порядка в полярных дифференциалах. Интегрирующий множитель.

Интегрирование ОДУ первого порядка в полных дифференциалах. Интегрирующий множитель.

Дано уравнение вида

Если левая часть есть дифференциал некоторой функции u(x,y): – общий интеграл уравнения; если, а, то критерий полного дифференциала.

Предположим, что критерий выполняется. Найдём эту функцию u. Пусть , тогда. Так как, то. Отсюда находится φ'(y).

Пример: +

Интегрирующий множитель.

– неполный дифференциал.

Существует ли функция (интегрирующий множитель) по умножению на которую (*) станет полным дифференциалом?

Если найдены два интегрирующих множителя и, то– решение.

Если зависит только от x

Пример:

;

Интегрирующие комбинации:

40. Дифференциальные уравнения первого порядка, неразрешенные относительно производной. Метод введения параметра.

Уравнения, не разрешённые относительно производной, выглядят так: .

Уравнения первого порядка n-ой степени решаются так:

Если из уравнения y можно выразить, то есть, то это решается методом введения параметра, а именно: Обозначим, получим:

Продифференцируем по x:

Получили уравнение, разрешённое относительно производной. p(x,C) подставляем в (*), получим: . Это и будет решение.

Рассмотрим теперь случай, когда из уравнения можно явно выразить x, то есть. Вводим параметр, получаем. Дифференцируем по y обе части:

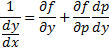
Мы получили уравнение, разрешённое относительно производной . В итоге получаем:.

Уравнение Лагранжа – это уравнение, линейное относительно x и y, оно имеет вид: . Уравнения Лагранжа ВСЕГДА интегрируется в квадратурах.

Принцип решения: Вводим параметр , получаем:

Пусть , поделим всё выражение на A(p):

Продифференцируем по x:

Получили линейное уравнение первого порядка. Отсюда находим .

В итоге решение в параметрическом виде:

Отдельно рассмотрим случай, когда :

Если это тождество, то есть , то:

Если это не тождество, а уравнение с корнями: например, p0 – корень, то есть , тогда– решение.

Частный случай уравнения Лагранжа – это уравнение Клеро. Это когда уравнение Лагранжа имеет следующий вид: . Принцип решения: Вводим параметр, получаем. Дифференцируем по x, получаем:

Общее решение уравнения Клеро:

Здесь – семейство всевозможных кривых;– огибающая этого семейства, тоже является решением и называется особое решение.