
- •Министерство образования и науки Российской федерации
- •Часть I. Механика
- •Тема 1. Кинематика поступательного и вращательного движения. Кинематика поступательного движения
- •Кинематика вращательного движения
- •Тема 2. Динамика поступательного движения. Законы Ньютона
- •Тема 3. Работа. Кинетическая, потенциальная и полная энергия
- •Тема 4. Момент инерции твердого тела. Теорема Штейнера
- •Тема 5. Кинетическая энергия и работа вращательного движения Уравнение динамики вращательного движения твердого тела
- •Тема 6. Момент импульса. Закон сохранения момента импульса
- •Тема 7. Механические колебания. Пружинный маятник
- •Тема 8. Гармонические колебания физического маятника
- •Тема 9. Механические волны
- •Тема 10. Механика жидкости. Уравнение Бернулли
- •Часть II. Молекулярная физика и термодинамика
- •Тема 1. Уравнение состояния идеального газа.
- •Тема 2. Термодинамические процессы. Изопроцессы.
- •Тема 3. Основное уравнение молекулярно-кинетической теории идеального газа.
- •Тема 4. Распределение молекул идеального газа по скоростям.
- •Тема 5. Барометрическая формула. Распределение Больцмана.
- •Тема 6. Явления переноса (диффузия, теплопроводность, вязкость).
- •Тема 7. Первое начало термодинамики. Внутренняя энергия. Работа. Применение первого начала термодинамики к изопроцессам.
- •Тема 8. Теплоемкость газа при изопроцессах. Уравнение Майера.
- •Тема 9. Адиабатический процесс.
- •Тема 10. Обратимый и необратимый процессы. Круговой процесс. Тепловая машина и цикл Карно.
- •Часть III. Электричество и магнетизм
- •Тема 2. Работа сил электростатического поля. Потенциал
- •Циркуляцией вектора напряженности электростатического поляпо произвольному замкнутому контуру l называется интеграл
- •Связь между напряженностью и потенциалом электростатического поля
- •Тема 4. Действие магнитного поля на проводник с током (закон Ампера) и на движущийся заряд (сила Лоренца)
- •Тема. 5. Магнитный поток. Теорема Гаусса для магнитного поля
- •Теорема Гаусса для магнитного поля
- •Тема. 6. Явление электромагнитной индукции. Закон Фарадея
- •Тема 7. Циркуляция вектора магнитной индукции
- •Тема 8. Уравнения Максвелла для стационарных электрического и магнитного полей
- •I. ; II. ;
- •III. ; IV. .
- •Тема 8.Уравнения Максвелла для электромагнитного поля
- •I. ; II. ;
- •Тема 9. Электромагнитные колебания в колебательном контуре
- •Тема 10. Электромагнитные волны
- •Часть IV.Волновая и квантовая оптика
- •Тема 1. Волновая теория света. Интерференция света
- •Условия интерференционного максимума и минимума
- •Тема 2. Дифракция света. Дифракция Френеля
- •Тема 3. Дифракция Фраунгофера
- •Тема 4. Дифракция рентгеновских лучей на кристаллах
- •Глава 5. Дисперсия и поляризация света
- •Тема 6. Корпускулярная оптика
- •Тема7. Тепловое излучение
- •Тема 8. Квантовая физика атома. Постулаты Бора
- •По теории Бора полная энергия электрона на n-ой орбите атома водорода:
Тема 8. Уравнения Максвелла для стационарных электрического и магнитного полей
В случае стационарных (то есть неменяющихся во времени) электрического и магнитного полей, происхождение которых связано с покоящимися зарядами для электрического поля и со стационарными токами для магнитного поля, эти поля являются независимыми друг от друга, что позволяет рассматривать их отдельно друг от друга.
Уравнения Максвелла – это система уравнений, описывающих природу происхождения и свойства электрического и магнитного полей.
Уравнения Максвелла для стационарных полей:
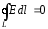 ,
то есть циркуляция вектора напряженности
,
то есть циркуляция вектора напряженности
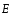 электростатического поля по произвольному
замкнутому контуруL
равна
нулю, что является признаком потенциального
силового
поля и означает, что силовые линии
электростатического поля не являются
замкнутыми, они начинаются и заканчиваются
на зарядах или же уходят в бесконечность.
электростатического поля по произвольному
замкнутому контуруL
равна
нулю, что является признаком потенциального
силового
поля и означает, что силовые линии
электростатического поля не являются
замкнутыми, они начинаются и заканчиваются
на зарядах или же уходят в бесконечность.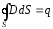 ,
то есть поток вектора смещения
,
то есть поток вектора смещения
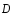 электростатического поля через
произвольную замкнутую поверхностьS
равен алгебраической сумме заключенных
внутри этой поверхности зарядов q
(q
–
заряд, являющийся источником
электростатического
поля).
электростатического поля через
произвольную замкнутую поверхностьS
равен алгебраической сумме заключенных
внутри этой поверхности зарядов q
(q
–
заряд, являющийся источником
электростатического
поля). 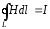 ,
то есть циркуляция вектора
,
то есть циркуляция вектора
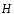 по произвольному замкнутому контуруL
равна алгебраической сумме токов I,
охватываемых этим контуром
L
(I
– стационарный ток, являющийся источником
постоянного
магнитного
поля).
по произвольному замкнутому контуруL
равна алгебраической сумме токов I,
охватываемых этим контуром
L
(I
– стационарный ток, являющийся источником
постоянного
магнитного
поля).
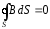 ,
то есть поток вектора индукции
,
то есть поток вектора индукции
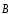 магнитного поля через произвольную
замкнутую поверхность
S
равен нулю.
магнитного поля через произвольную
замкнутую поверхность
S
равен нулю.
Таким образом, уравнения Максвелла для стационарных полей:
I. ; II. ;
III. ; IV. .
Векторные
характеристики электростатического
поля
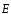 и
и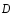 связаны между собой следующим соотношением:
связаны между собой следующим соотношением:
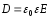 ,
,
где
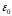 – электрическая постоянная,
e
– диэлектрическая
проницаемость среды.
– электрическая постоянная,
e
– диэлектрическая
проницаемость среды.
Векторные
характеристики магнитного поля
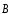 и
и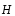 связаны
между собой следующим соотношением:
связаны
между собой следующим соотношением:
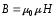 ,
,
где
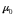 – магнитная постоянная,
– магнитная постоянная,
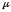 –магнитная
проницаемость среды.
–магнитная
проницаемость среды.
Тема 8.Уравнения Максвелла для электромагнитного поля
Согласно теории Максвелла для электромагнитного поляв случае нестационарных (то есть, изменяющихся во времени) электрического и магнитного полей, источниками электрического поля могут быть либо электрические заряды, либо изменяющееся во времени магнитное поле, а источниками магнитного поля могут быть либо движущиеся электрические заряды (электрические токи), либо переменное электрическое поле.
В отличие от стационарных полей переменные электрическое и магнитное поля не являются независимыми друг от друга и рассматриваются как электромагнитное поле.
Уравнения Максвелла, как система уравнений, описывающих природу происхождения и свойства электрического и магнитного полей в случае электромагнитного поля имеет вид:
I.
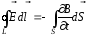 , то есть циркуляция вектора напряженности
электрического поля определяется
скоростью изменения вектора индукции
магнитного поля
, то есть циркуляция вектора напряженности
электрического поля определяется
скоростью изменения вектора индукции
магнитного поля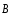 (
(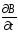 -
скорость изменения вектора индукции
-
скорость изменения вектора индукции
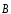 ).
).
Это уравнение показывает, что источниками электрического поля могут быть не только электрические заряды, но и изменяющиеся во времени магнитные поля.
II.
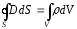 , то есть поток вектора электрического
смещения
, то есть поток вектора электрического
смещения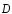 через произвольную замкнутую поверхностьS
, равен алгебраической сумме зарядов,
заключенных внутри объема
V,
ограниченного данной замкнутой
поверхностью
S
(r
-
объемная плотность заряда).
через произвольную замкнутую поверхностьS
, равен алгебраической сумме зарядов,
заключенных внутри объема
V,
ограниченного данной замкнутой
поверхностью
S
(r
-
объемная плотность заряда).
III.
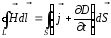 , то есть циркуляция вектора напряженности
, то есть циркуляция вектора напряженности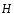 по произвольному замкнутому контуруL
определяется
полным током Iполн.,
пронизывающим поверхность S,
ограниченную данным контуром L.
по произвольному замкнутому контуруL
определяется
полным током Iполн.,
пронизывающим поверхность S,
ограниченную данным контуром L.
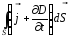 -
полный ток
Iполн
, складывающийся из тока проводимости
I
и
тока
смещения Iсм.,
то есть
Iполн.
=
I
+ Iсм.
.
-
полный ток
Iполн
, складывающийся из тока проводимости
I
и
тока
смещения Iсм.,
то есть
Iполн.
=
I
+ Iсм.
.
Суммарный
ток проводимости I
определяется в общем случае через
поверхностную плотность тока j
(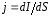 )
интегрированием, то есть
)
интегрированием, то есть
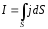 .
.
Ток смещения Iсм , пронизывающий поверхность S , определяется в общем
случае
через поверхностную плотность тока
смещения
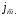 (
(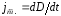 )
интегрированием, то есть :
)
интегрированием, то есть :
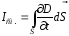 .
.
Введенное
Максвеллом понятие «тока смещения»,
величина которого определяется скоростью
изменения вектора электрического
смещения
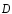 , то есть величиной
, то есть величиной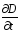 , показывает, что магнитные поля могут
возбуждаться не только движущимися
зарядами (электрическими токами
проводимости), но и переменными
электрическими полями.
, показывает, что магнитные поля могут
возбуждаться не только движущимися
зарядами (электрическими токами
проводимости), но и переменными
электрическими полями.
IV.
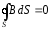 , то есть поток вектора индукции
, то есть поток вектора индукции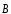 магнитного поля через произвольную
замкнутую поверхность
S
равен нулю.
магнитного поля через произвольную
замкнутую поверхность
S
равен нулю.
Таким образом, уравнения Максвелла для электромагнитного поля:
