
- •Министерство образования и науки Российской федерации
- •Часть I. Механика
- •Тема 1. Кинематика поступательного и вращательного движения. Кинематика поступательного движения
- •Кинематика вращательного движения
- •Тема 2. Динамика поступательного движения. Законы Ньютона
- •Тема 3. Работа. Кинетическая, потенциальная и полная энергия
- •Тема 4. Момент инерции твердого тела. Теорема Штейнера
- •Тема 5. Кинетическая энергия и работа вращательного движения Уравнение динамики вращательного движения твердого тела
- •Тема 6. Момент импульса. Закон сохранения момента импульса
- •Тема 7. Механические колебания. Пружинный маятник
- •Тема 8. Гармонические колебания физического маятника
- •Тема 9. Механические волны
- •Тема 10. Механика жидкости. Уравнение Бернулли
- •Часть II. Молекулярная физика и термодинамика
- •Тема 1. Уравнение состояния идеального газа.
- •Тема 2. Термодинамические процессы. Изопроцессы.
- •Тема 3. Основное уравнение молекулярно-кинетической теории идеального газа.
- •Тема 4. Распределение молекул идеального газа по скоростям.
- •Тема 5. Барометрическая формула. Распределение Больцмана.
- •Тема 6. Явления переноса (диффузия, теплопроводность, вязкость).
- •Тема 7. Первое начало термодинамики. Внутренняя энергия. Работа. Применение первого начала термодинамики к изопроцессам.
- •Тема 8. Теплоемкость газа при изопроцессах. Уравнение Майера.
- •Тема 9. Адиабатический процесс.
- •Тема 10. Обратимый и необратимый процессы. Круговой процесс. Тепловая машина и цикл Карно.
- •Часть III. Электричество и магнетизм
- •Тема 2. Работа сил электростатического поля. Потенциал
- •Циркуляцией вектора напряженности электростатического поляпо произвольному замкнутому контуру l называется интеграл
- •Связь между напряженностью и потенциалом электростатического поля
- •Тема 4. Действие магнитного поля на проводник с током (закон Ампера) и на движущийся заряд (сила Лоренца)
- •Тема. 5. Магнитный поток. Теорема Гаусса для магнитного поля
- •Теорема Гаусса для магнитного поля
- •Тема. 6. Явление электромагнитной индукции. Закон Фарадея
- •Тема 7. Циркуляция вектора магнитной индукции
- •Тема 8. Уравнения Максвелла для стационарных электрического и магнитного полей
- •I. ; II. ;
- •III. ; IV. .
- •Тема 8.Уравнения Максвелла для электромагнитного поля
- •I. ; II. ;
- •Тема 9. Электромагнитные колебания в колебательном контуре
- •Тема 10. Электромагнитные волны
- •Часть IV.Волновая и квантовая оптика
- •Тема 1. Волновая теория света. Интерференция света
- •Условия интерференционного максимума и минимума
- •Тема 2. Дифракция света. Дифракция Френеля
- •Тема 3. Дифракция Фраунгофера
- •Тема 4. Дифракция рентгеновских лучей на кристаллах
- •Глава 5. Дисперсия и поляризация света
- •Тема 6. Корпускулярная оптика
- •Тема7. Тепловое излучение
- •Тема 8. Квантовая физика атома. Постулаты Бора
- •По теории Бора полная энергия электрона на n-ой орбите атома водорода:
Часть III. Электричество и магнетизм
ЭЛЕКТРОСТАТИКА
Тема 1. Теорема Остроградского-Гаусса для электростатического поля
Электростатическое поле – это особый вид материи, с помощью которой происходит взаимодействие заряженных тел.
Точечным называется заряд, сосредоточенный на теле, размерами которого можно пренебречь по сравнению с расстоянием до других заряженных тел, с которыми он взаимодействует.
Закон Кулона: сила взаимодействияFмежду двумя неподвижными точечными зарядами q1иq2прямопропорциональна величинам этих зарядов и обратно пропорциональна квадрату расстоянияrмежду ними:
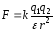 ,
,
где
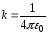 (e0–
электрическая постоянная);
(e0–
электрическая постоянная);
e– диэлектрическая проницаемость среды, показывающая во сколько раз сила взаимодействия зарядов в данной среде меньше, чем в вакууме.
Кулоновская
сила
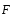 направлена по прямой, соединяющей
взаимодействующие точечные заряды,
соответствует притяжению в случае
разноименных зарядов и отталкиванию в
случае одноименных зарядов. Электрические
поля, которые создаются неподвижными
электрическими зарядами, называютсяэлектростатическими.
направлена по прямой, соединяющей
взаимодействующие точечные заряды,
соответствует притяжению в случае
разноименных зарядов и отталкиванию в
случае одноименных зарядов. Электрические
поля, которые создаются неподвижными
электрическими зарядами, называютсяэлектростатическими.
Для
обнаружения и опытного исследования
электростатического поля можно
использовать пробный точечный заряд
q0 . Если этот
заряд поместить в какую- либо точку
электростатического поля, то на
него будет действовать сила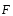 ,
величина и направление которой определяет
силовую характеристику электростатического
поля, носящую название напряженности
электростатического поля.
,
величина и направление которой определяет
силовую характеристику электростатического
поля, носящую название напряженности
электростатического поля.
Напряженность
электростатического поляв данной
точке есть физическая величина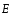 ,
определяемая силой, действующей на
пробный точечный положительный заряд
q0 , помещенный
в эту точку поля, то есть:
,
определяемая силой, действующей на
пробный точечный положительный заряд
q0 , помещенный
в эту точку поля, то есть:
 .
.
Напряжённость электростатического поля, создаваемого точечным зарядом q в любой точке поля, находящейся на расстоянии r от этого заряда:
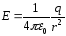 .
.
Электростатическое
поле может быть изображено графически
с помощью силовых линий. Силовая
линия —это такая линия, касательная
в каждой точке к которой совпадает по
направлению с вектором напряженности
электростатическго поля в данной точке
(рис. 1, 2).
Рис. 1 Рис. 2
Если поле создается точечным зарядом, то силовые линии – это радиальные прямые, выходящие из положительного заряда (рис. 2, а), и входящие в отрицательный заряд (рис. 2,б).
С
помощью силовых линий можно характеризовать
не только направление, но и величину
напряженности электростатического
поля, связывая её с густотой силовых
линий. Большей густоте силовых линий
соответствует большая величина
напряженности (рис. 1, 2). Количественно
числу силовых линий, пронизывающих
единичную площадку, расположенную
перпендикулярно силовым линиям, ставится
в соответствие величина напряженности
электростатического поля. В этом случае
определенному заряду q, создающему
поле, соответствует определенное числоNсиловых линий,
выходящих (для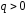 )
из заряда или входящих (для
)
из заряда или входящих (для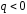 )
в заряд, а именно:
)
в заряд, а именно: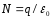 .
.
Поток
вектора напряженностиэлектростатического
поля
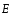 через произвольную площадкуSхарактеризуется числом силовых линий,
пронизывающих данную площадкуS.
через произвольную площадкуSхарактеризуется числом силовых линий,
пронизывающих данную площадкуS.
Если
площадка S
перпендикулярна силовым линиям (рис.
3), то потокФЕвектора
напряженности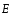 через данную площадкуS
:
через данную площадкуS
: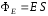 .
.
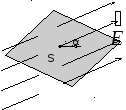

Рис. 3 Рис. 4
Если
же площадка S
расположена неперпендикулярно силовым
линиям электро-статического поля (рис.
4), то поток вектора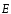 через данную площадкуS
:
через данную площадкуS
:
Рис. 3
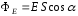 ,
,
где
α– угол между векторами напряженности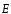 и нормали
и нормали к площадкеS.
к площадкеS.
Для
того, чтобы найти поток ФЕ
вектора напряженности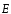 через произвольную поверхностьS,
необходимо разбить эту поверхность
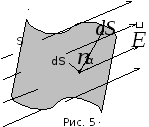
на элементарные площадкиdS
(рис. 5), определить элементарный
потокdФЕчерез каждую элементарную площадкуdSпо формуле:
через произвольную поверхностьS,
необходимо разбить эту поверхность
на элементарные площадкиdS
(рис. 5), определить элементарный
потокdФЕчерез каждую элементарную площадкуdSпо формуле: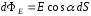 ,
,
а затем все эти элементарные потоки dФЕсложить, что приводит к интегрированию:
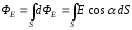 ,
,
где
α– угол между векторами напряженности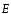 и нормали
и нормали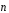 к данной элементарной площадкеdS
.
к данной элементарной площадкеdS
.
Рис. 7
Если
ввести вектор
 (рис. 5) как вектор, равный по величине
площади площадкиdSи направленный по вектору нормали
(рис. 5) как вектор, равный по величине
площади площадкиdSи направленный по вектору нормали

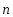 к площадкеdS , то
величина
к площадкеdS , то
величина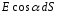 ,
гдеa
– угол между векторами
,
гдеa
– угол между векторами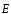 и
и может быть записана в виде скалярного
произведения векторов
может быть записана в виде скалярного
произведения векторов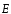 и
и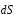 ,
то есть, как
,
то есть, как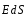 ,
а полученное соотношение для потока
вектора
,
а полученное соотношение для потока
вектора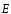 примет вид:
примет вид:
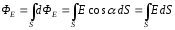 .
.
Теорема Остроградского - Гаусса для электростатического поля.Теорема Остроградского - Гаусса для электростатического поля связывает между собой величину потока ФЕвектора напряженности электростатического поля в вакуумечерез произвольную замкнутую поверхностьS с величиной заряда q,заключенного внутри даннойзамкнутой поверхностиS (рис. 6).
Поскольку все
силовые линии, выходящие из заряда (для
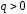 )
или входящие в заряд (для
)
или входящие в заряд (для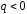 ),
пронизывают произвольную замкнутую
поверхностьS,
охватывающую этот заряд (рис. 6), то
величина потокаФЕвектора
напряженности электростатического
поля через эту произвольную замкнутую
поверхностьS будет
определяться числомNсиловых линий, выходящих из заряда (для
),
пронизывают произвольную замкнутую
поверхностьS,
охватывающую этот заряд (рис. 6), то
величина потокаФЕвектора
напряженности электростатического
поля через эту произвольную замкнутую
поверхностьS будет
определяться числомNсиловых линий, выходящих из заряда (для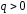 )
или входящих в заряд (для
)
или входящих в заряд (для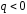 ):
):
Рис. 6
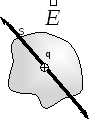
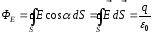 .
.
Это соотношение есть теорема Остроградского-Гаусса для электростатического поля.
Так как поток считается положительным, если силовые линии выходят из поверхности S, и отрицательным для линий, входящих в поверхность S, то в случае, если внутри произвольной замкнутой поверхности Sнаходится не один, а несколько (n) разноименных зарялов, тотеорема Остроградского - Гауссадля электростатического поля формулируется следующим образом:
поток вектора напряженности электростатического поля в вакууме через произвольную замкнутую поверхность равен алгебраической сумме заключенных внутри этой поверхности зарядов, деленной на e0 :
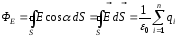 .
.
В
общем случае электрические заряды могут
быть распределены внутри объёма,
ограниченного замкнутой поверхностью
S, с некоторой
объемной плотностью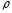 (
(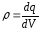 ),различной в разных местах пространства.
Тогда суммарный заряд, заключенный
внутри этой замкнутой поверхностиS,
охватывающей объемV, равен:
),различной в разных местах пространства.
Тогда суммарный заряд, заключенный
внутри этой замкнутой поверхностиS,
охватывающей объемV, равен: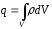 .
.
В таком случае теорема Остроградского - Гауссаприобретает вид:
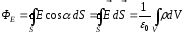 .
.
Напряженность
электростатического поля зависит от
диэлектрических свойств среды. В
диэлектрике напряженность поля меньше,
чем напряженность внешнего
электростатического поля в вакууме, в
котором находится диэлектрик, вe
раз (e –
диэлектрическая проницаемость среды),
а модуль вектора ,
переходя через границу диэлектриков,
скачкообразно изменяется. Поэтому
для характеристики электростатического
поля, кроме вектора напряженности
,
переходя через границу диэлектриков,
скачкообразно изменяется. Поэтому
для характеристики электростатического
поля, кроме вектора напряженности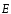 ,
введен вектор электрического смещения
,
введен вектор электрического смещения
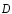 ,модуль которого не изменяется при
переходе из одной диэлектрической среды
в другую.
,модуль которого не изменяется при
переходе из одной диэлектрической среды
в другую.
Вектор
электрического смещения
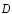 по определению:
по определению: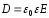 .
.
Используя
то, что в вакууме
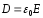 ,теорема Остроградского-Гауссадля
электростатического поля может быть
переформулирована следующим образом:
,теорема Остроградского-Гауссадля
электростатического поля может быть
переформулирована следующим образом:
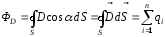 ,
,
то
есть поток вектора смещения
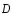 электростатического поля через
произвольную замкнутую поверхностьSравен алгебраической
сумме заключенных внутри этой поверхности
зарядов.
электростатического поля через
произвольную замкнутую поверхностьSравен алгебраической
сумме заключенных внутри этой поверхности
зарядов.
В
случае, если электрические заряды
распределены внутри объёма V,
ограни-ченного замкнутой поверхностью
S, с некоторой
объемной плотностью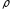 ,теорема Остроградского-Гауссадля
электростатического поля может
быть переформулирована сдедующим
образом:
,теорема Остроградского-Гауссадля
электростатического поля может
быть переформулирована сдедующим
образом:
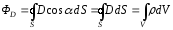 .
.
