Решение

Зная напряжение U₁ и воспользовавшись В.А.Х. определим величину тока на 1 и 2 нелинейных элементах:I₁= 0,25 (А). Напряжение на втором нелинейном элементе также будет равно 30 (В).

Напряжение параллельного участка U_авравно 60 (В). ТокI₂ определится как отношение напряженияU_ав к сопротивлениюr :

Ток в неразветвленной части цепи определится как сумма токов на нелинейных элементах I₁и на сопротивленииr:

Ответ: I= 1,45A.

Задача 2.5

Лампа накаливания В.А.Х. которой представлена на рисунке 2.6, последовательно соединена с линейным сопротивлениемR₀ = 100 (Ом). Какова будет величина токаI, протекающего в цепи, если напряжение, приложенное к зажимам цепиU= 100 (В).

а) б)

Рисунок 2.5. – а) Схема электрической цепи; б) В.А.Х. лампы накаливания

Решение

Точку рабочего режима можно определить пересечением двух вольт-амперных характеристик: ВАХ лампы и обратной ВАХ сопротивления R₀. Обратную ВАХ линейного сопротивленияR₀ строят по двум точкам: соответствующим режимам холостого хода и короткого замыкания.

Для решения данной задачи необходимо провести опыт холостого хода, определив напряжение U_хх и опыт короткого замыкания, определив токI_к. Схема электрической цепи для двух опытов будет выглядеть следующим образом:

Рисунок 2.6 – Схема электрической цепи для опыта холостого хода и короткого замыкания

U_хх = 100 (В);I_хх= 0(А).U_кз= 0 (В);По полученным значениямU_хх иI_к построим обратную В.А.Х. для линейного элементаR₀ I(-U_R0).Точка пересечения двух В.А.Х. (линейного элемента и лампочки) есть решение задачи, откуда значение токаI= 0,5 (A), напряжения на элементахU_Л = 50 (В); U_R0= 50 (В).

Ответ: I= 0,5 A.

Задача 2.6

Нелинейное сопротивление, В.А.Х. которого представлена на рисунке 2.7, и линейное сопротивление R₀ = 30 (Ом), включены последовательно. Напряжение на линейном элементеU₀ = 15 (В). Чему равно напряжение цепиU.

а) б)

Рисунок 2.7 – Схема электрической цепи и В.А.Х. нелинейного сопротивления

Решение

Зная напряжение U₀ и сопротивлениеR₀определим величину тока:Поскольку сопротивления соединены последовательно, ток в цепи будет равен 0,5 (А). ИспользуяВ.А.Х. определим напряжение на нелинейном элементеU₁= 35 (В). Общее напряжение цепиU равно сумме напряжений на нелинейном элементе U₁и линейномU₀:

Ответ: U = 50 В.

Задача 2.7

В.А.Х. нелинейного элемента задана на рисунке 2.8. пользуясь методом эквивалентного генератора, определить токI, проходящий через нелинейный элемент, еслиЕ= 40 (В),R= 6 (Ом).

а) б)

Рисунок 2.8 – а) Схема электрической цепи; б) В.А. Х. нелинейного элемента

Решение

Эквивалентное линейное сопротивление цепи: Схема расчетной цепи сR_Э представлена на рисунке 2.9:

Рисунок 2.9 – Схема замещения электрической цепи

Для построения обратной В.А.Х. линейного сопротивленияR_Э определяем напряжение холостого хода, и ток короткого замыкания.

;;.

Из точки пересечения В.А.Х.нелинейного элемента иВ.А.Х.линейного элемента проведем перпендикуляр на ось ординат, и получим значение токаI= 2,5 (А);U_нэ= 15 (В);U_Rэ= 25 (В).

Ответ: I= 2,5 А; U_нэ= 15 (В);U_Rэ= 25 (В).

Задача 2.9

В схеме, представленной на рисунке 2.14., Е= 40 В,I_К = 0,2 А, приведеныВ.А.Х.нелинейных элементов. Определить токи и напряжения нелинейных элементов.

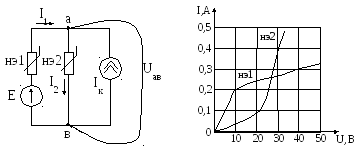
Рисунок 2.14 – Схема электрической цепи и В.А.Х. нелинейных элементов

Решение

Для данной электрической цепи составим уравнения по второму закону Кирхгофа, и определим напряжение U_ав :После графически решим уравнение, составленное по первому закону Кирхгофа:

Точка пересечения определяет напряжение U_ав=U₂ = 30 В, и ток

I₁= 0,2 А (рис.2.15). На основании уравнений, составленных по второму закону Кирхгофа и характеристик нелинейных элементов находим:U₁= 10 В;I₂= 0,4 А.

Рисунок 2.15 – Графическое определение напряжения U_ав

Задача 2.10

Линейное сопротивление R= 300 (Ом) и два нелинейных элемента соединены параллельно. Заданы вольт-амперные характеристики нелинейных элементов и ток первого элементаI₁= 0,8 (А) (рис. 2.16). Чему равен токIв неразветвленной части цепи?

а) б)

Рисунок 2.16 – а) Схема электрической цепи; б) В.А.Х. нелинейных элементов

Решение

Зная значение тока I_1, используяВ.А.Х. I₁(U) или используяВАХнэ1 определим напряжение на первом нелинейном элементеU₁= 25 (В). Поскольку элементы соединены параллельно, тоU₁= 25 (В) является общим напряжением цепи U₁= U. ИспользуяВ.А.Х.I₂(U)или используяВАХнэ2 и зная величину общего напряжения цепиU, определим ток на втором нелинейном элементеI₂ = 0,4 (А).

Ток на активном сопротивлении R :Ток в неразветвленной части цепи Iопределится как сумма токов на каждом из элементов:

Ответ: I = 1,28 А.

Задача 2.11

Два одинаковых нелинейных элемента и линейное сопротивление

R= 3 Ом соединены, как показано на рисунке 2.17.В.А.Х.каждого из нелинейных элементов приведена также на рисунке 2.17. Определить общее напряжение, приложенное к цепи, если ток на первом нелинейном элементеI₁= 5 А.

Рисунок 2.17 – схема электрической цепи и В.А.Х. нелинейных элементов

Решение

Зная величину тока I₁ используяВ.А.Х. определим напряжение на первом нелинейном элементеU₁= 7 (В). Поскольку нелинейный элемент и линейное сопротивление соединены последовательно, то напряжение на линейном сопротивленииR определится следующим образом:

Напряжение приложенное к цепи определим, как сумму напряжений на нелинейном и линейном элементе:

Ответ: U= 22 В.

Задача 2.12

У двух нелинейных элементов В.А.Х.заданы в виде выражений:,. При каком значении напряжения статические сопротивления элементов будут равны.

Решение

Статическое сопротивление нелинейного элемента в любой точке его ВАХ_, определяется как отношение напряжения к току:. Определим статические сопротивления элементов, для одного и того же напряженияUи приравняем их друг другу:;.

Ответ:

У двух нелинейных элементов В.А.Х.заданы в виде выражений:,. При каком значении напряжения дифференциальные сопротивления элементов будут равны.

Решение

Дифференциальное сопротивление R_диф, определяется как отношение дифференциала напряжения к дифференциалу тока:. Определим дифференциальные проводимости элементов, и приравняем их:

Ответ:

Задача 2.13

Последовательно с лампой накаливания включено линейное сопротивление r= 125 (Ом) (рис.2.18). Каким будет статическое сопротивление лампы, при условии, что напряжение на лампе в два раза больше, чем напряжение на линейном элементе.

Рисунок 2.18 – Схема электрической цепи

Решение

Статическое сопротивление лампы определим по формуле: Элементы соединены последовательно, при одном токе напряжение на лампеU₁в два раза больше чем на линейном сопротивлении r, значит статическое сопротивление лампы будет также в два раза больше линейного сопротивления, и будет равно 250 (Ом).

Ответ: 250 Ом.

Задача 2.14

Вольт-амперная характеристика U=f(I) имеет максимум при токе 5 А и напряжении 350 В. Чему равно дифференциальное сопротивление элемента в области максимального значения напряжения?

Решение

Дифференциальное сопротивление определяется по формуле: Так как дифференциал постоянной напряжения равен 0, то и в момент максима кратковременно изменения напряжения не происходит:

dU= 0, дифференциальное сопротивление равно нулю.

Ответ:

Задача 2.15

Параллельно с лампой накаливания включено линейное сопротивление R₀= 100 (Ом) (рис.2.19). Приложенное к цепи напряжениеU= 150 (В), а потребляемый цепью токI= 3,5 (А). Чему равно статистическое сопротивление лампы?

Рисунок 2.19 – Схема электрической цепи к задаче 2.15

Решение

Зная общее напряжение цепи Uи линейное сопротивление R₀ определим ток:ТокI₁определим как разницу между общим током в цепи и токомI₂:Статическое сопротивление лампы определим как:

Ответ:

Задача 2.16

Два нелинейных элемента вольт-амперные характеристики которых приведены на рисунке 2.20, соединены последовательно. Напряжение на первом элементе U₁= 200 (В). Чему равно напряжение цепи?

а) б)

Рисунок 2.20 – а) Схема электрической цепи; б) В.А.Х. нелинейных элементов

Решение

Используя вольт-амперную характеристику, определим ток на первом нелинейном элементе: I₁= 0,3 (А) поскольку нелинейные элементы соединены последовательно, то токI₁ будет одинаковым для всей цепи. Зная значение тока, продолжим наВ.А.Х. отрезок из точкиI₁= 0,3 (А) до пересечения с кривой второго элемента, и получим величину напряженияU₂= 250 (В). Напряжение цепи равно сумме напряжений на двух элементах:

Ответ: U₂= 450 В.

Задача 2.17

Последовательно соединены нелинейное сопротивление и линейное, В.А.Х.нелинейного сопротивления представлена на рисунке 2.22, величина линейного сопротивленияR= 40 (Ом), напряжение на нелинейном элементеU= 50 (В). Определить общее напряжение, приложенное к цепи.

а) б)

Рисунок 2.22 – а) Схема электрической цепи; б) В.А.Х. нелинейного элемента

Решение

Воспользовавшись вольт-амперной характеристикой, определим ток на нелинейном элементе, получим значение тока I₁= 4 (А). Поскольку два сопротивления соединены последовательно, то токI₁будет одинаковым для всей цепи. Напряжение на сопротивленииR

Общее напряжение цепи определим как сумму напряжений на каждом элементе:

Ответ: U= 210 В.

Задача 2.18

На рисунке 2.23 изображены В.А.Х.нелинейных элементов. Какой вид имеет вольт-амперная характеристика лампы накаливания и почему?

Рисунок 2.23 – В.А.Х. нелинейных элементов

Решение

При подключении лампы накаливания к напряжению происходит разогрев спирали. С повышением температуры сопротивление спирали изменяется по нелинейному закону. С достижением установившейся температуры сопротивление спирали (лампы) не изменяется, ВАХстановится прямолинейной. Такому характеру измененияВАХсоответствует кривая «В» (рис. 2.24).

Рисунок 2.24 – В.А.Х. лампы накаливания

На рисунке 2.25 изображены вольт-амперные характеристики пяти нелиненых элементов. Какой из них можно использовать для стабилизации

Рисунок 2.25 – В.А.Х. нелинейных элементов