Задача 1.6

Каким должно быть сопротивление R_X (рис.1.10), чтобы при замыкании рубильникаК токи в цепи не менялись? Задано:R₁= 6 (Ом),

R₂= 3 (Ом),R₃= 8 (Ом),R₄= 1 (Ом),Е₁= 20 (В),Е₂= 25 (В),

Е₃= 30 (В),Е₄= 45(В).

Рисунок 1.10 – Схема цепи к задаче 1.6

Решение

Рассмотрим схему в начальный момент времени, когда ключ К разомкнут. Выбрав произвольно направление обхода, например против часовой стрелки, составим уравнение по 2-му закону Кирхгофа для внешнего контура:

где

После замыкания ключа К, по условию задачи, ток в каждом контуре должен остаться неизменным. Определим токIдля контура с эдсЕ₁ иЕ₃ при замкнутом ключеК:

Теперь из уравнения (*) можно найти сопротивление R_X:

Ответ: R_X = 3(Ом).

Задача 1.7

Что покажет амперметр (рис.1.11) после замыкания ключа К, если до замыкания он показывал 1 (А)? Дано:R₁= 6(Ом),R₂= 2(Ом),

R₃= 3(Ом),R₄= 4(Ом),R₅= 5(Ом).

Рисунок 1.11 – Схема электрической цепи к задаче 1.7

Решение

Эквивалентное сопротивление цепи при разомкнутом ключе

По закону Ома:

При замыкании ключ К шунтирует сопротивлениеR₄. При этом ток через это сопротивление будет равен нулю и в работе цепиR₄ уже не участвует. Эквивалентное сопротивление цепи при замкнутом ключе:

Отсюда:

Ответ: после замыкания ключа Камперметр покажет 1,17 (А).

Задача 1.8

Определить напряжениеU_ab для заданных цепей (рис.1.12)

Рисунок 1.12 – Схемы электрических цепей к задаче 1.8: с ЭДС Е, совпадающей с током I по направлению (а), и с ЭДС Е, направленной встречно току I (б)

Решение

Выражения для напряжения U_ab получим из уравнений, составленных по 2-му закону Кирхгофа для заданных цепей. Контуры, вдоль которых производится обход, могут замыкаться не только по ветвям цепи, но и по векторам напряжений. Для обеих цепей выберем направление обхода по часовой стрелке.

Для первой цепи (рис.1.12,а):

Для второй цепи (рис.1.12,б):

Задача 1.9

Найти потенциалы точек c,dиb, еслиφ_а = 2(В), I= 1 (А),

R₁= 1 (Ом),R₂= 2 (Ом),Е= 5 (В) (рис.1.13)

Рисунок 1.13 – Схема электрической цепи к задаче 1.9

Решение

Для определения потенциала φ_b необходимо вспомнить, чтоU_ba= -U_ab=φ_b -φ_a. очевидно, из этого выражения можно найтиφ_{b при известных} U_ba иφ_а. НайдемU_ba.

По 2-му закону Кирхгофа, при направлении обхода по часовой стрелке, имеем:

Для определения потенциалов указанных точек цепи необходимо помнить, что ток в цепи всегда направлен от более высокого потенциала к более низкому, а острие стрелки ЭДС указывает на положительный

(высокий ) потенциал. Определим потенциалы точек c,dиb:

Напряжение:

Задача 1.10

Определить напряжение U_cb, еслиU_аb= 5 (В),Е= 5(В),

R₁= 1(Ом),R₂= 2(Ом)(рис.1.14).

Рисунок 1.14 – Схема электрической цепи к задаче 1.10

Решение

Так как напряжение U_ab известно, то для определенияU_сb необходимо найти напряжение на резистореR₁.

Из уравнения, составленного по 2-му закону Кирхгофа для участка цепи ab, определим ток I:

Откуда:

Напряжение

Ответ:

Задача 1.11

Чему равны показания вольтметровV₁ иV₂, включенных в цепь постоянного тока (рис.1.15), если вольтметрV₃ показывает 12 (В), а сопротивлениеR= 1О (Ом_? Переходный процесс следует считать завершенным.

Рисунок 1.15 –Схема электрической цепи к задаче 1.11

Решение

Так как переходный процесс завершен, то емкостный элемент Сзаряжен до величины напряжения источника. Показания вольтметраV₂:

U₂ =12(В). Левая обкладка конденсатора заряжена до величины потенциала «+» источника. Следовательно, ток через сопротивлениеRотсутствует. Напряжение U₁:

Ответ: U₁= 0(В), U₂= 12(В).

Задача 1.12

Дано: I_к=1 (А),R₀ = 2 (Ом),R₁ = 5 (Ом),R₂ = 10 (Ом),Е= 25(В) (рис.1.16). Определить напряжениеU_ab.

Рисунок 1.16 – Схема электрической цепи к задаче 1.12

Решение

Рациональнее всего для решения данной задачи применить метод двух узлов, хотя можно использовать и метод непосредственного применения законов Кирхгофа. Последний значительно более трудоемкий.

Определим проводимости первой и второй параллельных ветвей:

Проводимость третьей ветки равна нулю, поскольку источник тока по определению имеет бесконечно большое внутреннее сопротивление.

Напряжение между узлами:

Напряжение U_ab найдем по второму закону Кирхгофа:

Ответ: U_ab = 22 (В).

Задача 1.13

Определить, какие из трех источников ЭДС (рис.1.17) генерируют энергию, а какие потребляют, если R₁= 8 (Ом),R₂= 2 (Ом),R₃= 2 (Ом),

Е₁= 32(В),Е₂= 3(В),Е₃= 2(В). Проверить правильность решения, составив уравнения для баланса мощностей.

Решение

Определим напряжение U_ab по методу двух узлов:

Рисунок 1.17 – Схема электрической цепи к задаче 1.13

Выражение берется со знаком «+», если направление эдсЕ₁ ветви не совпадает с направление напряженияU_ab, и наоборот.

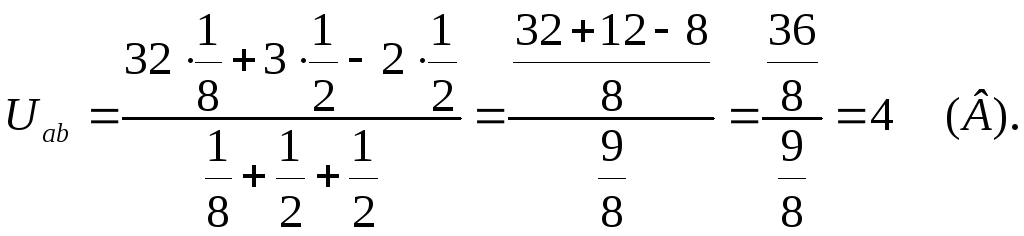
Составим уравнение по второму закону Кирхгофа для каждого из контуров, в которые входят ветви 1,2,3и напряжениеU_ab.Направление обхода выберем по часовой стрелке.

откуда

откуда

откуда

Направление тока I_2, полученное со знаком «-», в действительности противоположно выбранному условному положительному направлению (рис.1.18).

Рисунок 1.18 – Схема электрической цепи с реально протекающими токами

Источник, направление ЭДС которого совпадает с направление реально протекающего через него тока, является генератором. В противном случае он является потребителем.

ЭДС Е₁ иЕ₃ – генерируют энергию, аЕ₂ – потребляет.

Проверим баланс мощностей:

Ответ: Е₁ иЕ₃ – генератор,Е₂ – потребитель.