Уравнение прямой в отрезках

Уравнение (**), где все А, В, С отличны от нуля, можно привести к виду:

Действительно,

Числа а и b имеют простой геометрический смысл: это отрезки осей координат, которые отсекает прямая линия, удовлетворяющая этому уравнению.

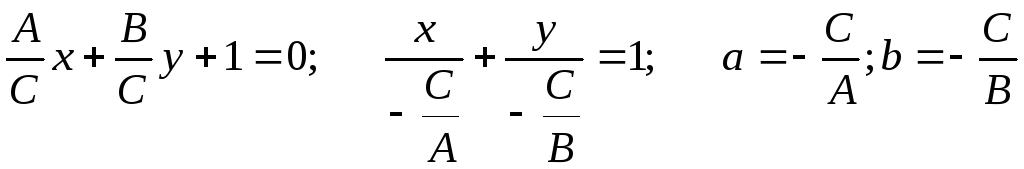
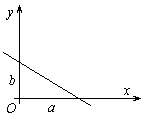
Действительно, при х = 0 :

при у = 0 : х = а

Каноническое уравнение прямой

Определим направляющий вектор прямой, как ненулевой вектор, параллельный данной прямой. Поставим задачу: найти уравнение прямой, проходящей через заданную точку М₁(х₁ ; у₁) и имеющей направляющий вектор .

Очевидно, что точка М(х ; у) лежит на указанной прямой, если векторы ММ₁ = и коллинеарные, т.е. их координаты пропорциональны:

(****)

Это уравнение и называют каноническим уравнением прямой линии.

Отсюда легко найти уравнение прямой, проходящей через две точки М₁(х_1, у₁) и М₂(х_2, у₂). Очевидно, направляющий вектор такой прямой есть

Уравнение, очевидно, есть:

Параметрическое уравнение прямой

Из уравнения (****) можно получить параметрическое уравнение прямой. Действительно, из этого уравнения можно записать:

х - х₁ = l t ; y - y₁ = m t , или

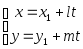
Эту систему легко наглядно представить. Если считать t временем, то координаты х у есть координаты точки, двигающейся по линии с направляющим вектором и имеющей скорость .

Прямая с угловым коэффициентом

Введем понятие угла наклона прямой к оси Ох.

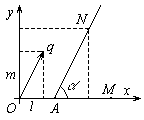
NAM назовем углом наклона прямой к оси Ох. Тангенс угла наклона назовем угловым коэффициентом этой прямой.

k = tg 

Из канонического уравнения прямой линии получим:

:

k = tg  = m/l

Число b представляет собой величину отрезка, отсекаемого на оси Оу этой прямой.

Угол между двумя прямыми

а). Пусть даны две прямые: A₁ x + B₁ y + C₁ = 0 и A₂ x + B₂ y + C₂ = 0

Т.к. нормальным вектором для первой прямой является вектор , а для второй , то задача сводится к определению угла между векторами и . Выполним скалярное произведение двух векторов: получим

Условие параллельности двух прямых, очевидно эквивалентно условию коллинеарности и :

Условие перпендикулярности – равенство нулю скалярного произведения A₁A₂ + B₁B₂=0.

б). Если две прямые заданы своими каноническими уравнениями

и , то поскольку направляющие векторы этих прямых есть и , то аналогично предыдущему имеем:

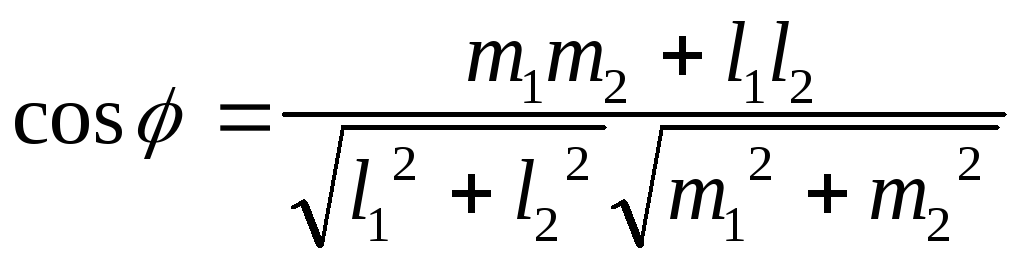
Условие паралельности -

У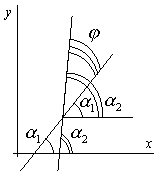словие перпендикулярности -l₁l₂ = m₁m₂.

в). Если две прямые L₁ и L₂ заданы уравнениями с угловыми коэффициентами:

y = k₁ x + b₁ и y = k₂ x + b₂

Из геометрических соображений ясно, что  = ₂ - ₁

Условие паралельности -  = 0, tg  = 0, k₁ = k₂;

Условие перпендикулярности – его можно получить из условия tg   , или 1+ k₁k₂=0, откуда .

Нормированное уравнение прямой

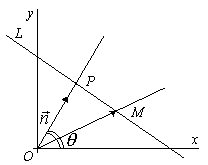
Поставим задачу: выразить уравнение прямой L через два параметра: 1) длину отрезка , где - единичный вектор нормали к прямой 2) угол  между вектором и осью Ох.

Очевидно, .

Точка М(х, у) лежит на прямой L тогда и только тогда, когда проекция на ось, определяемую вектором , равна - длине отрезка , обозначенной за Р.

Если единичный вектор, то в силу определения скалярного произведения, имеем:

Т.е. точка М(х, у) лежит на прямой L тогда и только тогда, когда координаты этой точки удовлетворяют уравнению: .

Это уравнение называется нормированным уравнением прямой.

Как привести уравнение A x + B y + C = 0 к нормированному виду? Так, как уравнения A x + B y + C = 0 и должны определять одну и туже прямую, то должно быть: , или .

Возведем в квадрат и складывая первые два равенства, получим

Знак нужно взять из третьего равенства : поскольку р – расстояние, которое всегда положительно, то знак у t нужно брать противоположным знаку с.

Множитель взятый со знаком, противоположным знаку слагаемого с, называется нормирующим множителем.

Введем теперь фундаментальное понятие тклонения произвольной точки М от прямой L. Пусть число d означает расстояние от точки М до прямой L. Назовем отклонением  точки М от прямой L число +d, если точка М и начало координат О лежат по разные стороны от прямой L, и число –d в случае, когда М и О лежат по одну сторону от L.

Если же начало координат лежит на прямой L, то отклонение +d положим, когда М лежит по ту сторону от L, куда направлен нормальный вектор n , и –d в противном случае.

Запишем без доказательства, что левая часть нормированного уравнения прямой равна отклонению точки М с координатами (x,y) от прямой, определяемой этим нормированным уравнением. Это дает возможность легко определить расстояние от точки до прямой. Для этого достаточно нормировать уравнение прямой и подставить в него координаты точки (x,y):