Поверхности второго порядка.

Поверхностью второго порядка будем называть геометрическое место точек в пространстве, удовлетворяющих уравнению:

где по крайней мере один из a₁₁ a₂₂ a₃₃  0. Это уравнение называется общим уравнением поверхности второго порядка.

Назовем группу слагаемых группой старших членов, а - линейной частью. a₄₄ – свободный член.

Перейдем к новой системе координат с целью упростить общее уравнение.

Сначала осуществим параллельный перенос:

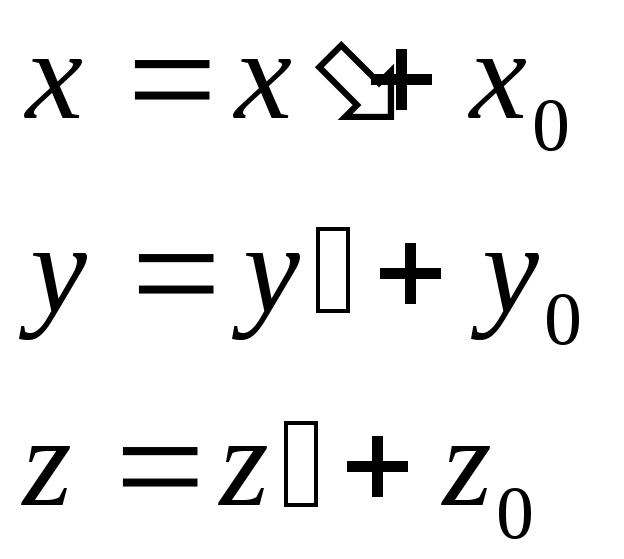
Подставив в общее уравнение, получим:

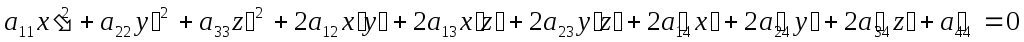где (*)

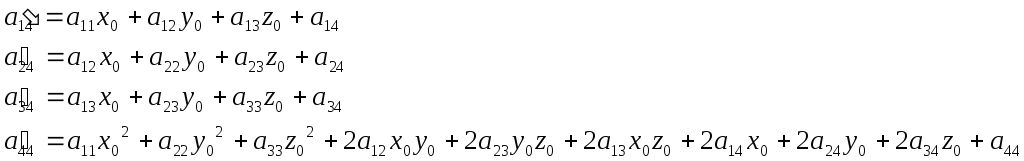Важный вывод: при параллельном переносе системы координат коэффициенты при старших членах не изменяются! Преобразуются коэффициенты группы линейных членов по некоторым формулам.

Рассмотрим поворот осей:

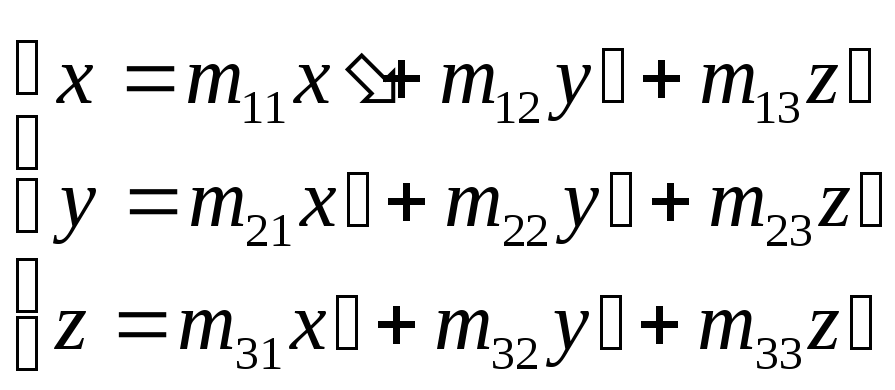
Если введем эти координаты в общее уравнение поверхности, сгруппируем члены при различных степенях x’ y’ z’ и получим:

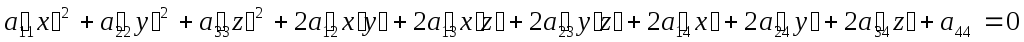
Легко убедиться, если расписать коэффициенты и т.д., что: при повороте сисемы координат коэффициенты старших членов зависят лишь от m_ij и старых коэффициентов старших членов, а коэффициенты - зависят только от m_ij и , а не изменяется! При этом, если в исходном уравнении коэффициенты были равны нулю, то и будут равны нулю! Другими словами, при параллельном переносе можно упрощать группу линейных членов, а при повороте – упрощать группу старших членов уравнения.

Оказывается, существуют инварианты относительно любого преобразования системы. Это величины:

Центр поверхности второго порядка.

Поставим задачу найти такую систему координат, в которой уравнеие поверхности не содержало бы линейных слагаемых, т.е. . Пусть точка O(x₀ y₀ z₀) это точка начала координат искомой системы. Тогда, вспоминая формулы для параллельного переноса системы координат (*), имеем:

(**)

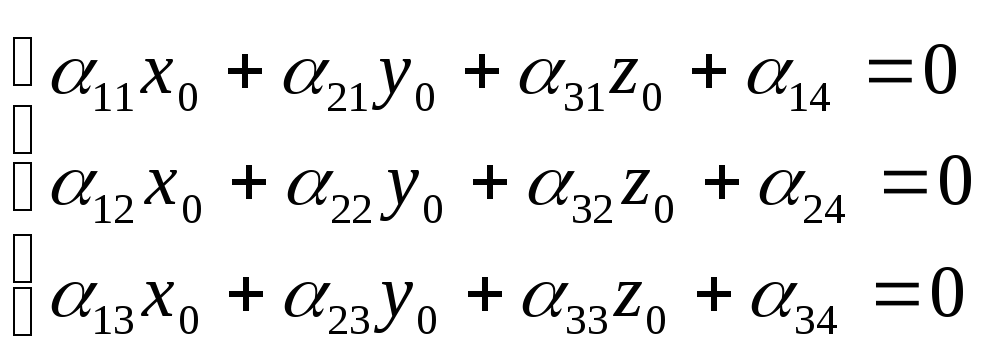Эти уравнения называются уравнениями центра поверхности второго порядка. Если координаты центра найдены, то осуществляя параллельный перенос начала координат в центр, получим уравнение поверхности:

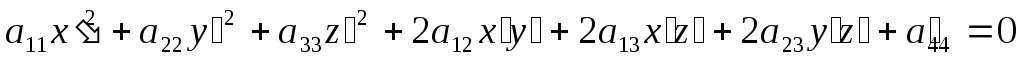
Ну и наконец, запишем без доказательства, что всегда существует некоторая декартова система координат, в которой последнее уравнение не содержит членов с x’y’ ; x’z’ ; z’y’. К этой системе можно прийти путем поворота осей координат координатной системы. В этой системе координат уравнение поверхности примет вид:

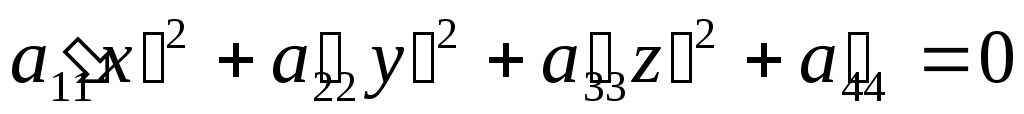
Процедура параллельного переноса и последующего поворота системы координат с целью получения этого уравнения называется стандартным упрощением уравнения поверхности.

Заметим, что не всякая поверхность может быть центральной, а лишь та, где I₃  0.

Действительно, I₃ является определителем системы уравнений (**) и для существования единственного решения этой системы по теореме Кронеккера-Капелли I₃ не должен быть равен нулю. Если же I₃ = 0, то у поверхности нет центральной точки. Ее уравнение может быть сведено к виду

Такая поверхность называется нецентральной.

Лекция 10. Классификация поверхностей 2го порядка

Итак, путем стандартного упрощения уравнения поверхности, уравнение может принять вид:

a₁₁ x² + a₂₂ y² + a₃₃ z² + a₄₄ = 0

Это уравнение есть уравнение только центральной поверхности! Тогда, поскольку I₃  0, то I₃ = a_11* a_22* a₃₃  0 означает, что a₁₁  0, a₂₂  0, a₃₃  0.

Возможны следующие случаи:

1). a₁₁ a₂₂ a₃₃ одного знака. а₄₄  0. Поверхность S называется эллипсоидом. Причем мы будем рассматривать только случай, когда знак у a₁₁ a₂₂ a₃₃ и у а₄₄ противоположный – вещественный эллипсоид. Каноничаская форма уравнения эллипсоида:

2). Два коэффициента одного знака, два противоположного:

- это уравнение однополостного гиперболоида.

3). Наконец, знак у а₁₁, а₂₂ и а₄₄ противоположен знаку у а₃₃

- уравнение двухполостного гиперболоида.

4). Левая часть равна нулю. Очевидно, для вещественного конуса необходимо, чтобы знак при a₁₁ a₂₂ или a₃₃ был противоположен двум другим

- вещественный конус второго порядка.

Оси OX OY OZ – центральные оси этих четырех поверхностей.