
- •Курс лекций по линейной алгебре и аналитической геометрии
- •Обратная матрица
- •Лекция 3.
- •Понятие вектора
- •Скалярное произведение двух векторов
- •Уравнение линии на плоскости
- •Параметрическое представление линии
- •Полярная система координат
- •Уравнение прямой в отрезках
- •Каноническое уравнение прямой
- •Параметрическое уравнение прямой
- •Прямая с угловым коэффициентом
- •Угол между двумя прямыми
- •Нормированное уравнение прямой
- •Уравнение прямой линии в полярных координатах
- •Лекция 7. Линии второго порядка
- •Лекция 8. Плоскость. Различные ее виды
- •Уравнение плоскости, проходящей через три заданные точки
- •Лекция 9. Преобразование декартовых прямоугольных координат на плоскости и в пространстве
- •Заметим, что
- •Поверхности второго порядка.
- •Центр поверхности второго порядка.
- •Лекция 10. Классификация поверхностей 2го порядка
- •Нецентральные поверхности второго порядка. Очевидно, нецентральная поверхность имеет уравнение:
- •Лекция 11. Линейные пространства
- •Некоторые свойства произвольных линейных пространств.
- •Размерность и базис линейного пространства.
- •Действия над векторами в координатной форме.
- •Замена базиса
- •Лекция 12. Евклидовы пространства.
- •Неравенство Коши-Буняковского
- •Норма вектора. Нормированное пространство
- •Ортонормированный базис конечномерного Евклидового пространства
- •Ортогональные матрицы и их свойства
- •Лекция 13. Линейные операторы.
- •Действия над линейными операторами
- •Матрица линейного оператора.
- •Изменение матрицы линейного оператора
- •Собственные числа и собственные векторы
- •Линейные операторы в евклидовом пространстве
- •Рассмотрим некоторые примеры линейных операторов
- •Квадратичные формы и их приведение к каноническому виду
Скалярное произведение двух векторов
Определение 1.
Скалярным произведением двух векторов называется число, равное произведению длин этих векторов на косинус угла между ними.
Будем обозначать
символами
![]()
![]()
Вспомним определение проекции вектора на ось:
проекция![]() или проекция
или проекция![]()
Т.е. другое определение скалярного произведения:
![]()
Понятие скалярного произведения родилось в механике. Оно означает работу силы, равной вектору a на перемещении, равном вектору b.
Два вектора называются ортогональными, если угол между ними равен 90о.
Теорема. Необходимым и достаточным условием ортогональности двух векторов является равенство нулю их скалярного произведения.
Необходимость:
пусть
![]() и
и![]() ортогональны. Т.е.
ортогональны. Т.е.![]() .
.
Достаточность:
пусть
![]() .
Если
.
Если![]() ,
то остаётся
,
то остаётся![]() т.е.
т.е.![]() .
.
Алгебраические свойства скалярного произведения:
1).
![]() переместительное свойство.
переместительное свойство.
2).
![]() сочетательное относительно числового
множителя.
сочетательное относительно числового
множителя.
3).
![]() распределительное относительно суммы
векторов.
распределительное относительно суммы
векторов.
4).
![]() если
если![]() и
и![]() , если
, если![]() .
.
Докажем, допустим,
свойство 2:
![]() .
.
Эти четыре свойства позволяют при скалярном перемножении векторных многочленов выполнить действия почленно, не заботясь о порядке и сочетая числовые множители. Используем эти свойства практически. Найдём выражение скалярного произведения в декартовых координатах.
Если два вектора
![]() ,
то их скалярное произведение есть
,
то их скалярное произведение есть
![]() .
.
Для доказательства составим скалярные произведения:

и запишем:
![]() .
.
Следствие 1.
Необходимое и достаточное условие
ортогональности двух векторов является
равенство
![]() .
.
Следствие 2. Угол между двумя векторами есть:
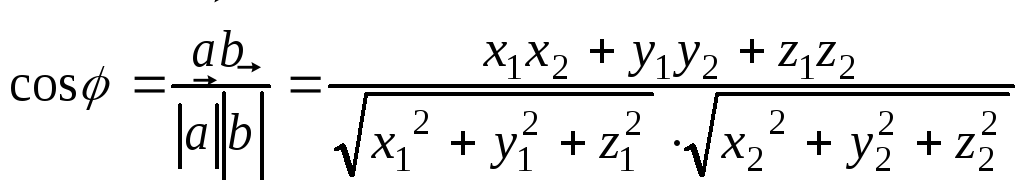 .
.
Векторное и смешанное произведения векторов
Прежде всего
назовём три вектора упорядоченной
тройкой, если указано, какой вектор
называется первый, второй и третий. Так,
запись
![]() означает,
что
означает,
что![]()
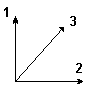 - правая
тройка
- правая
тройка
Определим правую систему координат по правилу правой руки или по правилу буравчика.
Определение: аффинная система координат называется правой, если три базисных вектора образуют правую систему координат.
Определение
векторного произведения:
векторным произведением вектора
![]() на
вектор
на
вектор![]() называется
вектор
называется
вектор![]() ,
обозначаемый
,
обозначаемый![]() и
удовлетворяющий требованиям:
и
удовлетворяющий требованиям:
длина вектора
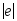 равна:
равна: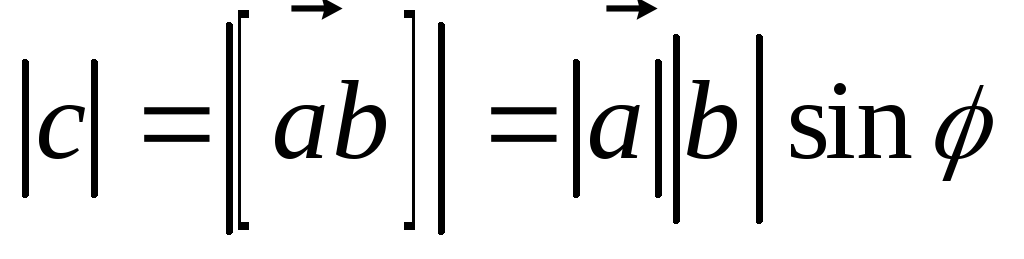 ;
;вектор
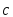 ортогонален
каждому из
ортогонален
каждому из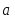 и
и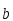 ;
;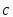 направлен
так, что
направлен
так, что
 -правая
тройка.
-правая
тройка.
Понятие векторного произведения родилось тоже в механике.
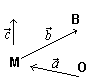
![]() -момент
М
силы
-момент
М
силы
![]() относительно
точки О.
относительно
точки О.
Теорема. Необходимым и достаточным условием коллинеарности двух векторов является равенство нулю их векторного произведения.
Необходимость вытекает из самого определения векторного произведения.
Достаточность.
Пусть
![]() .
Тогда
.
Тогда![]() и
и![]() ,
и остаётся
,
и остаётся![]() ,
т.е. коллинеарность
,
т.е. коллинеарность
Теорема.
Модуль векторного произведения равен
площади параллелограмма, построенного
на приведённых к общему началу векторах
![]() .
Эта теорема непосредственно вытекает
из формулы
.
Эта теорема непосредственно вытекает
из формулы![]() .
.
Смешанное произведение трёх векторов
Если вектор![]() векторно умножается на вектор
векторно умножается на вектор![]() ,
затем получившийся вектор
,
затем получившийся вектор![]() скалярно умножается на вектор
скалярно умножается на вектор![]() ,
то в результате получается число
,
то в результате получается число![]() ,
называемое смешанным произведением
векторов
,
называемое смешанным произведением
векторов![]() .
.
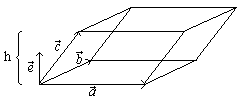
Теорема.
Смешанное произведение
![]() равно объёму параллелепипеда, построенного
на векторах
равно объёму параллелепипеда, построенного
на векторах![]() и
взятому со знаком плюс, если тройка
и
взятому со знаком плюс, если тройка![]() -
правая, и минус если тройка левая. Докажем
для правой тройки:
-
правая, и минус если тройка левая. Докажем
для правой тройки:
![]()
Следствие 1:
Справедливо равенство:
![]() .
Доказанное равенство позволяет записывать
смешанное произведение, не указывая
при этом, какое произведение векторное,
какое скалярное. Обозначается смешанное
произведение
.
Доказанное равенство позволяет записывать
смешанное произведение, не указывая
при этом, какое произведение векторное,
какое скалярное. Обозначается смешанное
произведение![]() .
.
Следствие 2: Необходимым и достаточным условием компланарности трех векторов является равенство нулю их смешанного произведения.
Следствие 3: Смешанное произведение трёх векторов, два из которых совпадают, равно нулю. В самом деле, такие векторы колмпланарны заведомо.
Алгебраические свойства векторного произведения
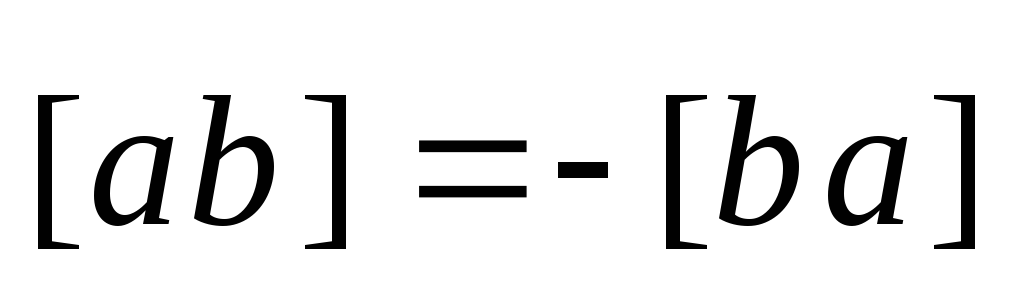 - антиперестановочность
сомножителей.
- антиперестановочность
сомножителей.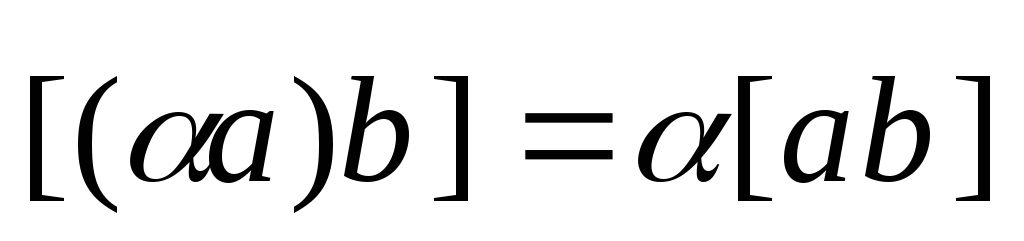 - сочетательное
относительно числового множителя.
- сочетательное
относительно числового множителя.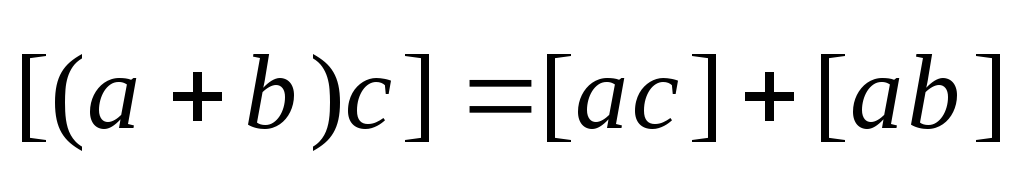 - распределительное
относительно суммы векторов.
- распределительное
относительно суммы векторов.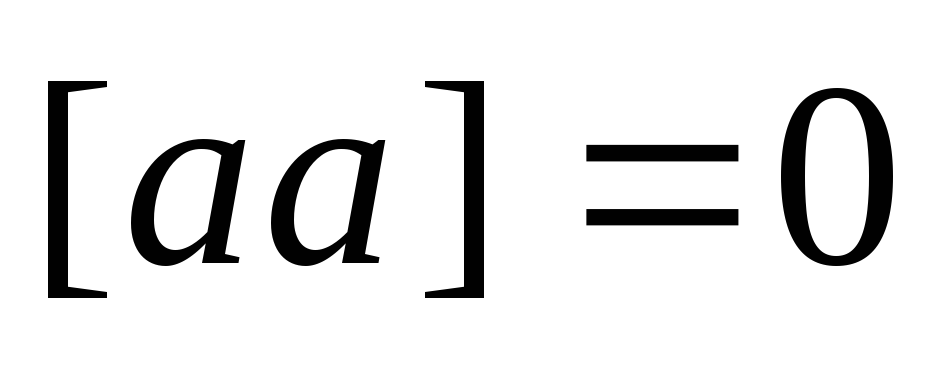 для любого
для любого
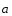 .
.
Для доказательства
свойства 1 (ограничимся доказательством
только первого свойства) вспомним о
правой и левой тройках векторов. Если
считать, что
![]() образуют
правую тройку, то
образуют
правую тройку, то![]() очевидно левая тройка. Значит по
определению векторного произведения,
векторы
очевидно левая тройка. Значит по
определению векторного произведения,
векторы![]() коллинеарны, одинаковой длины и
противоположно направлены, т.е.
коллинеарны, одинаковой длины и
противоположно направлены, т.е.![]() ,
что и доказывает первое свойство.
,
что и доказывает первое свойство.
Эти четыре свойства позволяют оперировать при векторном перемножении сомножителями почленно, производить сочетание множителей, не меняя при этом порядок векторного умножения.
Выражение векторного произведения в декартовых координатах
Если два вектора
имеют координаты
![]() ,
то их векторное произведение можно
найти, опираясь на свойства векторного
произведения:
,
то их векторное произведение можно
найти, опираясь на свойства векторного
произведения:
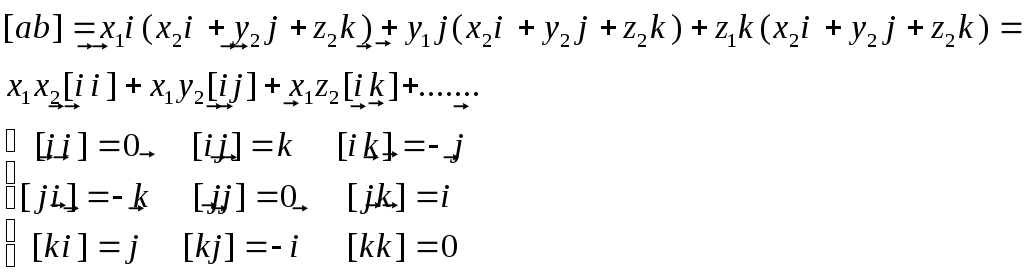
В итоге
![]() (*)
(*)
или
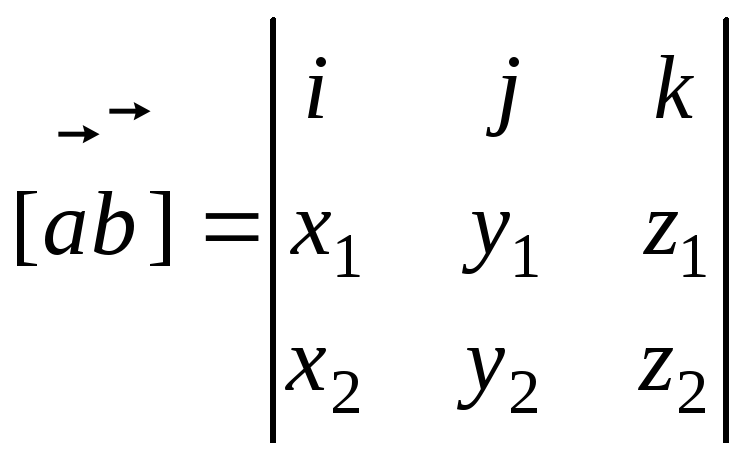 -
разложение определителя по первой
строке.
-
разложение определителя по первой
строке.
Следствие.
Если два вектора
![]() коллинеарны,
то координаты их пропорциональны.
Действительно, векторное произведение
коллинеарных векторов равно нулю. Но
из равенства (*) следует (поскольку
коллинеарны,
то координаты их пропорциональны.
Действительно, векторное произведение
коллинеарных векторов равно нулю. Но
из равенства (*) следует (поскольку![]() ):
):![]() .
.
Выражение смешанного произведения в декартовых координатах
Смешанное
произведение трёх векторов
![]() равняется определителю, строки которого
составлены из координат соответствующих
векторов.
равняется определителю, строки которого
составлены из координат соответствующих
векторов.

Действительно,
координаты
![]() определяются выражением:
определяются выражением:
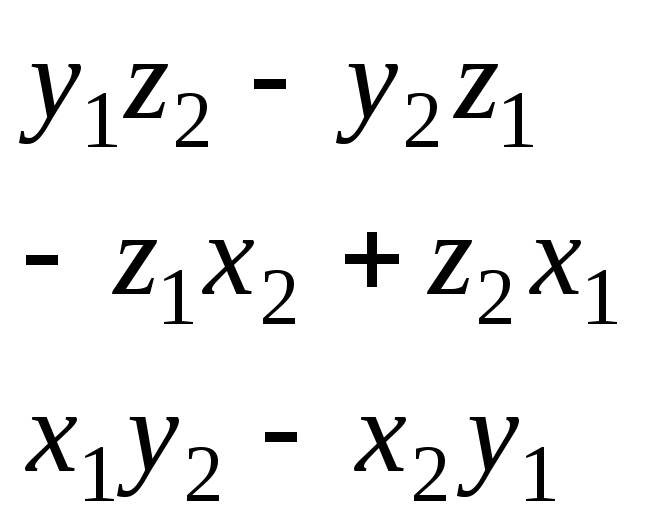
а координаты
скалярного произведения, вспомним, есть
![]() ,
или, в нашем случае,:
,
или, в нашем случае,: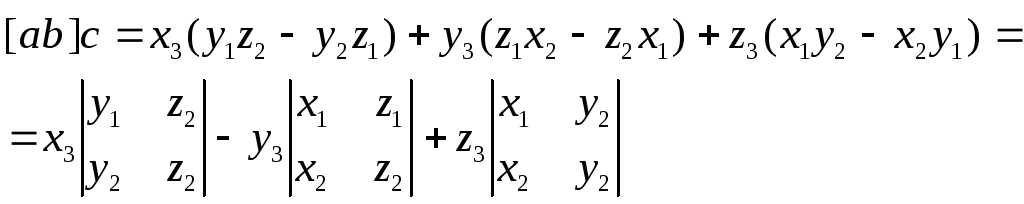
А это разложение определителя по третьей строке.
Следствие:
необходимым и достаточным условием
коллинеарности трёх векторов с
координатами
![]() является равенство нулю определителя
является равенство нулю определителя
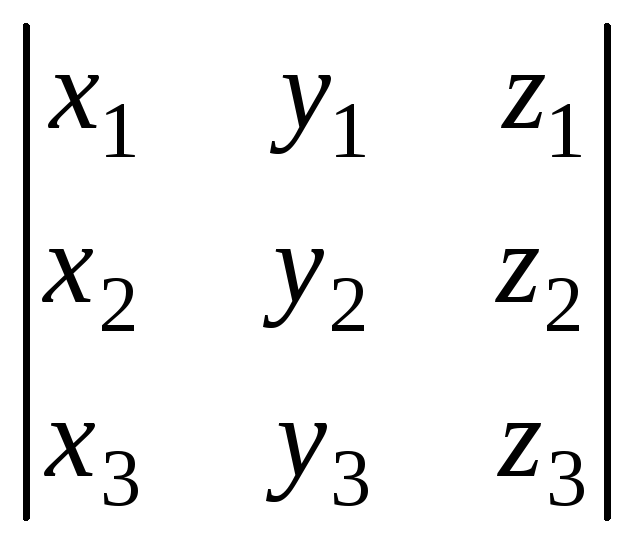 .
.
Лекция 6.
Аналитическая геометрия
