
- •1. Векторы и действия над ними. Свойства операций над векторами. Векторная запись системы линейных уравнений.
- •Свойства операций над векторами:
- •3. Понятие ранга и базиса системы векторов. Алгоритм нахождения ранга системы векторов.
- •7. Понятие обратной матрицы, необходимые и достаточные условия ее существования. Утверждения, связанные с необходимыми условиями существования обратной матрицы.
- •8. Теорема существования обратной матрицы. Вычисление обратной матрицы. Решение систем линейных уравнений и матричных уравнений с использованием обратной матрицы.
- •9. Понятие ранга матрицы. Теорема о ранге матрицы. Нахождение ранга матрицы.
- •10. Определение ранга ч-з минор. Метод окаймляющих миноров.
- •11. Формулы Крамера для решения системы п уравнений с п неизвестными. Условия, при которых применимы формулы Крамера.
- •12. Теорема Кронекера-Капелли.
- •13. Теорема о множестве решений однородной системы, определитель которой равен нулю.
- •16. Собственные векторы и собственные значения матриц. Характеристический многочлен и характеристическое уравнение матрицы а.
- •17. Модель международной торговли (линейная модель обмена). Условия сбалансированности.
- •18. Межотраслевая модель экономики (модель Леонтьева)
Вопросы к экзамену.
1. Векторы и действия над ними. Свойства операций над векторами. Векторная запись системы линейных уравнений.
Упорядоченный
набор n
действительных чисел
 будем называть n-
мерным вектором,
его элементы
будем называть n-
мерным вектором,
его элементы
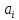 (i
= 1, 2, …, n)
назовем компонентом вектора, n
– размерность вектора
(i
= 1, 2, …, n)
назовем компонентом вектора, n
– размерность вектора
Операции над векторами:
Равенство В.
Будем
говорить, что 2 вектора
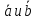 равны
между собой
равны
между собой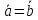 ,
если они имеют одинаковую размерностьn
и их соответствующие компоненты равны,
т.е
,
если они имеют одинаковую размерностьn
и их соответствующие компоненты равны,
т.е
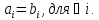
Умножение вектора на число.
Произведение
вектора на число - это вектор
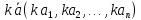 .
.
Сумма векторов.
Суммой
векторов
 ,
имеющих одинаковую размерность, является
вектор:
,
имеющих одинаковую размерность, является
вектор:
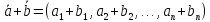
Скалярное произведение векторов.
Скалярное
произведение 2-х векторов
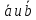 ,
имеющих одинаковую размерность,
определяется как сумма произведений
соответствующих компонент. Обозначается
: (
,
имеющих одинаковую размерность,
определяется как сумма произведений
соответствующих компонент. Обозначается
: (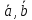 )
)
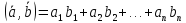
Свойства операций над векторами:
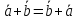
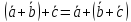
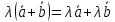
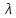 –действительное
число.
–действительное
число.(
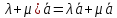
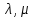 – действительные числа.
– действительные числа.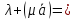 (
(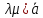

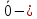 вектор,
все компоненты к-го раны нулю.
вектор,
все компоненты к-го раны нулю.
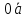 =
=

(
 )
= (
)
= (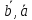 )
) (
(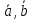 )
=
)
=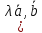 )
= (
)
= (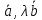 )
)
Назовем
любое мн-во векторов
 системой
векторов,
если они имеют одинаковую размерность,
обозначать будем:
системой
векторов,
если они имеют одинаковую размерность,
обозначать будем:
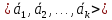
Будем
говорить, что вектор
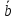 является линейной комбинацией векторов
является линейной комбинацией векторов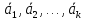 ,
если
,
если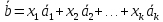 .
Здесь
.
Здесь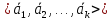 система векторов одинаковой размерности,
а коэф-ты
система векторов одинаковой размерности,
а коэф-ты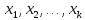 – действительные числа. Или будем
говорить, что вектор
– действительные числа. Или будем
говорить, что вектор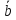 линейно выражается ч-з вектора
линейно выражается ч-з вектора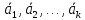 .
Набор
.
Набор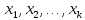 называется тривиальным, если все они
раны нулю, т.е.
называется тривиальным, если все они
раны нулю, т.е.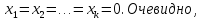 что
в данном случае линейная комбинация
любых векторов
что
в данном случае линейная комбинация
любых векторов обращается в нуль.
обращается в нуль.
Векторная запись систем линейных уравнений.
Введем
обозначения:
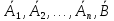 – это вектора-столбцы, причем:
– это вектора-столбцы, причем:
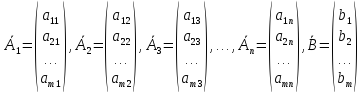
Как
можно интерпретировать запись:
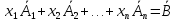 (*)?
(*)?
Запись (*) соответствует системе уравнений, в к-ой n ур-й и n неизвестных.
2. Линейная комбинация векторов. Понятие линейной зависимости и независимости системы векторов. Утверждения, связанные с линейной зависимостью (независимостью) векторов.
Будем
говорить, что вектор
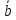 является линейной комбинацией векторов
является линейной комбинацией векторов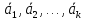 ,
если
,
если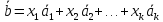 .(*)
Здесь
.(*)
Здесь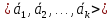 система векторов одинаковой размерности,
а коэф-ты
система векторов одинаковой размерности,
а коэф-ты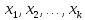 – действительные числа. Или будем
говорить, что вектор
– действительные числа. Или будем
говорить, что вектор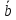 линейно выражается ч-з вектора
линейно выражается ч-з вектора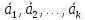 .3.
Утверждения,
связанные с линейной зависимостью
(независимостью) векторов.
.3.
Утверждения,
связанные с линейной зависимостью
(независимостью) векторов.
Одинаковой размерности
Тривиальны
Система
векторов
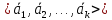 называется
линейно независимой, если равенство
(*) = 0 выполняется, только при тривиальном
наборе коэф-в.
называется
линейно независимой, если равенство
(*) = 0 выполняется, только при тривиальном
наборе коэф-в.
 )
)
Система
векторов линейно
зависимой в противном случае, т.е если
рав-во (*)=0 выполняется, когда хотя бы 1
из коэф-в
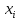 (i
=1, 2…k)
отличен от нуля.
(i
=1, 2…k)
отличен от нуля.
Утверждения, связанные с линейной зависимостью (независимостью) векторов.
1. Если в системе векторов есть нулевой вектор, то она линейно зависима.
2. Если векторы а1,а2,а3,...,ак линейно независимы, а векторы а1,а2,а3,...,ак,b линейно зависимы, то вектор b линейно выражается через векторы а1,а2,а3у...,ак.
3.
Пусть в системе <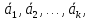 >(1**)
>(1**)
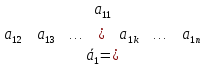
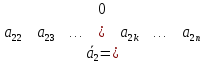
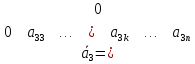
……………………………………..
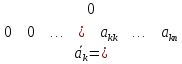
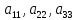 ,
,
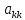 ≠0.Тогда
данная система векторов линейно
независима.
≠0.Тогда
данная система векторов линейно
независима.
4.
Если система векторов <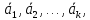 линейно
зависима, то некоторый вектор этой
системы линейно выражается через другие.
линейно
зависима, то некоторый вектор этой
системы линейно выражается через другие.
5.
Если к системе линейно зависимых векторов
<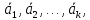 >добавить
произвольный вектор Ь,
то
система
>добавить
произвольный вектор Ь,
то
система
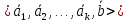 останется
линейно зависимой.
останется
линейно зависимой.
6. Удаление одного вектора из системы линейно независимых векторов оставляет систему линейно независимой.
7. Прибавление к одному вектору линейно независимой системы другого вектора этой системы, умноженного на какое-либо действительное число, оставляет систему линейно независимой.
8. Умножение одного из векторов линейно независимой системы на число, отличное от нуля, оставляет систему линейно независимой.
9. Прибавление к одному вектору линейно зависимой системы другого вектора этой системы, умноженного на какое-либо действительное число, оставляет систему линейно зависимой.
10. Умножение одного из векторов линейно зависимой системы на число, отличное от нуля, оставляет систему линейно зависимой
Замечание. Последние четыре утверждения можно обобщенно сформулировать так:
Гауссовские преобразования не изменяют линейной зависимости или независимости системы векторов.
