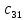16. Собственные векторы и собственные значения матриц. Характеристический многочлен и характеристическое уравнение матрицы а.

Рассмотрим квадратную матрицу А (n*n). Рассмотрим мн-во векторов –столбцов размерности n. В рез-те произведение это матрицы на n-мерный вектор х получиться также n-мерный вектор у: АХ=У

Число α наз-ся собственным значением кв матрицы А, если найдется вектор х, такой, что ах= λ х

Пример

Собственное значение λ = 5. Собственный вектор (1,1).

Каждый вектор где с – произвольное число, является собственным вектором матрицы А.

Рассмотрим для удобства кв матрицу А(2*2) и равно ах=х. Или Ах=λех

Ах- λех=0

0 –нулевая матрица – вектор.

(А- λе) х = 0

Матричному уравнению соответствует однородное уравнение квадратной матрицей (А-λЕ). По теореме ненулевое решение однородной системы существует такая и только такая, когда определитель системы равен 0.

= 0

Теорема. Собственным значением матрицы является решение ур-я . Это ур-е являетсяхарактеристическим уравнением матрицы А. Это многочлен степени n относительно неизвестной λ.

Собственный вектор при любом с ≠0, образует базис пространства R²

Пример.

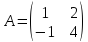
- характеристический многочлен.

λ=2 λ=3

Матрица имеет 2 собственных значения. Найдем собственные вектора.

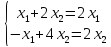
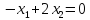
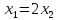
Общее решение:

(2с, с), где с – любое действительное число. То же самое, если λ=3

Замечание:

Собственные векторы, при любом с≠0, образуют базис пространства R².

17. Модель международной торговли (линейная модель обмена). Условия сбалансированности.

Предположим, что n стран или к-либо других автономных сообществ людей осуществляют между собой торговлю. Пусть доход i-ой страны от торговли составляет х ден. ед. - доля дохода, которуюj-ая страна тратит на закупку товара у i-ой страны. S - НД

A =

Расходы

В экономической лит-ре наз-ся структурной матрицей торговли. Ограничимся ситуацией, когда страна тратит все на покупку собственных товаров и товаров из других стран. Тогда (сумма по столбцу)

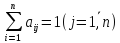
Произведение представляет собой выручку i-ой страны от продажи товаров j-ой. Поэтому суммарная выручка i-ой страны от продажи товаров на внутреннем и внешнем рынке:

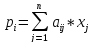
Сбалансированная торговля – НД и выручка равны м-у собой.

В матричном виде: Х(х₁, х₂,…, х_n)^т – вектор доходов.

X=AX

AX=P

18. Межотраслевая модель экономики (модель Леонтьева)

Модель предполагает, что экономика состоит из некоторого числа взаимодействующих отраслей, каждая из которых воображаемо производит только один вид продукции и использует только 1 процесс производства.

Предположим, что имеется n отраслей. Каждая производит продукции в точности столько, сколько требуется для удовлетворения потребностей других отраслей и рынка.

– кол-во единиц продукции, произведенной i-ой отраслью в данном году.

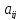- кол-во продукции i-ой отрасли, необходимой для произ-ва 1 ед продукции j-ой отрасли при неизменной технологии. Этот коэффициент пропорционально зависит от технологии j-ой отрасли и наз-ся коэффициентом прямых затрат. И сама i-ая отрасль также использует часть своей продукции на пр-во. Величина идущая на потребление, др словами на свободный рынок, наз-сяпродуктом конечного потребления.

i-ая отрасль вырабатывает продукции:

Например, имеются 3 отрасли;

Объем продукции (валовой выпуск?)

В балансовой модели Леонтьева объем продукции х складывается из продукции АХ, идущей на пр-во и потребление. Определим У:

Тогда: Х=АХ+У (*)

Уравнение (*) наз-ют уравнением линейного межотраслевого баланса. Оно используется двояко.

В 1 случае известен валовой продукт и нужно рас-ть вектор конечного потребления.

Во 2 случае уравнение межотраслевого баланса используется с целью планирования. Здесь на определенном промежутке времени известен вектор конечного потребления и требуется найти вектор валового выпуска продукции.

Т.о. в 1 случае:

(ЕХ-АХ)=У (Е-А)*Х=У

В случае невыраженности матрицы (Е-А) получим: Х = (Е-А)^-1 * У

И во 2 случае: Х = (Е-А)^-1 * У

Пример.

Данные о работе 2-х фирм приведены в таблице.

Фирма	Поставки фирме
	1-й	2-й
1	0,1	0,4
2	0,8	0,2

Пусть ВВ продукции . Найдем вектор конечного потребления.

Решение.

Составим матрицы задачи Леонтьева.

Подставим данные в ур-е и получаем:

У= (Е-А)*Х=

Пример 2. -//-

Пусть задан вектор конечного потребления.. Требуется найти ВВ продукции Х.

Найдем обратную матрицу:

(Е-А)^-1 =

Х = (Е-А)^-1 * У = =

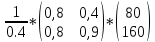19. Построение экономико-математических моделей и задача линейного программирования. Задача об использовании ресурсов, задача о диете, транспортная задача. Графический метод решения задачи линейного программирования с 2 переменными.

Задача линейного программирования состоит в нахождении такого решения системы линейных ограничений, для которого ф-я, рассматриваемая на мн-ве всех решений, достигает своего наибольшего, либо наименьшего значения. Другими словами, в определении такого решения системы линейных уравнений или неравенств вида:

которые давали бы максимальную (миним) величину линейной ф-ции

Задача об использовании ресурсов. Предприятие имеет 2 вида ресурсов. В нашем случае - R₁ и R₂. В кол-ве b₁ и b₂. Изготавливаются 2 вида продукции T₁ и T₂. а_ij – расход i –го сырья на j-ый вид продукции. Эта инфо задается матрицей А.

Общий вид задачи:

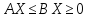
Задача о диете

Для животноводческого комплекса необходимо составить такой рацион, который удовлетворял бы суточным потребностям животных в тех или иных питательных веществах, был бы по возможности дешев и состоял из имеющихся в распоряжении продуктов.

– сколько в-ва находиться в продукте

A(4*3)

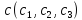
Введем величины .

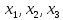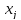– кол-во продукта , которое будет употреблено для смеси.

СХ – суточная стоимость рациона

Составим суточный рацион, который удовлетворял бы потребностям и был минимальным по стоимости.

Транспортная задача

Пусть необходимо перевезти однородный груз из пунктов его пр-ва или хранения в пункты его потребления. При этом ставиться задача свести к минимуму транспортные расходы.

Пусть есть пункты поставки

И там находиться ед груза:

Пункты потребления

Их потребности составляют:

стоимость перевозки ед товара из пункта в

План перевозок можно задать в таблице:

- кол-во груза, которое нужно перевезти из пункта в

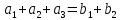Если выполняется условие: . То задача наз-ся сбалансированной. Поэтому:

Стоимость перевозки из i-го пункта в j-ый равна

Т.о.: 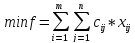на мн-ве решений системы ограничений (*).

В общем случае, мн-во допустимых решений представляет собой пересечение полуплоскостей. Такое мн-во является выпуклым.

1. В случае если эта область является многоугольником (ограничено), то оптимальное решение всегда сущ-ет. Максимальное (минимальное) значение ф-ции достигается в какой-либо вершине этого многоугольника, т.е достаточно определить вершины многоугольника и выделить ту из них, для которой значение ф-ции является наибольшим (либо наименьшим).

2. Если мн-во допустимых решений не содержит ни одной точки, то задача не имеет решений.

3. Если образует неограниченную многоугольную область то

   1. решение находиться в какой-либо вершине области решений

   2. заданная ф-ция не ограничена сверху (снизу). Можно выяснить по расположению линий уровня в конкретном случае при изменении значений ф-ций.