3. Понятие ранга и базиса системы векторов. Алгоритм нахождения ранга системы векторов.

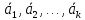Рангом системы векторов <> называется наибольшее число линейно независимых векторов.

Базисом системы векторов является наибольшее подмножество линейно независимых векторов.

Алгоритм:

Выпишем координаты векторов в виде таблицы:

Будем преобразовывать с помощью преобразование 1 и 2 вида, стремясь получить нули левее и ниже диагонали. Эти преобразования изменяют вектора, входящие в систему, но система сохраняет свою линейную зависимость или независимость. Появившиеся 0 строки – вычеркиваем. Преобразования закончена если таблица коэф-в имеет трапециевидный, треугольный или ступенчатый вид. Число оставшихся ненулевых строк и является рангом системы векторов. Если мы каждый раз прибавляем строки с меньшим номером к строкам с большим номером, то обнулившиеся строки линейно зависят от предыдущих, а те вектора, что были записаны в ненулевых строках первоначально, образуют базис.

Ступенчатый вид таблицы – таблица, в которой каждая следующая строка начинается с большего числа нулей, чем предыдущая.

4. Матрицы и действия над ними. Свойства операций над матрицами. Запись системы линейных уравнений в виде матричного равенства.

Матрицы и действия над ними.

Прямоугольную таблицу вещественных чисел будем называть матрицей. Обозначать - А, В, С…:

m – число строк; n – число столбцов.

Эти числа определяют размерность матрицы – (mn)

Элемент стоит вi-ой строке и j-ом столбце.

Среди матриц выделяют квадратные матрицы. В этом случае m=n. Иногда говорят, матрица n-го порядка, что означает квадратную матрицу, у к-ой число строк = числу столбцов.

Иногда матрицу с одной строкой А(1n) удобно рассматривать как вектор, называя её вектором-строкой или матрицей-строкой.

Матрицу с одним столбцом А(m1) можно рассматривать как вектор, называя её вектором-столбцом или матрицей-столбцом.

Операции над матрицами.

Равенство матриц.

Матрица А равна матрице В, если их размерности одинаковы и эл-ты, стоящие на одинаковых местах равны между собой, т.е.

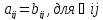
Сумма матриц.

Суммой 2-х матриц А и В, имеющих одинаковую размерность (mn) называют матрицу С, С=А+В, эл-ты матрицы С получаются сложением элементов, стоящих на одинаковых местах, т.е.

Умножение М на число.

Умножение М на число означает умножить каждый элемент М на это число, т.е. результатом произведения матрицы А на действительное число λ является матрица С, элементы к-ой определяются по правилу:

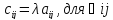
Произведение матриц.

Произведение М определяется не для всех М. Накладываются условия: A(mn) и B (nr).

Пусть заданы 2 матрицы: A(23) иB (32).

Результатом произведения является М С=АВ размерности (mr), эл-ты к-ой вычисляются по формуле:

C = (,)

Матричная запись систем уравнений

В этой системе m- уравнений и n-неизвестных. – или переменные, числа – к-т привi-ом уравнении, 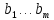- свободные члены.

Рассмотрим матрицу системы:

5. Вычисление определителей 2-го и 3-го порядков. Определитель n-го порядка для квадратной матрицы. Свойства определителя.

Каждая квадратная М имеет определитель.

Определитель n-го порядка.

Назовем определителем сумму вида:

- элемент i-ой строки.

–определитель, полученный вычеркиванием i-ой строки и каждого столбца.

Замечание: Выбор сроки не влияет на значение определителя.

Это индуктивное определение.

Свойства:

1.

2. Если 2 строки (столбца) равны между собой, то def М = 0

3.def, содержащий нулевую строку (столбец) =0

4. Если поменять местами 2 строки (), то знак def поменяется на противоположный.

5. Общий множитель строки () можно вынести за знак определителя.

6. Если каждый элемент некоторой строки () представлен в виде суммы 2-х слагаемых, то def может быть представлен в виде суммы 2-х определителей.

7. Определитель не измениться. Если к эл-м некоторой строки () прибавить элементы другой строки(), умноженные на одно и тоже число.

8. Сумма произведений к-либо строки () def на алгебраические дополнения, соответствующие другой строке () равна 0

9.def произведения 2-х матриц равен произведению их определителей, даже в том случае, если АВ≠ВА

6. Системы линейных уравнений. Основные понятия. Метод Гаусса. Общее и частное решение системы.

В этой системе m- уравнений и n-неизвестных. – или переменные, числа – к-т привi-ом уравнении, - свободные члены.

Опр.Решением системы (1) называется упорядоченный набор чисел (x₁⁰,x₂⁰,x₃⁰,...,x_n⁰),который при подстановке каждое уравнение системы (1) обращает в истинное равенство

Опр. Система линейных уравнений называется совместной, если она имеет хотя бы одно решение. Система линейных уравнений называется несовместной, если она не имеет ни одного решения.

1) Совместная: 3x-y=3 и –x+y=1 Решение (2,3)

2) Несовместная: x+2y=3 иx+2y=5 Не могут выполняться одновременно.

Опр.Система линейных уравнений называется определенной, если она имеет единственное решение. Если система имеет более одного решения, то она называется неопределенной.

3) Система, приведенная в 1 примере, является определенной системой.

4) Неопределенная: х+у=1 и 3х+3у=3 (0,1) (-2,3) и т.д.

Опр. Две системы линейных уравнений называются равносильными, если они имеют одно и то же множество решений

5) Имеют обе единственное решение - (2,1)

Заметим, что любые две несовместные системы с одинаковым числом переменных равносильны

Опр.Система (1), у которой все свободные члены равны нулю, называется однородной.

Очевидно, что любая однородная система совместна, т.к. в множество решений такой системы всегда входит набор (0,0,..., 0). Введем два вида гауссовских преобразований линейных систем

Преобразование 1 вида. В системе к одному из уравнений прибавляется другое уравнение системы, умноженное на какое-либо действительное число.

Преобразование II вида. В системе одно из уравнений умножается на какое-нибудь число, отличное от нуля.

Утверждение 1(2). Преобразование 1 (2) вида приводит исходную систему линейных уравнений в равносильную ей систему.

Для решения системы выпишем таблицу.

Будем применять к ней преобразования:

1. 1 и 2 вида к строкам

2. Вычеркивать 0 строки

3. Менять местами строки (столбцы)

С помощью них изменяем таблицу так, чтобы она стала треугольной (единственное решение) или трапециевидной (система неопределенна и имеет бесконечное мн-во решений).

В общем решении содержится бесконечное мн-во решений. Задавая значения свободной переменной (-ным) получаем частные решения (получая базисные)