12. Теорема Кронекера-Капелли.

Система линейных уравнений совместна тогда и только тогда, когда ранг матрицы системы равен рангу расширенной матрицы.

Ограничимся тем, что покажем: если решения есть, то ранги совпадают. Для простоты считаем, что число переменных =3.

Если () – решение, то рав-во выполняется иявляется линейной комбинацией векторовСлед-но добавление вектора в н изменяет ранга системы <>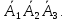

13. Теорема о множестве решений однородной системы, определитель которой равен нулю.

Т. Однородная система линейных n уравнений с n неизвестными имеет ненулевые решения тогда и только тогда, когда определитель системы равен нулю.

Утверждение1. Если определитель М равен 0, то между строками М сущ-ет линейная зависимость.

Пример def=0

Утверждение2.Пусть между строками матрицы сущ-ет линейная зависимость, тогда в произведении АВ какой бы ни была м В, сущ-ет такая же линейная зависимость, как и в матрице А.

14. Линейное пространство. Векторное пространство. Размерность и базис векторного пространства.

Мн-во, в котором определены операции сложения, * на число, удовлетвор приведенным ниже св-вам, наз-м линейным пространством, и обозначается R. Если линейное пространство из векторов то его называют векторным пространством.

Св-ва.

1. х+у=у+х

2. (x+y)+z = x+()

3. (αβ)x = α(βx) , любые действительные числа.

4. α (x+y)= αx+αy

5. (α+β)x = αx+βx

6. Существует ненулевой эл-т, такой, что : х+0=х

7. Для любого эл-та х существует противоположный эл-т (-х), такой, что: х+(-х)=0

8. 1*х=х

Размерность и базис векторного пространства.

Векторное пространство R наз-ся n- мерным, если в нем сущ-ет n линейно независимых векторов, а любые из (n+1) векторов являются линейно зависимыми. Rⁿ.

Размерность пространства – max число содержащихся в нем линейно независимых векторов.

Базис – совокупность n линейно независимых векторов n мерного пространства R.

Каждый вектор х векторного пространства Rⁿ можно представить и при том единственным образом в виде линейной комбинации векторов базиса.

15. Евклидово пространство. Длина (норма) вектора, коллинеарные векторы, угол между 2 векторами, ортогональные векторы, ортонормированный базис евклидова пространства. Теорема о наличии ортонормированного базиса в n-мерном евклидовом пространстве.

Линейное векторное пространство, в к-ом занято скалярное произведение векторов, удовлетворяющих следующим св-вам:

1.(х,у)= (у,х)

2.(х, у+z) = (x,y)+(x,z)

3.(ax, y) = a(x, y)

4.(x, x) > 0, если х – ненулевой вектор и (x, x)=0, если х – нулевой вектор.

Длиной (нормой) вектора х на евклидовом пространстве наз-ся величина (х), где

Справедливо следующее:

1.

2. где λ – действительное число

3.

4.

Угол между 2 ненулевыми n-мерными векторами a и b, явл-ся угол, косинус которого вычисляется по формуле:

Два вектора коллинеарные, если найдется такое λ, что a = λb.

Два вектора ортогональны, если их скалярное произведение равно 0.

Векторы n- мерного евклидова пространства образуют ортонормированный базис, если они попарно ортогональны и норма каждого из них = 1.

Теорема:

Во всяком n- мерном евклидовом пространстве существует ортогональный базис.

Теорема:

Каждый вектор x линейного пространства можно представить единственным способом в виде линейной комбинации вектор-базиса