7. Понятие обратной матрицы, необходимые и достаточные условия ее существования. Утверждения, связанные с необходимыми условиями существования обратной матрицы.

Назовем М В обратной к матрице А, если АВ=ВА=Е. В таком случае В = А^-1

Необходимое. Назовем квадратную м А вырожденной, если def(A)=0 и невырожденной, если def(A)≠0. Каждая невырожденная матрица имеет обратную

Утверждение 1. Если def =0. То между строками м существует линейная зависимость.

Утверждение 2. Пусть между строками м А существует линейная зависимость. Тогда в произведении АВб какой бы ни была м В, сущ-ет такая же линейная зависимость, как в исходной м А.

Утверждение 3. Вырожденная м не имеет обратной.

Достаточное. Если определитель матрицы отличен от нуля, то для нее сущ-ет обратная матрица, причем единственная.

8. Теорема существования обратной матрицы. Вычисление обратной матрицы. Решение систем линейных уравнений и матричных уравнений с использованием обратной матрицы.

Теорема: Если определитель матрицы отличен от нуля, то для нее сущ-ет обратная матрица, причем единственная.

1. Определитель.

2. Миноры

3. Транспонируем (меняем строки со столбцами)

3.

Решение (2,2)

9. Понятие ранга матрицы. Теорема о ранге матрицы. Нахождение ранга матрицы.

Рангом матрицы относительно строк (столбцов) – наибольшее число её линейно независимых векторов трок (столбцов).

Формально это 2 разных определения, но:

Теорема:

Ранг матрицы А(m*n) относительно векторов - строк равен рангу матрицы относительно векторов - столбцов.

Очевидно, что rang(A)≤min(m, n)

Для нахождения ранга М – тот же алгоритм. Но теперь будем учитывать Гауссовы преобразования, и к столбцам. При нахождении ранга можно:

1. Применить преобразования 1и 2вида к строкам и столбцам.

2. Вычеркивать 0 строки.

3. Менять местами строки.

4. -//- столбцы

Утверждение:

Преобразования 1 и 2вида не изменяют линейной зависимости или независимости векторов.

Пример. Найти РМ

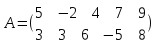
Rang(A) = 2. Строки матрицы непропорциональны, поэтому они линейно независимы.

10. Определение ранга ч-з минор. Метод окаймляющих миноров.

Рангом матрицы называется наибольший порядок минора, отличного от нуля.

Отсюда – метод окаймляющих миноров.

Утверждение:

Определитель кВ матрицы =0 в том и только том случае, если между его строками есть линейная зависимость.

Метод окаймляющих миноров.

В матрице находим элемент, не равный нулю. Если такого нет, то определитель = 0, и rang = 0. Добавляем строку к столбец к элементу, не равному 0, получаем окаймляющие миноры 2-го порядка, среди них ищем миноры, не = 0, Если такого нет, то rang=1. Если есть, то ищем окаймляющие миноры 3-го порядка и т.д. Порядок старшего минора, не =0 и есть ранг матрицы.

Пример.

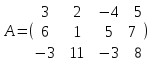
Rang(A) = 3

11. Формулы Крамера для решения системы п уравнений с п неизвестными. Условия, при которых применимы формулы Крамера.

Если в системе (1 ) m=n и def системы отличен от нуля, то такая система имеет единственное решение.

Если определитель системы (1) отличен от нуля, то система имеет единственное решение, вычисляемое по формулам Крамера:

Утверждение.

Однородная система линейных n уравнений с n неизвестными имеет ненулевые решения тогда и только тогда, когда определитель системы равен нулю.

Теорема:

Если в системе 1 число уравнений и переменных одинаково и определитель системы отличен от 0, то такая система имеет единственное решение и его можно найти по формулам Крамера.

Минор n-го порядка - это определитель матрицы А(m*n), полученный от вычеркивания некоторых строк и столбцов так, что получился минор k-го порядка.