
Lineynaya algebra i analitich_geom / Ivleva_i_kurs_lekciy_po_lineynoy_algebre_i_analiticheskoy_ge
.pdf
Курс лекций по линейной алгебре и аналитической геометрии
Рекомендуемая литература:
1.Владимир Александрович Ильин, Эдуард Генрихович Позняк Линейная алгебра, любое издание.
2.В.А.Ильин, Э.Г.Позняк
Аналитическая геометрия, любое издание. 3. Э.Л.Блох, Л.И.Лошинский, В.Я.Турин
Основы линейной алгебры и некоторые её приложения.
4.Павел Сергеевич Александров Лекции по аналитической геометрии
5.Александр Николаевич Рублев.
Курс линейной алгебры и аналитической геометрии.
6. Евгений Викторович Шикин, Алексей Викторович Боресков. Компьютерная графика. АО «ДИАЛОГ-МИФИ», 1995.
6. Давид Викторович Клетеник Сборник задач по аналитической геометрии.
Лекция 1.
Что такое алгебра ? Исторически алгебра сложилась как наука о решении уравнений. Ещё в древнем Вавилоне 4000 лет назад люди уже умели решать квадратные уравнения. Это умение возникло из практической необходимости решать задачи земледелия, строительства, военного искусства. К примеру, на одной из глиняных табличек, относящихся к тому времени учёные историки расшифровали задачу:
Площадь двух квадратов равна 1000. Сторона одного квадрата составляет две трети стороны другого, уменьшенные на 10. Каковы стороны квадратов ?
Эта задача приводит к системе уравнений:
x2 y2 1000
|
2 |
|
|
y |
x 10 |
||
3 |
|||
|
|
которая сводится к квадратному уравнению:
x2 4 x2 40 x 100 1000; 9 3
13 x2 40 x 900 0 9 3
Отсюда x=30, а y=10.
Разумеется, система записи математических соотношений была иной.
Само название “алгебра” восходит к арабским учёным. В 825 году был написан учебник “Краткая книга об исчислении ал-Джабра”. “Ал-Джабра” в переводе означает перенос или восполнение. Автор учебника – выдающийся ученый Мухаммед бен Муса аль-Хорезми. (Кстати, слово «алгоритм» произошло от латинской формы имени аль-Хорезми). Этот термин и стал названием науки. По этой книге долгое время обучалась вся Европа. Прошли столетия и в настоящее время алгебра оформилась как наука, предметом которой являются операции, записанные в символической форме. Над чем осуществлялись операции? Над математическими

моделями. Такими моделями в современной алгебре являются группы, кольца, поля, векторные пространства и т. д.
Предметом нашего изучения в курсе “линейной алгебры” являются матрицы, линейные пространства, системы линейных уравнений и др. Кроме того, мы в рамках “линейной алгебры” будем изучать геометрические объекты: вектора, уравнения линий и кривых на плоскости и в пространстве, поверхности 2-го порядка. Сам термин “линейная” означает, что над объектами изучения вводятся, т.е. определены три операции: сложение и умножение в пространстве объектов и умножение объектов на скаляр. Для определения линии в пространстве достаточно этих операций. От линии и происходит термин “линейная”.
Для чего нужен этот курс математики? Применительно к будущей специальности инженермеханик мы приведём только один пример. При создании современных машин, приборов и т.п. приходится проводить расчёты на прочность конструкций. Существует мощный современный метод - метод конечных элементов - позволяющий решать задачу расчёта на прочность сложных конструкций.
Математически этот метод сводится к решению большой системы уравнений с большим числом неизвестных. При составлении и решении этих систем уравнений интенсивно используется аппарат линейной алгебры как фундамент или основа для более сложных математических преобразований.
Одним из объектов, изучаемых в курсе линейной алгебры являются матрицы. Тема первой лекции так и называется:
Матрицы. Линейные операции над ними. Умножение матриц
Прежде чем начать изучение матриц, вспомним, что такое определитель. Рассмотрим простую задачу:
Решить систему двух уравнений с двумя неизвестными:
a x |
|
a x |
|
b |
x |
b ax |
|
|
||
|
|
1 11 1 |
|
|
||||||
|
|
|
a12 |
|
|
|||||
11 |
1 |
12 |
2 |
1 |
2 |
|
|
|
|
|
a21x1 a22x2 b2 |
|
|
|
a b aa x |
||||||
|
|
|
|
|
a x |
|
22 1 |
11 22 1 |
b |
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
21 |
1 |
|
|
2 |
|
|
|
|
|
|
|
|
|
a12 |
||
(*)
Её решение, как известно, выглядит:
x |
b1a22 a12b2 |
;___ x |
|
|
a11b2 |
a21b1 |
|||||
|
|
|
|
||||||||
1 |
a a a a |
21 |
|
2 |
|
a a a a |
21 |
||||
|
11 |
22 |
12 |
|
|
|
11 |
22 |
12 |
||
Запишем систему трёх уравнений:
a11x1 a12 x2 a13 x3 b1a21x1 a22 x2 a23 x3 b2
a31x1 a32 x2 a33 x3 b3
Запишем первые два уравнения так:
a11x1 a12x2 b1 a13x3
a21x1 a22x2 b2 a23x3
выразим неизвестную x2 из первого у-я
(**)
***)

и решим по формулам (**):
x1 b1 a13 x3 a22 a12 b2 a23 x3 a11a22 a12a21
x2 b2 a23 x3 a11 a21 b1 a13x3 a11a22 a12a21
Подставим в третье уравнение и решим его:
x |
3 |
|
a11a22b3 a12a31b2 a21a32b1 a22a31b1 a12a21b3 a32a11b2 |
|
|||||||||||||||
a a a a a a a a a a a a a a a a a a |
|||||||||||||||||||
|
11 |
22 |
33 |
12 |
23 |
31 |
21 |
32 |
13 |
13 |
22 |
31 |
12 |
21 |
33 |
23 |
32 |
11 |
|
Аналогично можно записать решение для х1 и х2, которые мы здесь опустим.
Числитель можно получить из знаменателя простой заменой членов ai3 на bi ! Т.е. при решении системы трёх уравнений всё определяется знаменателем. Запишем алгебраические члены, входящие в выражение в знаменателе как таблицу
a11a12a13
a21a22a23
a31a32a33
Эту таблицу назовём матрицей системы уравнений (***), а выражение в знаменателе - определителем этой матрицы. Для числителя аналогичная таблица чисел выглядит
a11a12b1
a21a22b2
a31a32b3
Обозначив определитель матрицы системы уравнений через , а числитель через i, получим для разыскиваемых хi простую формулу, называемую правилом Крамера
Xi = i /
Оказывается, эта формула верна для системы уравнений любого порядка.
Таким образом, для решения системы уравнений достаточно найти определитель матрицы этой системы и сделать некоторые преобразования с определителем.
Абстрагируемся от систем уравнений и назовём матрицей вообще некоторую прямоугольную таблицу чисел. Причём число строк и столбцов может быть и неодинаковым! Запишем в общем виде:
a11a12 ...a1m a21a22...a2m
..............
an1an2...anm
Употребляют и сокращённую запись:

 aij
aij 
 где i=1,... n; j,... m
где i=1,... n; j,... m
или вообще просто: A (будем употреблять мы).
Числа n и m назовем порядками матрицы n m (n строк на m столбцов). Например матрица 2 2; 2 3 и т.п.

В случае квадратной матрицы вводится понятие главной диагонали. Это элементы аii
a1 a2
Частные случаи: Матрица - столбец A a3
...
...
an
Матрица - строка 
 A
A


 aa1 2...an
aa1 2...an 

Транспонирование матрицы - это операция перестановки строк и столбцов. Обозначается операция : Т
|
a a |
|
|
|
T |
|
|
|
|
a a |
|
|
|
|
|
||||||
|
11 12 |
|
|
|
|
|
|
|
11 21 |
|
|
a21a22 |
|
|
|
|
|
|
|
|
a12a22 |
Очевидно, что транспонированная матрица-строка - это матрица-столбец и наоборот. Особую роль играют матрицы, которые при транспонировании не изменяются. Такие матрицы называются симметрическими. Бывают ленточные матрицы с шириной диагонали - k членов. Для симметрических матриц можно говорить о полуширине диагонали.
Операции над матрицами
Матрицы считаются равными, если они имеют одинаковые порядки и их соответствующие элементы совпадают.
а). Сложение матриц. Суммой двух матриц |
|
aij |
|
и |
|
bij |
одних и тех же порядков |
||||||||||||||||||||||||||
называют матрицу |
|
cij |
|
|
|
, элементы которой есть |
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
c |
a b |
i 1,...n |
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ij |
ij |
ij |
j 1,...m |
|
|||||||||
Будем писать: |
|
С=А+В |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
Непосредственно из определения вытекает : |
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||
переместительное свойство |
А+В=В+А |
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||
и сочетательное свойство |
(А+В)+С=А+(В+С) |
|
|
|
|
|
|||||||||||||||||||||||||||
б). Умножение матрицы на |
число : |
матрица |
|
|
|
aij |
|
умножается на число , получается |
|||||||||||||||||||||||||
|
|
|
|||||||||||||||||||||||||||||||
матрица |
|
|
|
cij |
|
|
|
|
|
|
|
aij |
|
|
- (каждый член умножается на ). Отсюда непосредственно следует: |
||||||||||||||||||
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||
сочетательный закон: A B A B
распределительный закон относительно суммы чисел: A A A
|
|
|
|
|
в). Перемножение матриц: произведением двух |
матриц |
aij |
i 1,...m; j 1,...n и |
|||||||||||||||
|
bij |
|
|
|
i 1,...n; j 1,... p называют матрицу |
|
|
|
cij |
|
|
|
i 1,...m; j 1,... p , где |
|
|
|
cij |
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
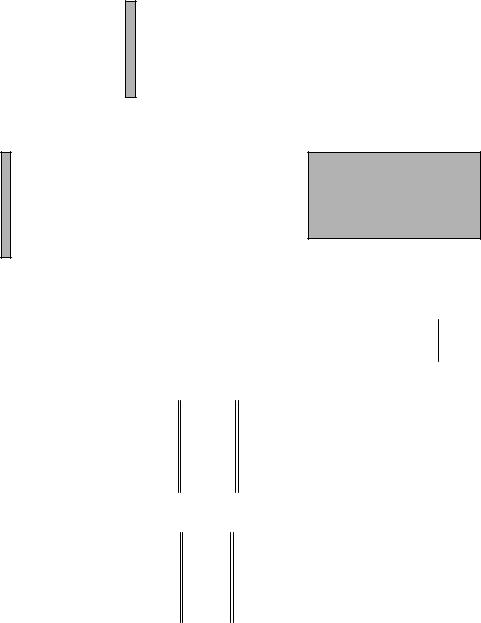
определяется из формулы:
n
cij aik bkj k 1
т.е. не всякие матрицы можно перемножить а только те, где число столбцов матрицы А равно числу строк матрицы В.
Частный случай - умножение матрицы-строки на матрицу-столбец определено, если количество членов в строке (n) равно количеству членов в столбце (n). Результатом такого умножения является число
n
|
x В n |
= С11 |
|
А
Определено всегда умножение столбца на строку:
n
m x |
|
= |
m |
|
n
Произведение двух матриц не обладает перестановочным свойством, т.е. A B B A. К примеру:
A |
01 |
B |
00 |
A B |
10 |
B A |
00 |
|
00 |
10 |
00 |
01 |
|||||
|
|
|
|
Введём важное понятие диагональной матрицы
d100...0
D0d20...0 00d3...0
000...dn
и её частный случай - единичную матрицу:
100...0
010...0
E
.........
000001
Легко увидеть, что для любой квадратной матрицы А справедливо :
E A A E A
Познакомившись с умножением матриц, можно нашу систему уравнений ***) записать компактно в матричном виде. Введём обозначения. Матрицу системы уравнений, представляющую таблицу из коэффициентов при неизвестных, обозначим А:

A 
 a11a12a13
a11a12a13 
 .
.
...........
Для неизвестных введём обозначения матрицы-столбца Х
x1
Xx2
x3
и для правых частей - 
 В
В
 .
.
Тогда можно записать:
|
A |
|
X |
|
B |
|
|
|
|
a11x1 a12 x2 a13 x3 |
|
b1 |
|||||
|
|
|||||||
|
|
................... |
|
|
|
|
|
b1 |
|
|
................... |
|
|
|
|
|
b1 |
или
a |
|
x |
|
a |
|
x |
|
a |
|
|
x |
|
|
b |
|
11 |
|
1 |
|
12 |
|
2 |
|
13 |
|
3 |
1 |
||
a21x1 |
a22 x2 |
a23 x3 |
b2 |
|||||||||||
a |
31 |
x |
1 |
a |
32 |
x |
2 |
a |
33 |
x |
3 |
b |
||
|
|
|
|
|
|
|
|
3 |
||||||
Определители
Мы уже ввели понятие определителя для матрицы 3-го порядка. Перейдём теперь к понятию определителя порядка n, где n 2.
Введём понятие минора. Минором любого элемента аij матрицы n-ого порядка называется определитель порядка n-1, соответствующий матрице, полученной из родительской матрицы вычёркиванием i-той строки и j-того столбца. Обозначим минор символом M ij (Лучше обозначить просто Мij)
a11a12...a1j...a1n a21a22...a2 j...a2n
...................
aj1aj2...aij...ain
...................
an1an2...anj...ann
К примеру у матрицы четвёртого порядка можно выделить 16 миноров:
1 2 4 6
5 3 1
7 5 3 1 1
M 1 1 1 3
8 1 1 3
2 0 4
7 2 0 4

Запишем теорему без доказательства:
Теорема 1. Каков бы ни был номер строки i (i=1,...n); для определителя n-ого порядка справедлива формула:
n
i j i
det A = 1 aij M j
j 1
Эта формула называется разложением определителя по i-той строке.
Подчеркнём, что в этой формуле показатель степени, в которую возводится (-1) равен сумме номеров строки i и столбца j, т.е. сумма может быть чётной и нечётной. Соответственно слагаемые в этой сумме могут входить в неё как со знаком (+) так и со знаком (-). Пример : (разложим по 2-й строке)
|
3 |
2 |
1 |
|
2 |
1 |
|
3 |
1 |
|
3 |
2 |
|
|
|
|
|
|
|
||||||||||
det |
2 |
1 |
3 |
2( 1) |
1 |
3( 1) |
2* 4 1( 6 2) |
|||||||
0 |
2 |
2 |
2 |
2 |
0 |
|||||||||
|
2 |
0 |
2 |
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
3(4) 8 8 12 12
Кстати, проще разложить по третьей строке:
|
3-21 |
|
-21 |
|
3-2 |
|
2 6 1 2 3 4 14 2 12 |
|
|
|
|
||||
det |
-213 |
2 |
2 |
|
|||
|
20-2 |
|
13 |
|
-2 1 |
|
|
|
|
|
|
|
|
|
К этому же результату можно прийти, воспользовавшись формулой ****) - знаменатель при вычислении х3, иначе называемой формулой “треугольника”:
det 3 1( 2) ( 2) 3 2 2 0 1 2 1 1 ( 2)( 2)( 2) (3 0 3) 6 12 2 8 12
Свойства определителей
1. Величина определителя не изменится, если строки и столбцы поменять местами, т. е. транспонировать матрицу. Доказать можно, расписав определители:
1 2 |
4 6 2 |
13 |
4 1 2 |
|
3 4 |
2 4 |
|||
|
|
2. Перестановка двух строк или двух столбцов определителя равносильна его умножению на (-1). Для доказательства достаточно расписать определитель:
3 2 |
7 2 5; |
1 4 |
2 7 5. |
|
1 4 |
3 2 |
|||
|
|
3.Если определитель имеет две равные строки или два равных столбца, то он равен 0. Это очень важное свойство. В самом деле, перестановка строк даёт: ;2 0; 0.
4.Умножение всех элементов некоторой строки на число равносильно умножению определителя на это число . Иными словами, общий множитель из некоторой строки можно выносить за знак определителя:

a11 a12 a13 a11a12a13
a21a22a23 |
.... |
a31a32a33 |
.... |
5.Отсюда вытекает, что если все элементы некоторой строки =0, то и сам определитель
равен 0.
6.Если элементы двух строк пропорциональны, то определитель равен 0.
7.Проще написать на доске:
|
|
|
|
|
|
|
|
|
|
|
a1 |
a1 |
b1 |
b1 |
c1 |
c1 |
|
a1 |
b1c1 |
|
a1b1c1 |
a2 |
|
b2 |
|
c2 |
|
|
a2b2c2 |
|
a2b2c2 |
|
a3 |
|
b3 |
|
c3 |
|
|
a3b3c3 |
|
a3b3c3 |
|
8.Если к элементам одной строки прибавить элементы другой строки, умноженной на некоторый коэффициент , то величина не изменится!
9.Непосредственно из выражения определителя следует, что величина определителя равна сумме произведений элемента на алгебраическое дополнение этого элемента.
Обратным образом: сумма произведений элементов какого-либо столбца на алгебраические дополнения другого столбца равна нулю.
Если ввести обозначение A ( 1)(i j) Mi j и назвать Аij алгебраическим дополнением |
|||||||
|
|
|
|
|
|
ij |
|
элемента аij , то последнее свойство (9) можно записать |
|||||||
|
|
|
|
|
|
|
n |
|
A |
|
ij ai1Aj1 ai2 Aj2 ain Ajn |
aik Ajk , |
|||
|
|
||||||
|
|
|
|
|
|
|
k 1 |
где ij - символ Кронекера: |
|
||||||
|
|
|
|
|
1,i |
j |
|
|
|
|
ij |
|
j |
|
|
|
|
|
|
0,i |
|
||
Лекция 2.
Обратная матрица
Пусть А - квадратная матрица. Определение: Матрица В называется обратной левой матрицей по отношению к матрице А, если
В А Е
матрица С называется обратной правой по отношению к А, если
А С Е .
Убедимся, что если матрицы В и Е существуют, то они совпадают между собой. Действительно:
B BE B(A C) (BA)C EC C
Таким образом правые и левые матрицы совпадают и они называются просто обратная матрица и обозначаются А-1. Вспомним оговорку “... если существует обратная матрица”. Какие условия следует наложить на матрицу А, чтобы существовала у неё обратная матрица?
Теорема. Для того, чтобы для матрицы А существовали левая и правая обратные матрицы, необходимо и достаточно, чтобы определитель det А матрицы А был отличен от нуля.
Необходимость: допустим матрица В существует. Тогда из соотношения АВ=Е следует: det A det B 1. Значит detA 0.
Здесь мы использовали свойство определителей: определитель произведения матриц равен произведению определителей этих матриц. Примем это без доказательства.
Достаточность. Пусть определитель detA= 0. Составим следующую матрицу В:
|
|
A11 |
|
|
|
A21 |
... |
|
An1 |
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
||||
B |
|
A12 |
|
|
|
A22 |
... |
An2 |
|||
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
||||
|
...................... |
|
|||||||||
A1n A2n ... Ann
Здесь через Aij обозначены алгебраические дополнения соответствующих элементов
aij .Убедимся, что она обратная. Умножим:
A11 |
|
|
|
|
A21 |
... |
|
|
An1 |
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
a11a12...a1n |
|
|
с11..... |
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
A12 |
|
|
|
|
A22 |
|
|
|
|
|
An2 |
|
|
|
|
|
|
|||
|
|
|
|
|
... |
|
|
|
|
a21a22...a2n |
|
......... |
|
|
||||||
|
|
|
|
|
|
|
|
|
|
......... |
|
|||||||||
...................... |
|
|
|
.............. |
|
|
|
|
||||||||||||
|
|
|
|
an1an2...ann |
|
|
|
|
||||||||||||
A1n |
|
|
|
|
A2n |
... |
Ann |
|
|
|
|
......... |
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
1
c11 a11 A11 a21 A21 L an1 An1 1
Эта сумма есть не что иное, как разложение определителя матрицы 
 А
А
 по первой строке, и
по первой строке, и
значит, эта сумма = .
1
c12 a12 A11 a22 A21 an2 An1 0
Эта сумма является суммой произведений элементов второй строки матрицы А на алгебраические дополнения первой строки! Такое произведение равно нулю!
И т.д. В итоге, только на главной диагонали останутся ненулевые члены - они равны единице. Теорема доказана.
Эта теорема нам даёт правило нахождения обратной матрицы. Надо составить вспомогательную матрицу, состоящую из алгебраических дополнений, транспонировать её и
умножить на число |
1 |
. |
|
det A
Очевидные следствия из определения обратной матрицы:
|
|
|
|
A 1 1 |
A; |
det A 1 |
1 |
|
|||
|
|
|
|
det A |
|||||||
|
|
|
|
AB 1 B 1A 1 |
|||||||
|
|
|
|
|
|
||||||
Действительно: |
|
AB |
|
B 1A 1 |
|
A BB 1 |
|
A 1 AEA 1 |
AA 1 E |
||
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|||
т.е. матрица АВ - обратная для матрицы В-1А-1. |
|
|
|||||||||
Решение систем линейных уравнений
с помощью обратной матрицы |
|
Если число уравнений равно числу неизвестных, то система уравнений |
|
АХ=В |
(*) имеет |
квадратную матрицу. Если число уравнений n, то матрица А - квадратная n-ного порядка. Если матрица А невырожденная, det A 0, то покажем, что система имеет единственное решение. Т.к.
А не вырождена, то существует обратная матрица А-1. Умножим обе части (*) на А-1:
А-1АХ=А-1В но А-1А=Е, а ЕХ=Х.
Следовательно, решение единственное и выглядит:
Х=А-1В
Понятие линейной зависимости строк |
|
|
|
|
Договоримся строку матрицы |
A a1,a2 ,...,an называть линейной комбинацией строк |
|||
B b1 ,b2 ,...,bn ...C c1 ,c2 ,...,cn , если |
для |
некоторых вещественных |
чисел ,... |
|
справедливы равенства: |
|
|
|
|
aj bj ... cj |
j 1,...n |
(*) |
||
пример: |
А=5 1 2 |
|
|
|
|
В=2 1 1 |
А=2В+С |
|
|
|
С=1 -1 0 |
|
|
|
Определение. Строки А=(а1,...,аn), В=(b1,...,bn),...С=(с1,с2,...,сn) называются линейно зависимыми, если найдутся такие числа , ,... , не все равные нулю, что справедливы равенства :
aj bj cj 0 j 1,...,n (**)
и соответственно строки называются линейно независимыми, если эти равенства возможны, когда все числа , , равны нулю.
Теорема. Для того, чтобы строки А,В,С были линейно зависимы, необходимо и достаточно, чтобы одна из них была линейной комбинацией остальных строк.
Необходимость. Пусть строки линейно зависимы, т.е. выполняется равенство (**), где хотя бы одно число не равно нулю. Для определённости положим, что 0. Тогда можно записать:
