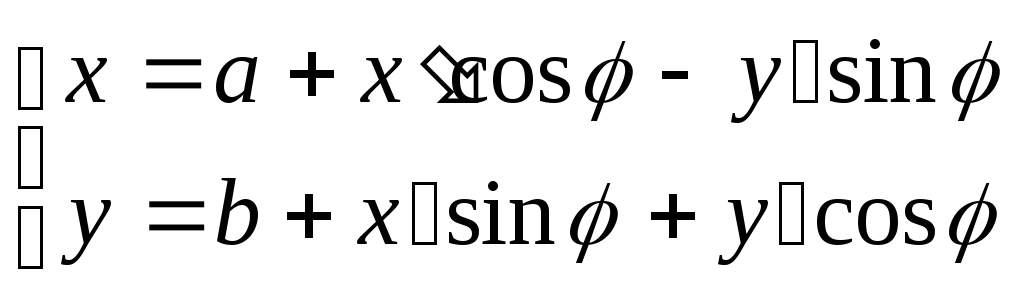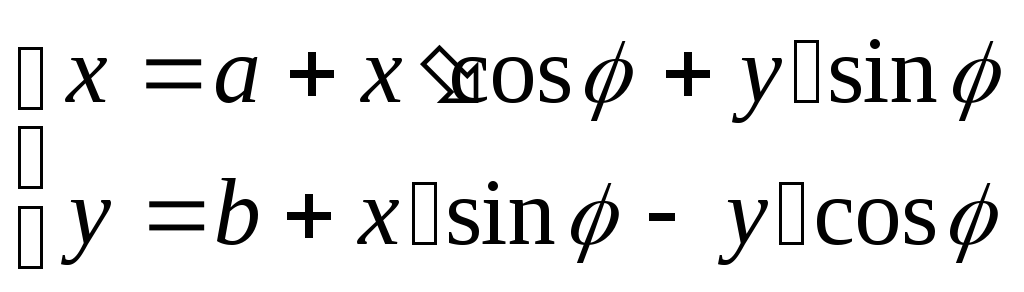Лекция 9. Преобразование декартовых прямоугольных координат на плоскости и в пространстве

П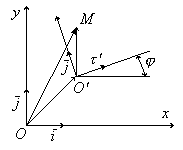усть на плоскости заданы две произвольные декартовы прямоугольные системы координат. Первая определяется началом О и базисными векторамиi j , вторая – центром О’ и базисными векторами i’ j’.

Поставим цель выразить координаты x y некоторой точки М относительно первой системы координат через x’ и y’ – координаты той же точки относительно второй системы.

Заметим, что

Обозначим координаты точки О’ относительно первой системы через a и b:

Разложим векторы i’ и j’ по базису i j:

(*)

Кроме того, имеем: . Введем сюда разложения векторов по базисуi’ j’:

отсюда

Можно сделать вывод: каковы бы ни были две произвольных декартовы системы на плоскости, координаты любой точки плоскости относительно первой системы являются линейными функциями координат той же точки относительно второй системы.

Умножим скалярно уравнения (*) сначала на i, затем на j:

(**)

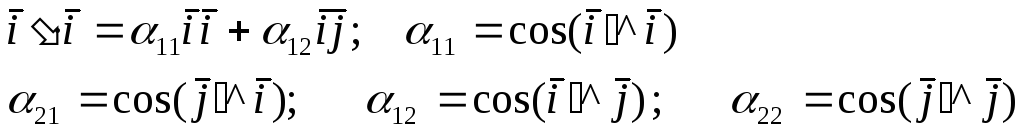О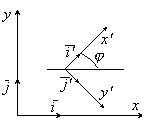бозначим через угол между векторами i и i’. Система координат i j может быть совмещена с системой i’j’ путем параллельного переноса и последующего поворота на угол . Но здесь возможен и дугой вариант: угол между базисными векторами i i’ также , а угол между базисными векторами j’j’ равен  - . Эти системы нельзя совместить параллельным переносом и поворотом. Необходимо еще и изменить направление оси у на противоположное.

Из формулы (**) получаем в первом случае:

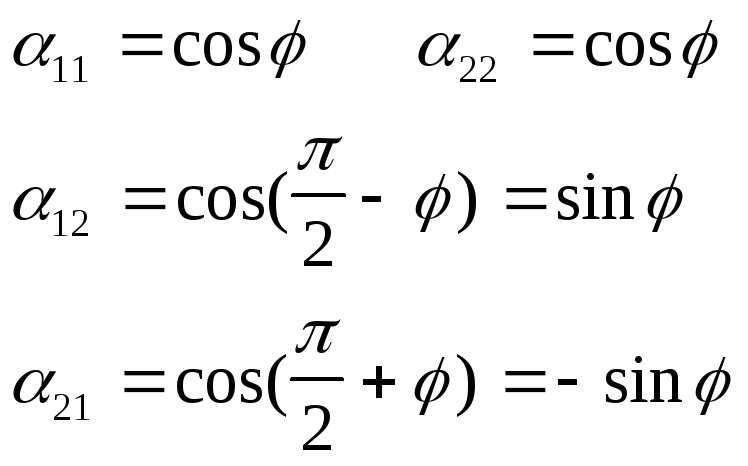
Во втором случае

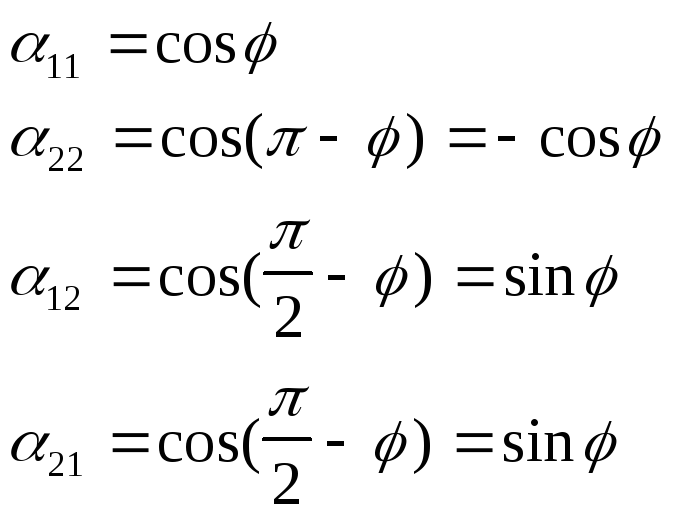
Формулы преобразования имеют вид:

1. 

2. 

Второй случай мы рассматривать не будем. Условимся считать обе системы правыми.

Т.е. вывод: каковы бы ни были две правые системы координат, первая из них может быть совмещена со второй путем параллельного переноса и последующего поворота вокруг начала на некоторый угол .

Формулы параллельного переноса:

Формулы поворота осей:

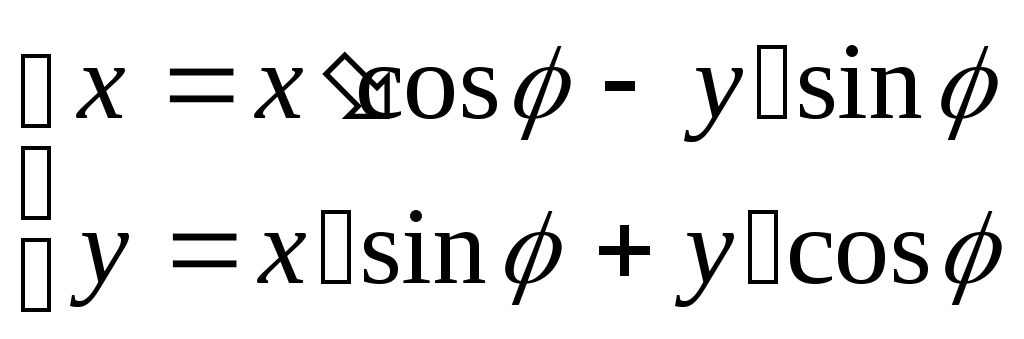
Обратные преобразования:

Преобразование декартовых прямоугольных координат в пространстве.

В пространстве, рассуждая аналогичным образом, можно записать:

(***)

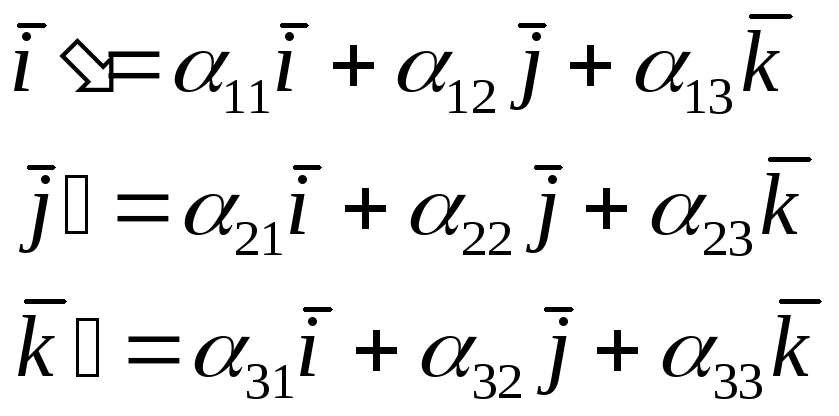И для координат получить:

(****)

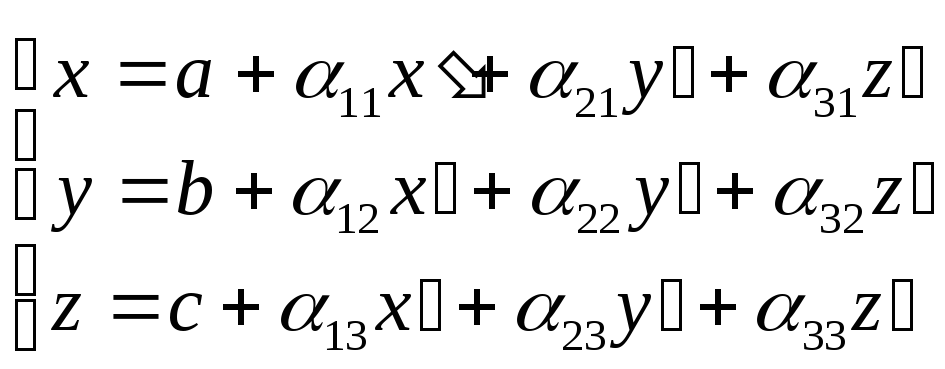Итак, каковы бы ни были две произвольные системы координат в пространстве, координаты x y z некоторой точки относительно первой системы являются линейными функциями координат x’ y’ z’ этой же точки относительно второй системы координат.

Умножая каждое из равенств (***) скалярно на i’ j’ k’ получаем:

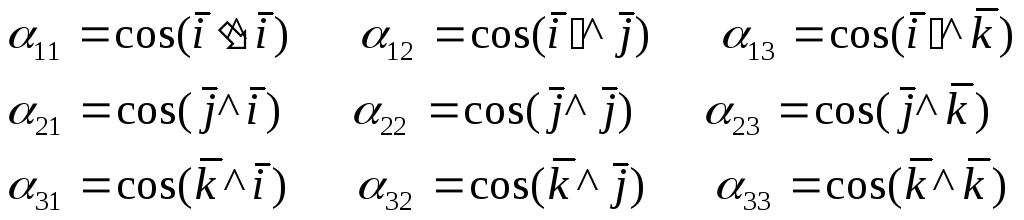
В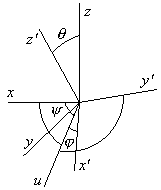ыясним геометрический смысл формул преобразования (****). Для этого предположим, что обе системы имеют общее начало:a = b = c = 0.

Введем в рассмотрение три угла, полностью характеризующих расположение осей второй системы относительно первой.

Первый угол – образован осью х и осью u, являющейся пересечением плоскостей xOy и x’Oy’. Направление угла – кратчайший поворот от оси x к y. Обозначим угол через . Второй угол  – это не превосходящий  угол между осями Oz и Oz’. Наконец, третий угол  – это угол между осью u и Ox’, отсчитываемый от оси u в направлении кратчайшего поворота от Ox’ к Oy’. Эти углы называются углами Эйлера.

Преобразование первой системы во вторую можно представить в виде последовательного проведения трех поворотов: на угол  относительно оси Oz; на угол  относительно оси Ox’; и на угол  относительно оси Oz’.

Числа _ij можно выразить через углы Эйлера. Эти формулы мы записывать не будем из-за громоздкости.

Само преобразование представляет собой суперпозицию параллельного переноса и трех проводимых последовательных поворотов на углы Эйлера.

Все эти рассуждения можно провести и для случая, когда обе системы левые, или разной ориентации.

Если имеем две произвольные системы, то, вообще говоря, можно их совместить путем параллельного переноса и одного поворота в пространстве вокруг некоторой оси. Искать ее не будем.