Матрица линейного оператора.

Пусть задан линейный оператор , переводящий x L₁ в y  L₂: .

Выберем в L₁ базис e₁ e₂ … e_n и в L₂ базис g₁ g₂ … g_m

.

Т.е. для задания оператора достаточно задать только образы базисных векторов, т.е. е₁, е₂, …, е_n.

Положим, что эти образы есть

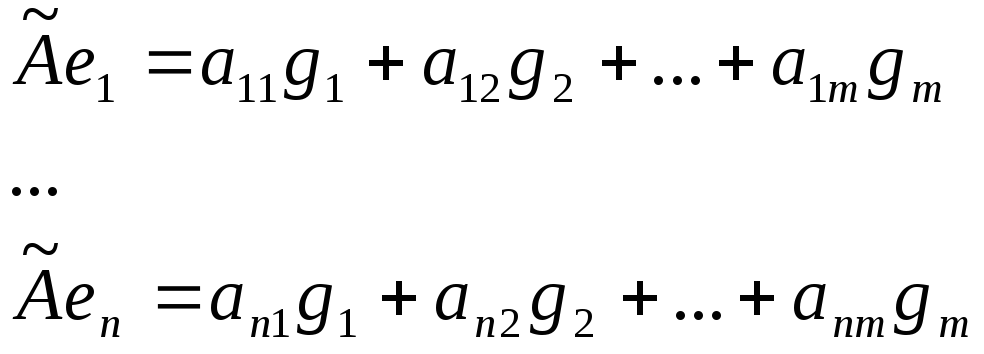
Составим матрицу:

Тогда из вышесказанного следует:

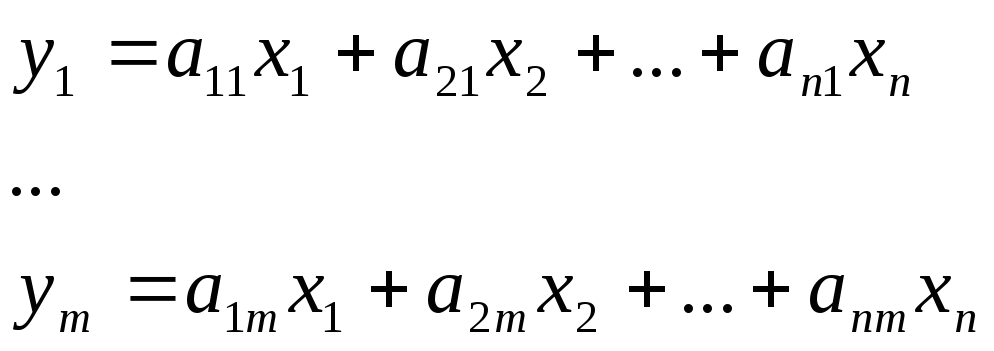
или Y = A X

Матрица А, транспонированная А^T называется матрицей линейного оператора, k-й столбец этой матрицы составлен из координат вектора е_k в базисе g₁ g₂ … g_m.

Оказывается, что некоторые характеристики этой матрицы не зависят от базисов и характеризуют внутренние свойства оператора. Так, запишем без доказательства, что ранг матрицы линейного оператора равен размерности пространства образов. Будем называть этот ранг – рангом линейного оператора. Если этот ранг совпадает с размерностью пространства L, или размерность пространства образов совпадает с размерностью пространства прообразов, то оператор назовем невырожденным.

Если множество образов и множество прообразов принадлежат одному и тому же пространству, то будем говорить о преобразовании пространства само в себя а оператор этого преобразования будем называть оператором линейного преобразования или линейный оператор. В дальнейшем мы будем рассматривать линейные операторы и употреблять термин операторы.

Изменение матрицы линейного оператора

при переходе от одного базиса к другому.

Мы уже упоминали, что матрица линейного оператора зависит от базиса. Рассмотрим вопрос о зависимости матрицы от базиса в общем случае. Пусть задан оператор у = х.

В некотором базисе {e} ему соответствует линейное преобразование Y = AX.

Введем новый базис {e^*}. Если матрица перехода есть Т, то X = TX^* Y = TY^*.

Отсюда имеем TY^* = ATX^*; Y^* = T^-1ATX^*.

Или Y^* = A^*X^*; A^* = T^-1AT.

Отметим, что матрицы А и А^* называются подобными (Т – невырожденная матрица).

Собственные числа и собственные векторы

линейного преобразования.

Ненулевой вектор х назовем собственным вектором линейного оператора , если существует такое число, что выполняется равенство: х =х.

Число  называется собственным числом или собственным значением оператора .

Т.к. оператор преобразует пространство само в себя, то матрица этого оператора квадратная. Если базис пространства {e_n}, то

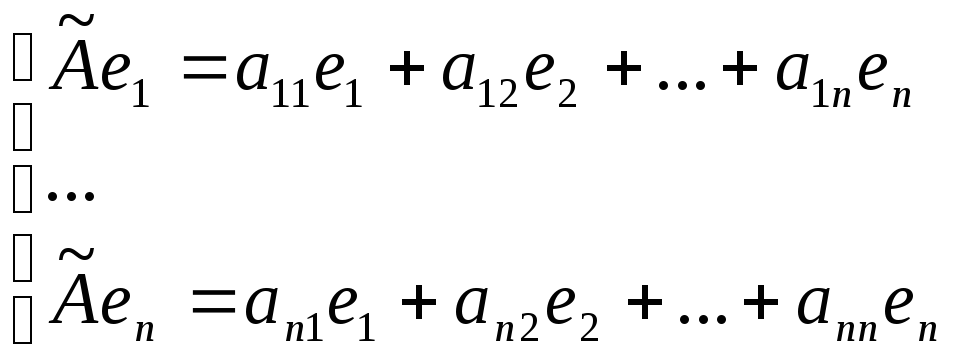
матрица оператора:

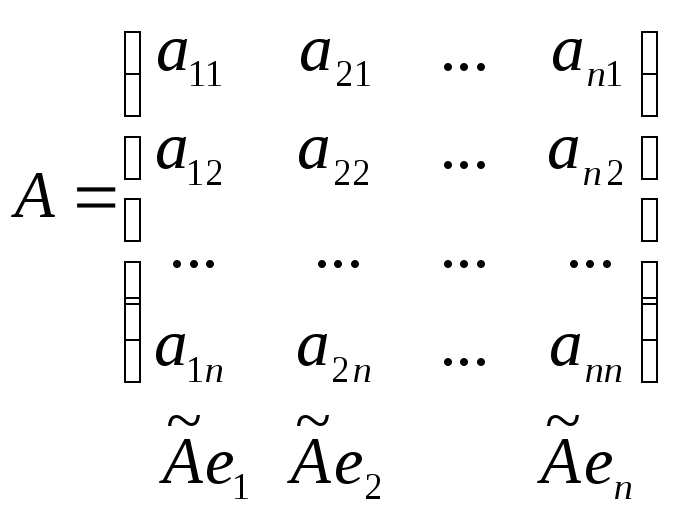
Запишем в координатной форме равенство х =х:

(-Е) х = 0

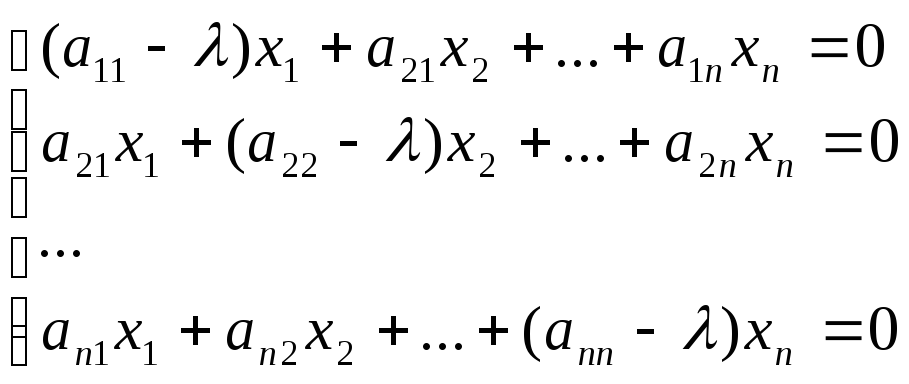
Эта система линейных однородных уравнений относительно координат искомого вектора х. Т.к. х  0, то системы должна иметь ненулевое решение. Значит, для этого, должно быть det ( A -  E ) = 0, или

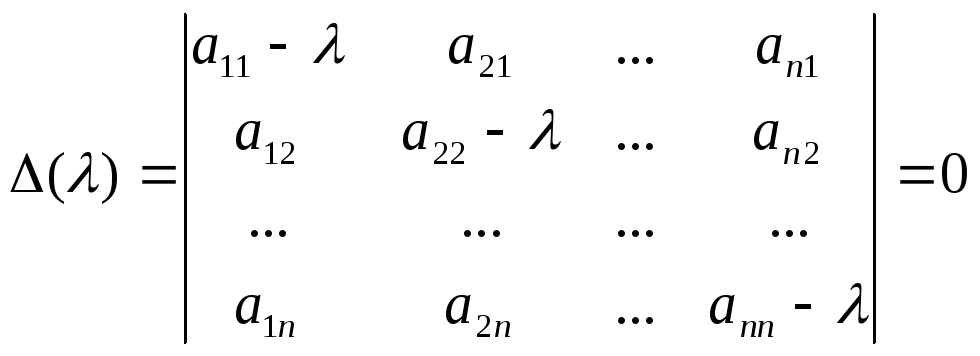
Уравнение (  ) = 0 называется характеристическим уравнением для линейного оператора , а многочлен

степени n относительно  - характеристическим многочленом.

По основной теореме алгебры, каждый многочлен степени n имеет n корней с учетом их кратности. Значит, характеристическое уравнение имеет по крайней мере один корень, т.е. каждый оператор имеет хотя бы один собственный вектор. Правда в вещественном пространстве многочлен может не иметь вещественных корней и поэтому в нашем линейном пространстве не каждый линейный оператор имеет собственные векторы.

Т.о. для нахождения собственного вектора надо составить характеристический многочлен, найти все его корни, которые будут собственными числами. После этого нужно каждое собственное число _i подставить вместо  в систему и найти все ее линейно – независимые решения. Число таких решений есть n – r_i, где r_i – ранг матрицы A - _iE. Отсюда следует, что размерность пространства собственных векторов, соответствующих одному собственному числу _i равна n – r_i.

Вспомним, что матрица линейного оператора изменяется при изменении базиса:

A^* = T^-1AT.

Найдется ли такой базис, в котором матрица А^* имела бы диагональный вид? Справедлива следующая теорема: для того, чтобы матрица А в данном базисе {e_k} была диагональной, необходимо и достаточно, чтобы базисные векторы e_k были собственными векторами этого оператора.

Доказательство: пусть e_k являются собственными векторами оператора А. Тогда

Ae_k = _ke_k (*)

А отсюда матрица А необходимо имеет вид

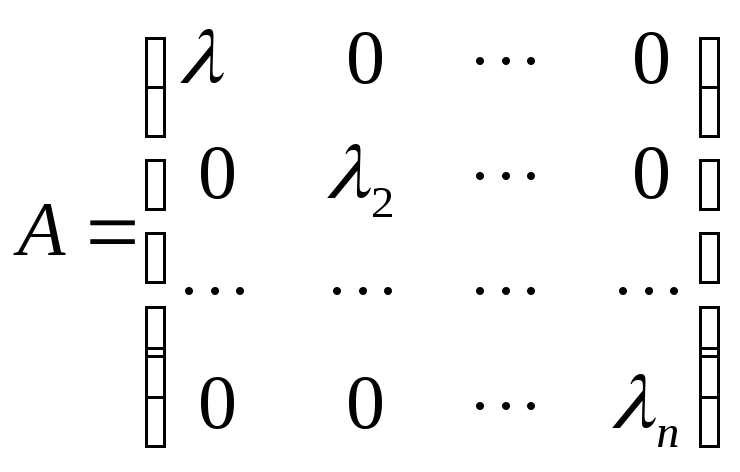
и наоборот. Пусть А – диагональная матрица оператора А в данном базисе {e_k}. Тогда соотношнния

Ae_k = ₁₁e₁+₁₂e₂+_1ne_n (k = 1,…,n)

примут вид (*), а это значит, что e_k - собственные векторы.

Запишем без доказательства свойство линейного оператора: собственные векторы линейного оператора, отвечающие различным собственным значениям, линейно независимы.

Определение: назовем оператор А, матрица которого приводится к диагональному виду, оператором простой структуры. Запишем без доказательства, что оператор имеет простую структуру в двух случаях: 1) характеристический многочлен имеет n различных корней; 2) для каждого корня _i кратности k_i ранг матрицы (A-_iE) был равен n-k_i.

Рассмотрим, чему равен определитель матрицы линейного оператора А при смене базиса.

det(A^*) = det(T^-1AT) = det(T^-1)det(A)det(T) = det(A)det(T^-1T) = det(A)det(E) = det(A)

Таким образом, можно сделать вывод, что величина определителя матрицы линейного оператора не зависит от выбора базиса. Для поиска собственных чисел линейного оператора мы составляли характеристический многочлен

Поскольку величина определителя не зависит от выбора базиса, то величины d_k являются инвариантами – не зависят от базиса. Принято называть коэффициент при ^n-1 : d_n-1 = a₁₁+a₂₂+…+a_nn следом оператора А и обозначать trA (trace – след).

trA = a₁₁+a₂₂+…+a_nn = ₁+₂+_n.

Нетрудно проследить связь между инвариантами преобразования систем координат, с которыми мы сталкивались при преобразовании уравнений поверхностей второго порядка:

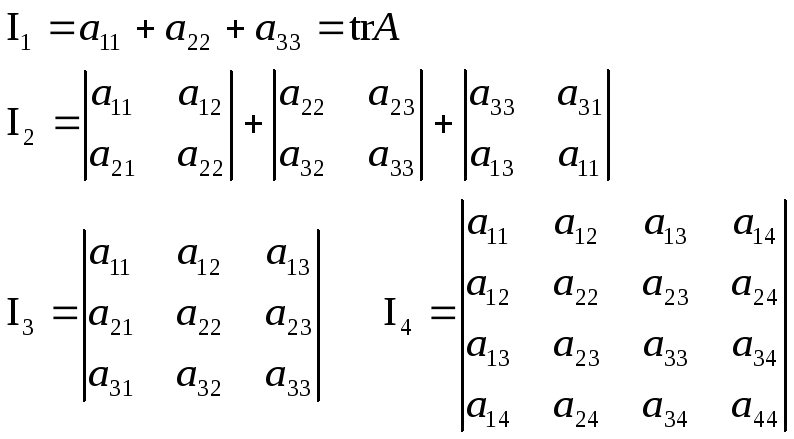
и коэффициентами характеристического уравнения d_k для линейного оператора, действующего в трехмерном пространстве , при n = 3. Учитывая это, можно записать удобную формулу для нахождения характеристического уравнения линейного оператора, дейстующего в трехмерном пространстве:

Лекция 14