Лекция 3.

Рассмотрим метод Гаусса (метод исключения неизвестных) с более общих позиций.

Запишем систему:

(*)

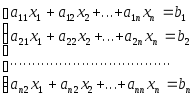Назовём элементарными преобразованиями системы уравнений (*) следующие преобразования:

1). Умножение правой и левой части одного из уравнений на произвольное число .

2). Сложение одного уравнения, умноженного но некоторое , с другим уравнением.

3). Перестановка местами двух уравнений.

Две системы уравнений, полученные одна из другой путём элементарных преобразований называются равносильными, т.е. они имеют либо одни и те же решения, либо обе эти системы не имеют решения.

Запишем матрицу системы (*), добавив справа столбец свободных членов:

Такую матрицу назовём расширенной матрицей системы линейных уравнений. Очевидно, элементарные преобразования системы линейных уравнений означают элементарные преобразования матрицы D. Эти преобразования мы проделывали ранее, вычисляя ранг матрицы. Результатом таких преобразований для матрицы D будет некоторая треугольная () матрица:

Последняя строка матрицы соответствует, очевидно, уравнению: ,

откуда .

Т.е., после привидения расширенной матрицы к виду, последнее неизвестное сразу находится. Тогда из предпоследнего уравнения найдётся х_n-1:

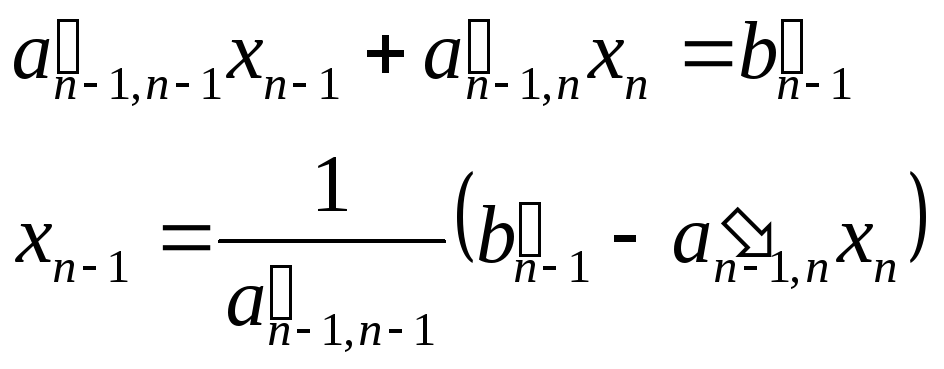
и т.д. система легко решается.

Приведение матрицы к виду называется прямым ходом метода Гаусса, а нахождение неизвестных - обратным ходом. Рассмотрим пример решения системы линейных уравнений методом Гаусса:

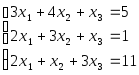
Расширенная матрица: вычитаем из первой строки вторую

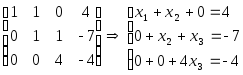
умножим первую строку на 2 и вычтем из 2^и и 3^и сложим вторую и третью

Из последнего уравнения х₃=-1.

Из второго уравнения х₂ -1=-7; х₂=-6.

Из первого уравнения х₁ -6=4; х₁=10.

Системы линейных уравнений

Рассмотрим в общем случае решение систем линейных уравнений. Дадим несколько определений.

1). Системой m уравнений с n неизвестными называется система вида:

(**)

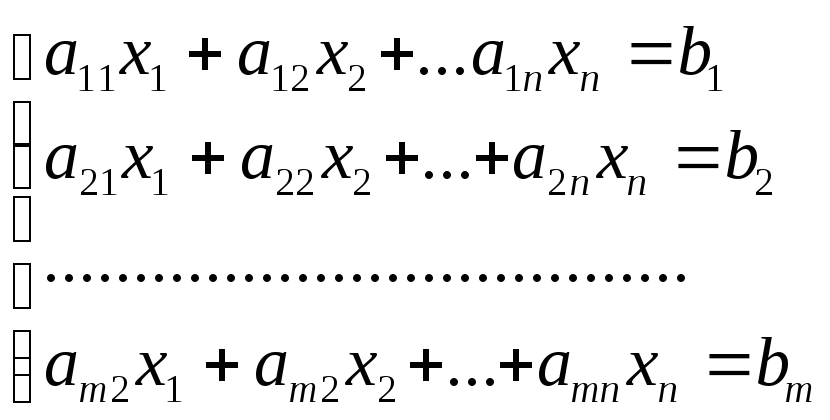2). Если в системе (**) все b_к (k=1,...m) равны нулю, то такая система называется однородной.

3). Если хотя бы один из них b_к0, то система называется неоднородной.

4). Система (**) называется совместной, если она имеет хотя бы одно решение, в противном случае она называется несовместной.

5). Совместная система линейных уравнений называется определённой, если она имеет единственное решение и неопределённой - если решений множество.

Итак, начнём с помощью элементарных преобразований сводить расширенную матрицу системы уравнений (**) к треугольному виду. Прежде всего, здесь количество уравнений не равно количеству неизвестных. Значит матрица прямоугольная и вообще говоря, к треугольной не сводится. Второй момент: Вспомним о ранге матрицы. Ранг матрицы равен количеству ненулевых строк в ступенчатой матрице, которая получится из исходной элементарными преобразованиями. Т.е. некоторые строки преобразованной матрицы могут остаться нулевыми. В итоге, после учёта этих моментов, можно записать самый общий вид преобразованной матрицы, который только может встретиться:

(***)

или, условно нарисуем:

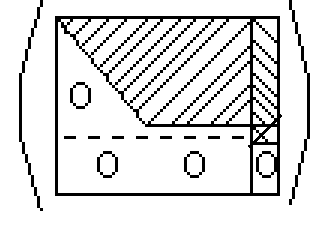
Обратим внимание на коэффициент . Может случиться, что это будет 0. А может и нет. Тогда, что невозможно. Значит решений нет, т.е. система несовместна. Поэтому на практике, сразу же после появления соотношения видаможно говорить, что система не имеет решения.

Если , то, покажем, что система имеет решение. Поскольку, то из последнего уравнения можно найти

или [] Из предыдущего уравнения можно найти

[]

и т.д. В итоге:

(****)

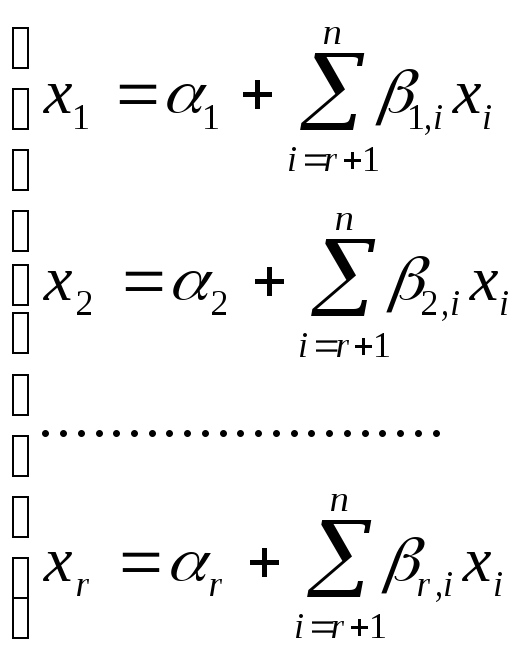из этих соотношений следует, что x_r+1,...,x_n могут принимать произвольные значения. Эти неизвестные называются свободными, а x₁,...x_r - называются основными или главными. Любая совокупность свободных неизвестных и соответствующих им основных будет решением системы. Таким образом, мы доказали теорему:

Теорема Кронекера-Капелли: для того, чтобы система уравнений (**) была совместной, необходимо и достаточно, чтобы ранг матрицы этой системы и ранг расширенной матрицы были равны.Далее, предположим мы выяснили, что система уравнений совместна. Тогда возможны два случая:

1) ранг матрицы равен количеству неизвестных R=N. Это возможно, кстати, при mn.В этом случае все неизвестные главные и они равны из (****):

Это означает, что система имеет единственное решение. Система определённая.

2) r<n. В этом случае имеются свободные неизвестные, которые можно задавать произвольно. Значит система имеет бесконечное множество решений, т.е. система неопределённая!

Пример:

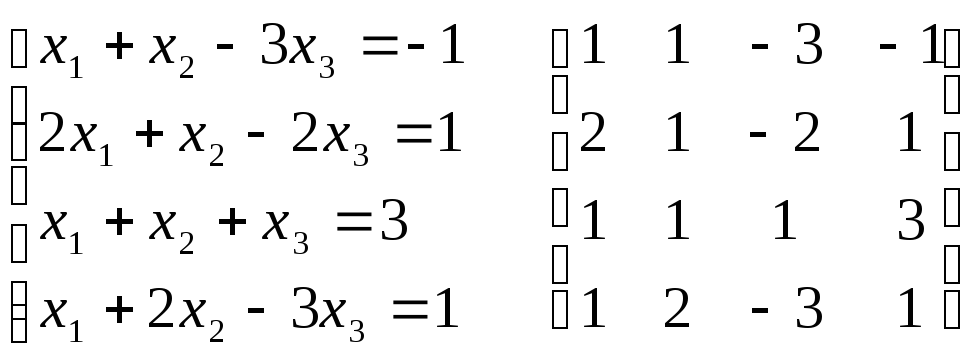
1)0 = -3 !!!

Система несовместна, решений нет!

2)

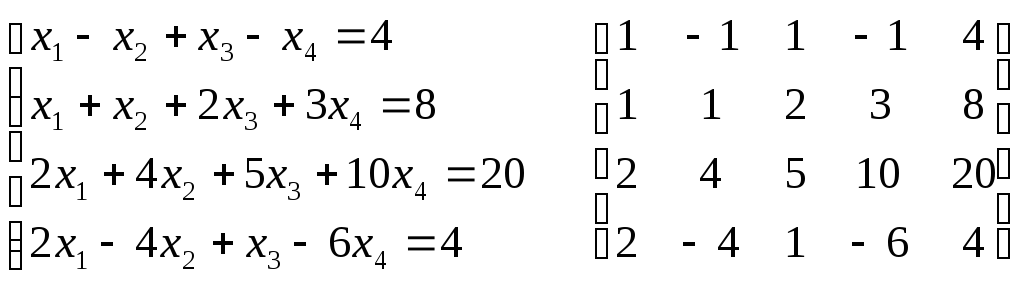
Система совместна. Положим x₃=c_1, x₄=c₂ , тогда:

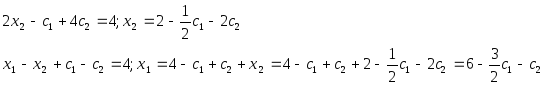
Бесконечное множество решений.

Однородная система линейных

алгебраических уравнений

Матричная запись АХ=0

Расширенная матрица отличается от матрицы самой системы наличием нулевого столбца, т.е. ранг матрицы А rang A равен рангу расширенной матрицы rang B.

r_a=r_b

Значит, по теореме Кронеккера-Капелли, система однородных линейных уравнений всегда совместна. Одно решение очевидно: x_i=0 (i=1,...,n). Это решение называется тривиальным. Следуя далее теореме Кронеккера-Капелли, придём к выводу, что если r_A=n, то решение единственное - тривиальное. Если r_A<n, то решений бесконечное множество. Рассуждая таким образом, мы доказали следующую теорему:

Для того, чтобы система однородных уравнений имела решения, отличные от нулевого, необходимо и достаточно, чтобы ранг матрицы системы был меньше числа неизвестных. Другими словами, если число уравнений равно числу неизвестных, то система имеет ненулевое решение тогда и только тогда, когда detA=0.

Очевидны следующие свойства ненулевого решения:

1). Если - решение, то- тоже решение.

2). Если - решения, то и- тоже решения.

В действительности этих свойств можно убедиться непосредственной подстановкой.

Обозначим главные неизвестные через х₁ ,...,х₂. Тогда, аналогично (****):

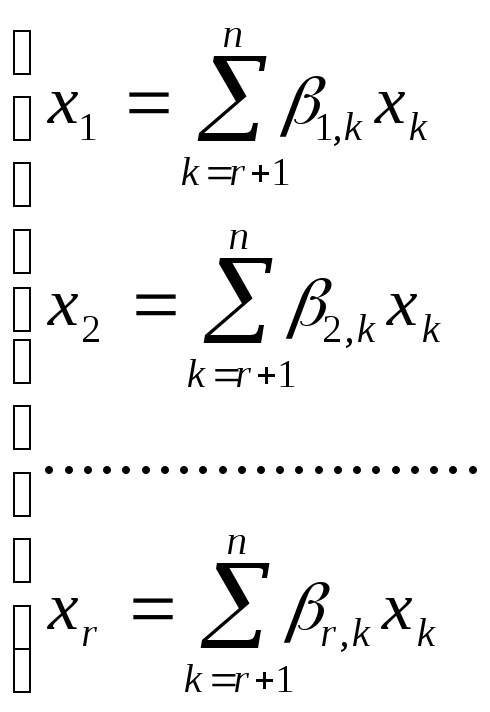В матричной форме:

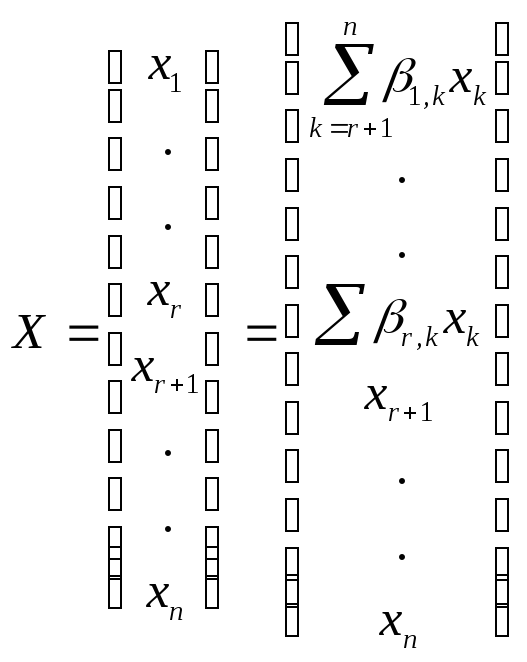
Можно записать так:

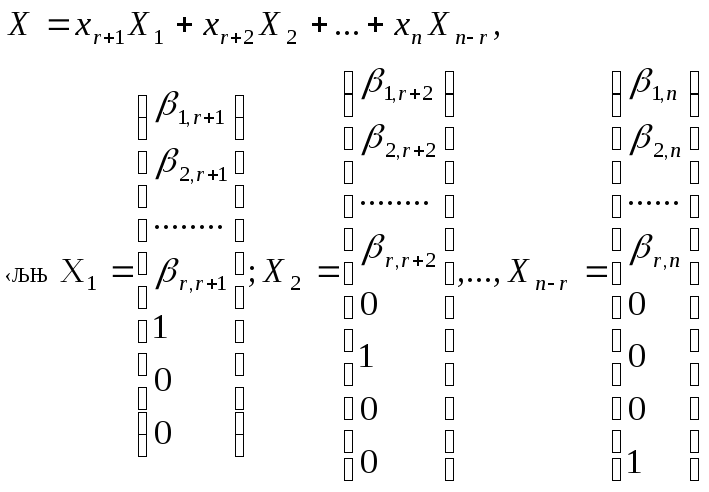
Решения X₁,X₂,…,X_n-r называются фундаментальной системой решений однородной системы. Общее решение системы X является линейной комбинацией фундаментальной системой решений

X=c₁X₁+c₂X₂+...+c_n-rX_n-r.

Пример:

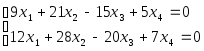
За главные неизвестные необходимо выбирать такие, при которых матрица коэффициентов не вырождена, т.е. ее определитель не равен нулю.

Возьмём за главные неизвестные х₁ и х₄, поскольку х₁ и х₂

Тогда

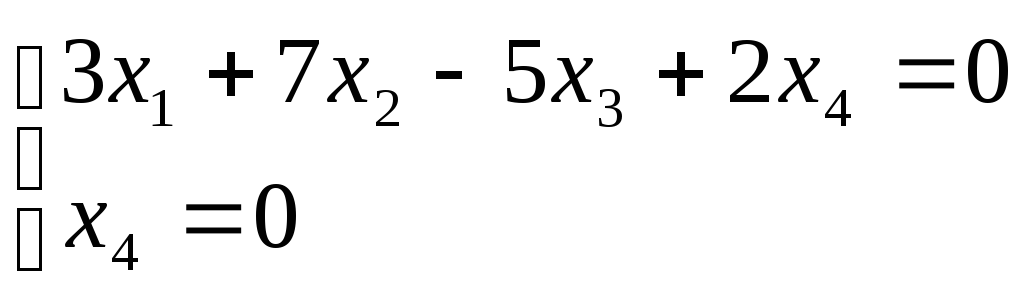
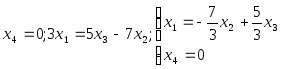
Фундаментальная система решений:

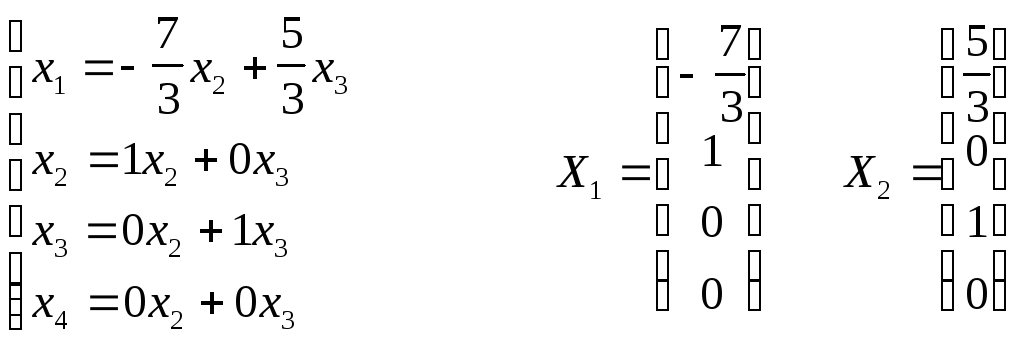
Общее решение:

X=с₁X₁+с₂X₂

Лекция 4.