Приклади розв’язання типових задач

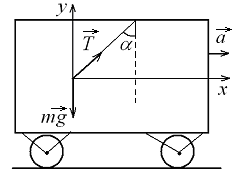
Приклад|задача| 1. У вагоні, що рухається горизонтально з|із| постійним прискоренням а = 3 м/с², висить на дроті вантаж масою m = 2 кг. Визначити силу натягу Т дроту і кут|ріг,куток| його відхилення від вертикалі, якщо вантаж|тягар| нерухомий відносно|відносно| вагону.

Розв’язання.

Рис. 2.

На вантаж|тягар| діють сила тяжіння і сила натягу дроту. Оскільки|тому що| вантаж|тягар| нерухомий відносно|відносно| вагона, його прискорення рівне прискоренню вагона. При цьому нитка повинна бути відхиленою|відхилюваною| від вертикалі назад, оскільки|тому що| тільки|лише| в цьому випадку рівнодійна|рівнодійний| сил і буде направлена|спрямований| вперед, надаючи вантажу|тягар| прискорення . Другий закон Ньютона в застосуванні|вживання| до вантажу|тягар| виразиться|викажеться,висловиться| рівнянням

Проектуючи вектори , , на осіх і у|в,біля|, отримаємо|одержимо| відповідно два скалярні рівняння:

Сумісне|спільний| рішення|розв'язання,вирішення,розв'язування| цих рівнянь і подальше|наступний| обчислення|підрахунок| дають:

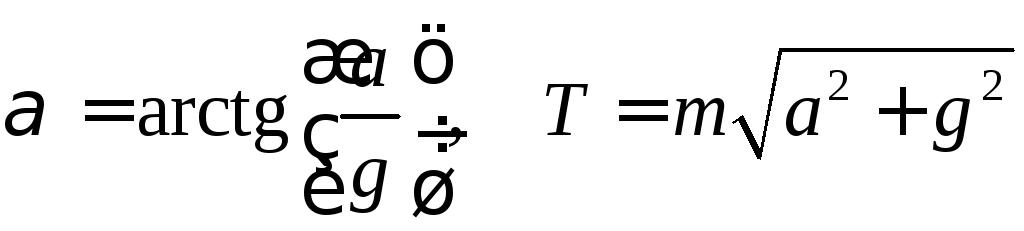
Підставивши числові значення, отримаємо

= 17^о; Т = 21Н.

Приклад|задача| 2. Груз масою т = 45 кг обертається на канаті довжиною l = 5 м в горизонтальній площині|плоскість|, здійснюючи|скоюючи,чинячи| = 16 об/хв. Який кут|ріг,куток| з|із| вертикаллю утворює канат і яка сила його натягу?

Розв’язання.

Рис. 3.

На вантаж|тягар| діють сила тяжіння і сила натягу каната. По другому закону Ньютона

(1)

Оскільки|тому що| рух по колу відбувається|походити| тут з|із| постійною по модулю швидкістю, то повне|цілковитий| прискорення тіла є нормальне прискорення а_п|, направлене|спрямований| до центру кола радіусу R:

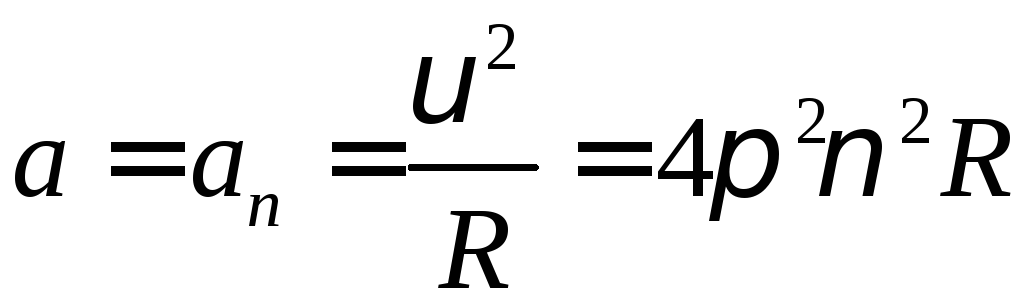
Виберемо осі х і у|в,біля| так, щоб одна з них була направлена|спрямований| у бік прискорення .

Проектуючи вектори, що входять в рівняння (1) на ці осі, отримаємо|одержимо|:

, (2)

(3)

З|із| рисунка видно|показно|, що . Вирішивши|розв'язавши| спільно рівняння (2), (3) з урахуванням|з врахуванням| останньої рівності, маємо

; .

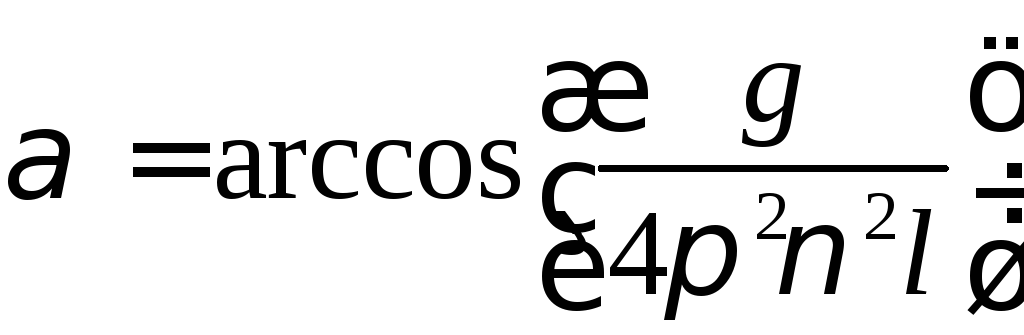Підставивши числові значення величин в одиницях СІ і виконавши обчислення|підрахунок|, знаходимо|находити|:

|Т = 0,63 кН, = 0,71,= 45°.

Приклад|задача| 3. Визначити прискорення a₁ і a₂, з|із| якими рухаються|сунуться| вантажі|тягар| m₁ і m₂ в установці, зображеній|змальованій| на рис. 4, а також силу натяг Т нитки. Тертям і масою блоків знехтувати. Нитку вважати|лічити| невагомою і нерозтяжною.

Розв’язання.

Рис. 4.

На вантаж|тягар| m₁ діють сили тяжіння m₁g і сила натягу Т₁ нитки, на вантаж|тягар| m₂ – сила тяжіння m₂g і сили натягу Т₂, Т₃ ниток. При цьому Т₁ = Т₂ =Т₃ = Т Оскільки всі сили направлені|спрямований| по вертикалі, запишемо рівняння, що виражають|виказувати,висловлювати| другий закон Ньютона, стосовно вантажів|тягар| відразу в скалярному вигляді|вид|, вибравши позитивним напрям|направлення| вниз і припустивши|передбачивши|, що прискорення вантажу|тягар| m₁ направлене|спрямований| вниз і, отже, прискорення вантажу|тягар| m₂ – вгору|угору|:

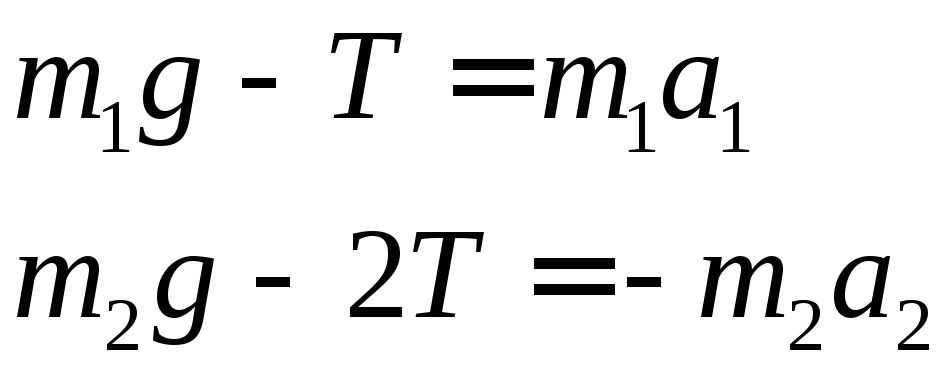
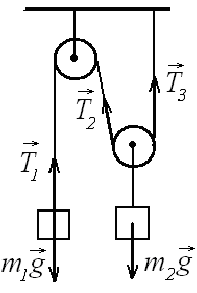
Розглядаючи|розглядуючи| кінематичну схему установки і враховуючи умову «неростяжності»| нитки, запишемо співвідношення між модулями переміщень вантажів|тягар|, які відбуваються| за один і той же час: . Очевидно, таке ж співвідношення існує і між модулями прискорень вантажів|тягар|:

Вирішивши|розв'язавши| спільно попередні рівняння отримаємо|одержимо|:

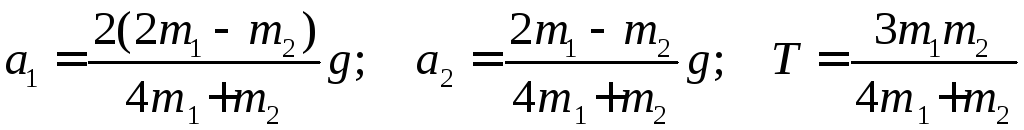
Звідси слідує|прямувати|:

1) якщо 2m₁ > m₂, то а₁ > 0, а₂ > 0, тобто прискорення вантажів|тягар| направлені|спрямований| так, як ми припустили|передбачили|;

2) якщо 2m₁ = m₂, то а₁ = а₂ = 0 – вантажі|тягар| перебувають у стані спокою або рухаються|сунуться| рівномірно;

3) якщо 2m₁ < m_2, то а₁ < 0, а₂ < 0. В цьому випадку прискорення вантажу|тягар| m₁ направлене|спрямований| вгору|угору|, прискорення вантажу|тягар| а₂ – вниз.

Зауваження.У всіх трьох випадках напряму|направлення| швидкостей вантажів|тягар| залишаються невизначеними|неозначений|, оскільки|тому що| вони залежать від напрямів|направлення| початкових швидкостей і часу руху. Наприклад, при 2m₁ > m₂ вантаж т₁ може рухатися|сунутися| прискорено вниз або сповільнено|уповільнено| вгору|угору|. В обох випадках вектор а₁ направлений|спрямований| вниз.

Приклад|задача| 4. Візок масою М = 20 кг, на якому лежить вантаж|тягар| масою m = 10 кг, тягнуть з силою F, направленою|спрямований| горизонтально. Коефіцієнт тертя між вантажем|тягар| і візком µ = 0,1. Нехтуючи тертям між візком і дорогою, знайти прискорення візка а₁ і вантажу|тягар| а₂, а також силу тертя між вантажем|тягар| і візком в двох випадках: 1) F = 2 кгс|, 2) F = 6 кгс.

Розв’язання.

Рис. 5.

Розглянемо|розгледимо| сили, що діють на обидва тіла. При цьому, оскільки їх прискорення направлені|спрямований| по горизонталі, досить враховувати лише сили, що діють горизонтально, оскільки|тому що| інші – направлені|спрямований| по вертикалі – зрівнова­жується|зрівноважується,урівноважується|.

На візок діють сила F і сила з боку вантажу|тягар| F_тр1. Остання направлена|спрямований| протилежно до|супроти| швидкості візка відносно вантажу|тягар| при терті ковзання або проти|супроти| сили F при терті спокою, тобто у будь-якому випадку|в будь-якому разі| сила F_тр1 направлена_{|спрямований|} вліво. На вантаж|тягар| діє сила тертя з боку візка F_тр2, направлена|спрямований|, згідно з третім законом Ньютона, вправо|вправо|, причому по модулю |. Направивши|спрямувавши,скерувавши| вісь проекцій у бік прискорення, тобто по горизонталі управо|вправо|, запишемо у скалярному вигляді|вид| рівняння руху візка і вантажу|тягар|:

(1)

(2)

Рівняння (1), (2) містять|утримувати| три невідомих. Щоб отримати|одержати| ще одне рівняння, з’ясуємо характер|вдача| сили тертя між візком і вантажем|тягар|. Якщо візок вислизає з-під вантажу|тягар|, то між ними діє сила тертя ковзання. Оскільки|тому що| в даному випадку сила N рівна по модулю силі тяжіння вантажу|тягар|, то

(3a)

Якщо ж візок і вантаж|тягар| рухаються|сунуться| як одне ціле, то між ними діє сила тертя спокою _|. Проте|однак| в цьому випадку виконується рівність

(3б)

Таким чином, в обох можливих випадках отримаємо|одержимо| систему трьох рівнянь.

Отже, необхідно з’ясувати характер|вдача| сил тертя, що діють між тілами. Розглянемо|розгледимо| докладніше обидва можливі варіанти:

а) візок вислизає з-під вантажу|тягар|. Між ними діє сила тертя ковзання, яку знайдемо за формулою (3а):

= 9,8 Н;

б) візок і вантаж|тягар| рухаються|сунуться| як одне ціле, утримуються тертям спокою. Тоді, позначивши а₁ = а₂ = а, запишемо систему рівнянь (1), (2) у вигляді

|вид|

вирішивши|розв'язавши| цю систему, отримаємо|одержимо|

(4)

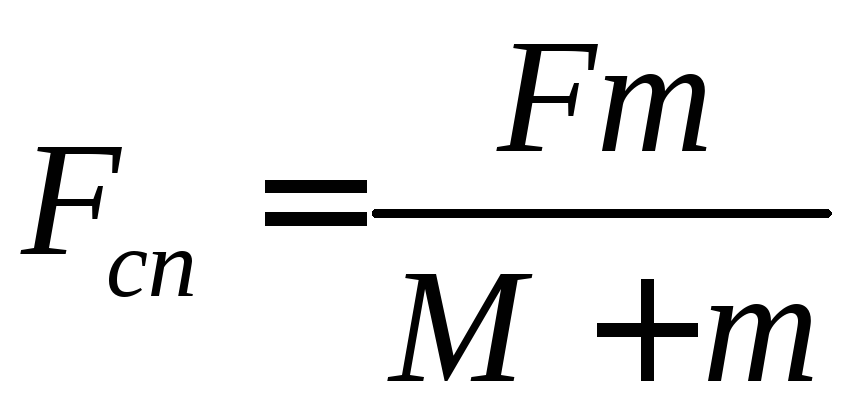(5)

Формула (5) виражає|виказувати,висловлювати| пропорційну|пропорціональний| залежність між F і F_сп. Проте|однак| значення F_сп| має межу, рівну силі F_тр яка вже знайдена. Тому насправді два тіла рухатимуться|сунутимуться| як одне ціле лише при таких значеннях сили F, при яких значення F_сп|, визначене за формулою (5), не перевищуватиме її граничного значення. Виконавши|проробивши| розрахунки, отримаємо|одержимо|:

1) якщо F = 2 кгс| = 19,6 Н, то F_сп| = 6,5 Н;

2) якщо F = 6 кгс| = 58,8 Н, то F_сп| = 19 Н, що неможливо, бо граничне значення F_сп рівне 9,8 Н.

Значить, в цьому випадку між тілами діятиме тертя ковзання. Тепер легко відповісти на всі питання завдання|задача|:

1) Р = 19,6 Н. Між тілами діє сила тертя спокою F_сп = 6,5 Н. З формули (4) знаходимо|находити| а = 0,65 м/с²;

2) F = 58,8 Н. Між тілами діє сила тертя ковзання F_тр = 9,8 Н. Із (1) і (2) знаходимо|находити| прискорення тіл: а₁ = 2,5 м/с², а₂ = 0,98 м/с².