23. Метод Ньютона. Геометрическая интерпретация. Теорема о сходимости метода в одномерном случае.

Пусть снова задано уравнение f(x)=0. Запишем его тождественно в виде ,

где , и положим.

Пусть х_к – некоторое приближение к корню х*. Для ускорения сходимости итераций желательно, чтобы был как можно меньше. Положим

Отсюда находим, что . Подставляя в исходное уравнение, получаем рекуррентную формулу:

, . (11)

Это и есть итерационная процедура Ньютона.

Метод Ньютона известен и под другим названием: метод касательных. Дадим графическую иллюстрацию данного метода.

Пусть и строго выпукла (т.е.). Пусть, кроме того,- единственный корень функциина промежутке.

В качестве начального приближения возьмем точку , такую, для которой. Проведем через точку на плоскостикасательную к кривой. Запишем уравнение касательной:. В качестве следующего приближения возьмем точку, в которой. Отсюда находим

. Далее в точке графика проводим новую касательную, и т.д. В результате получаем итерационную процедуру Ньютона (11).

Метод касательных проиллюстрирован на рис.3.2.

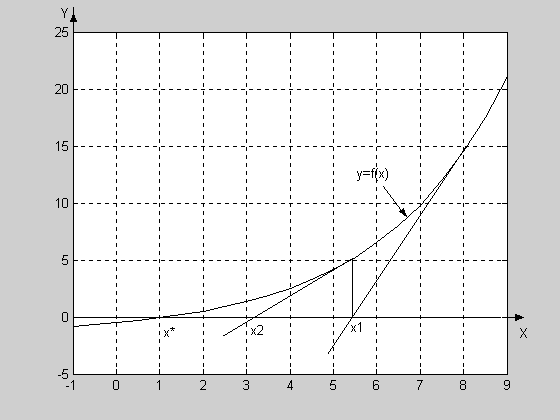
Рис.3.2. Графическая иллюстрация метода Ньютона (метода касательных). Начальная точка x₀ = 8. Точное значение корня x* = 1. x₁ и x₂ – два последовательных приближения к корню, полученные с помощью касательных.

Исследуем условия сходимости метода Ньютона.

Теорема 3.5. Пусть ,на, иимеет единственный действительный корень на. Тогда, такое, что на множестве

процедура Ньютона (11) сходится к точке со скоростью геометрической прогрессии, а в некоторой малой окрестности точкиx^* и с квадратичной скоростью, т.е. :

В силу непрерывности функций на [a,b], обе производные ограничены поэтому , причемпо условию.

Заметим, что итерационная процедура (11) равносильна методу простых итераций для уравнения

(12)

Очевидно, что является неподвижной точкой функционального оператора, называемогооператорной функцией Ньютона-Рафсона. Проверим условия сжатости данной функции. Для этого вычислим и оценим производную . Имеем:

.

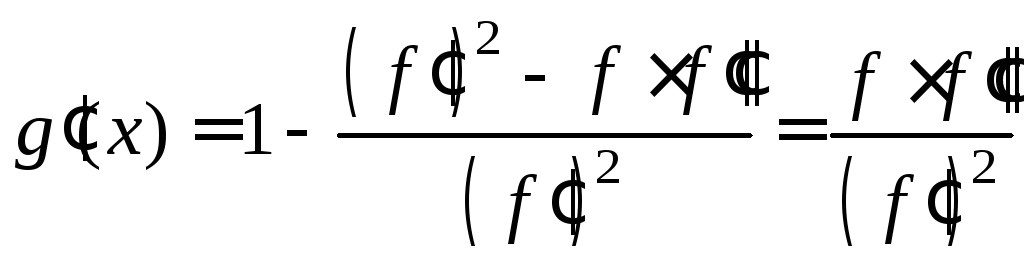Оценивая полученное равенство по модулю, и учитывая условия теоремы, получим

(13)

Поскольку - корень уравнения, то, как следует из неравенства (13),

и близка к нулю в некоторой малой окрестности точки , где и следует ожидать выполнения условия сжатости.

Запишем формулу конечных приращений Лагранжа

.

Оценивая по модулю, получаем

.

Подставляя эту оценку в (13), получаем:

.

Условие сжатости будет, очевидно, выполнено, если

. (14)

Обозначив , получаем конкретизацию окрестности, где выполняется одно из условий сжатости. Пусть теперь найдено-е приближение к корню.

Так как по условию теоремы непрерывна на, то справедливо тэйлоровское разложение функциис центром в точкес остаточным членом в форме Лагранжа

Положим в последнем равенстве :

.

Выражая отсюда , получим:

(15)

Вычтем (15) из (11):

;

Оценивая последнее равенство по модулю, получаем:

(16)

Продолжим далее оценку по модулю, используя (14):

.

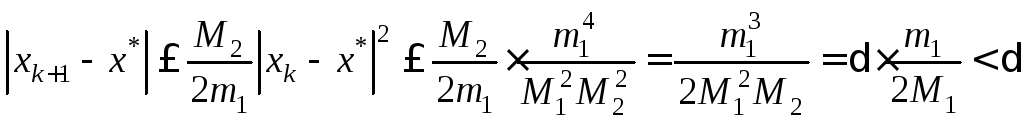Таким образом, если , гдеопределяется из неравенства (14), то точка. Следовательно, выполняется и второе условие теоремы 3.4, а значит последовательностьсходится к корнюсо скоростью геометрической прогрессии (т.е. линейно). Далее из неравенства (16) следует, что как только при некоторомвыполнится условие, так в дальнейшем, присходимость становится квадратичной:

.