1.7.2. Простейшие свойства многочленов Чебышева.

1. Многочлены Чебышева ортогональны на отрезке с весом.

Рассмотрим интеграл

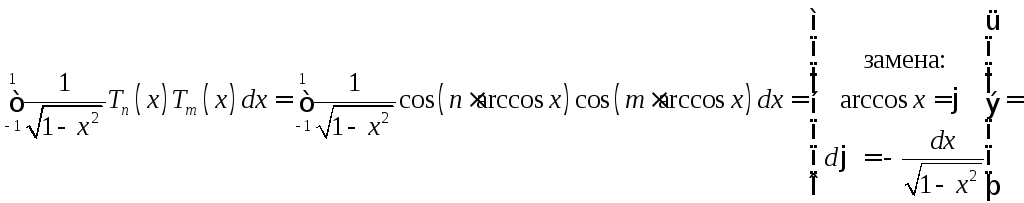
в силу ортогональности системы функций на отрезке.

Вычислим квадрат нормы:

.

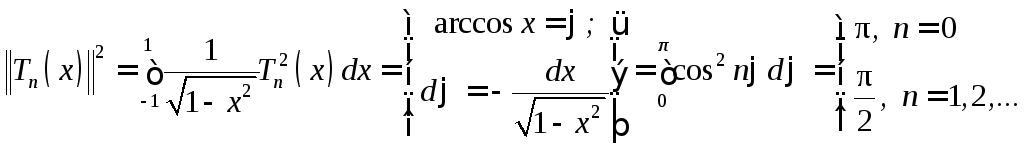2. При четных (нечетных) n многочлен Чебышева T_n(x) содержит только четные (нечетные) степени х, т.е. является четной (нечетной) функцией.

Доказывается по индукции с помощью рекуррентной формулы (25).

3. Коэффициент при старшей степени xⁿ многочлена T_n(x) равен 2^n-1.

Доказывается по индукции с помощью рекуррентной формулы (25).

4. Многочлен T_n(x) имеет на отрезке ровноn различных действительных корней, определяемых формулой:

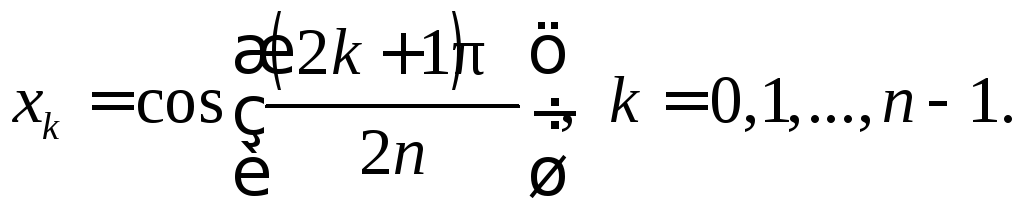
Действительно:

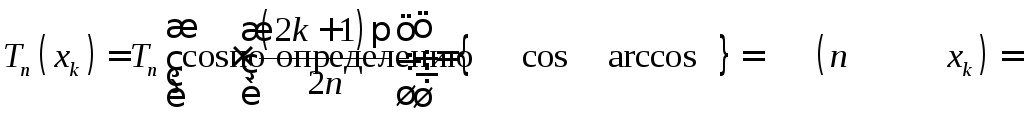
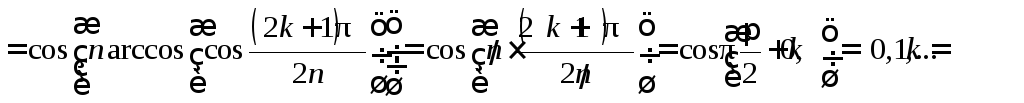
_5. и достигается в точках экстремума:

.

Из определения (1) следует, что для любого. Очевидно, что

.

6. Многочлен среди всех многочленовn-ой степени с коэффициентом при старшей степени a_n=1 обладает тем свойством, что

.

(26)

Доказывается от противного: пусть это не так и существует многочлен

такой, что выполняется противоположное:

.

(27)

Разность () – многочлен -ой степени, причем в силу (4)

.

Обозначим и заметим что, в силу (27)

.

Продолжим рассмотрение разности:

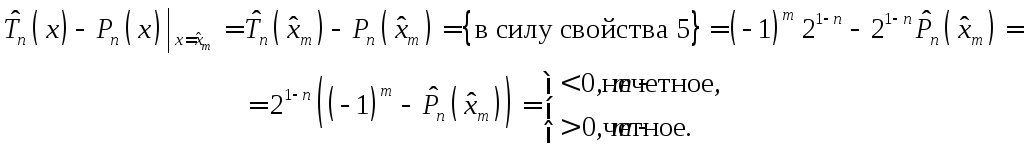
Таким образом, при переходе от точки кразность() меняет знак. Всего при переходе от точки кпроизойдет ровноn смен знака. Отсюда следует, что разность имеет на отрезкеровноn действительных корней (нулей), что противоречит теореме Гаусса, т.к. это многочлен -ой степени.

Замечание. Благодаря свойству 6 многочлен Чебышева называетсямногочленом, наименее отклоняющимся от нуля.

9. Применение многочленов Чебышева к задаче интерполяции. Теорема об оптимальном выборе узлов.

Теорема 1.3. Пусть , тогда наименьшая максимальная абсолютная погрешность интерполяции полиномом Лагранжана отрезкедостигается при выборе в качестве узлов интерполяции нулей функции

Обозначим - корень многочлена. Согласно свойству 4

(28)

Пусть – некоторая система узлов на. Запишем формулу максимальной абсолютной погрешности интерполяции по Лагранжу (формула (10) тз п.п.1.4):

,

где ,

Как следует из свойства 6:

.

Выберем в качестве узлов точки , определяемые формулой (28). Тогда

.

Отметим, что многочлен имеет одну и ту же степеньn+1, что и , один и тот же коэффициент при старшей степении одни и те же нули на.

Отсюда немедленно следует, что , и соответствующая оценка погрешности:

.

Данная оценка является наилучшей среди всех возможных способов выбора узлов интерполяции.

Замечание. Для оптимальной интерполяции на произвольном конечном отрезке [a;b] предварительно необходимо сделать линейное преобразование:

и преобразовать формулу для нулей функции к следующему виду:

,

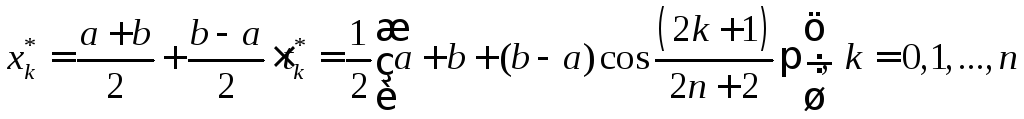11. Численное интегрирование. Использование функциональных рядов.

Пусть . Тогда существует определенный интеграл

,

согласно формуле Лейбница.

Однако, во многих случаях первообразная не выражается в аналитическом виде, поэтому приходится применять те или иные численные методы.

Примеры «неберущихся» интегралов:

–интегральный синус;

–интеграл вероятности;

- интеграл Френеля, и другие.

Одним из способов численного интегрирования является разложение подынтегральной функции в те или иные ряды (например, в ряд Тейлора) и почленное интегрирование полученного ряда. Например, для «интегрального синуса» получаем с помощью тейлоровского разложения:

.

Взяв конечное число членов разложения, получим приближенное значение интегрального синуса . При этом абсолютная ошибка приближения оценивается по остаточному члену тейлоровского разложения.