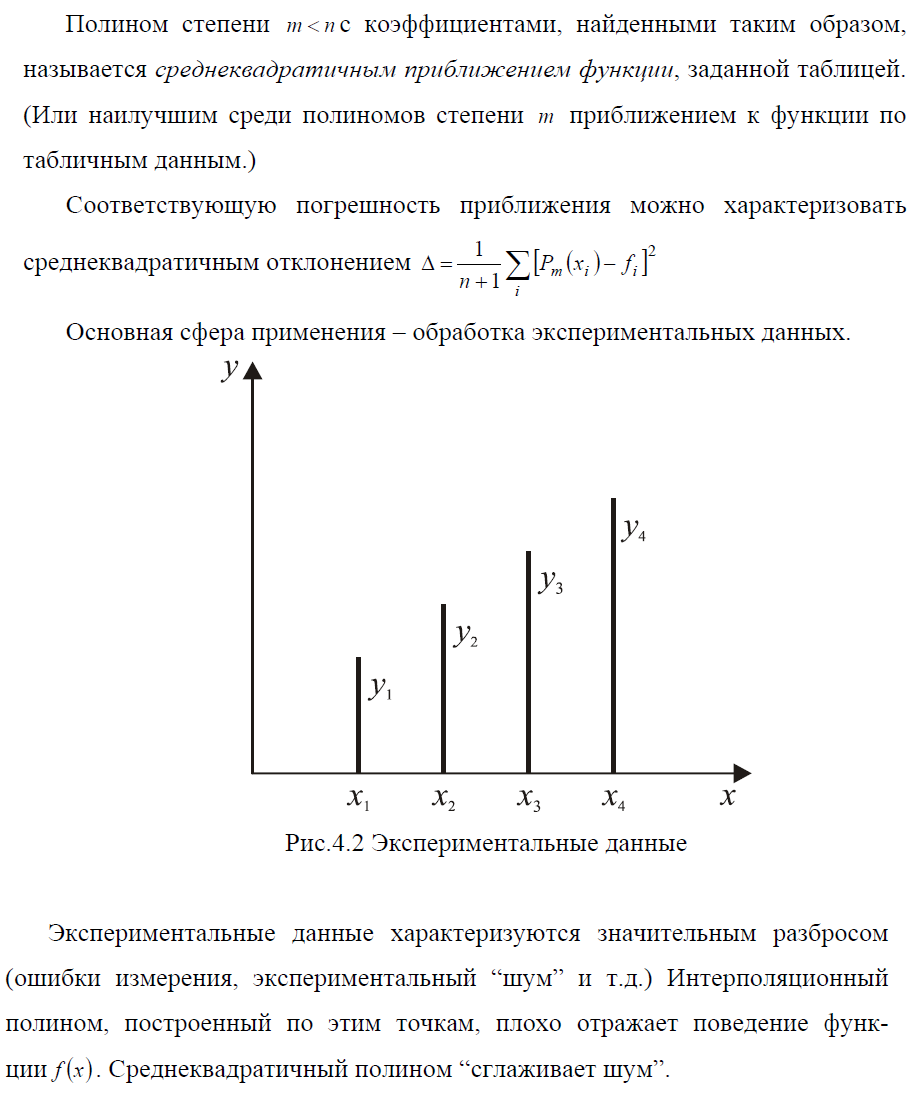
- •Определение 2. Величина называется абсолютной погрешностью представления числа X с помощью числа .
- •1.2 Распространение ошибок округления в арифметических операциях.
- •1.7.2. Простейшие свойства многочленов Чебышева.
- •11. Численное интегрирование. Использование функциональных рядов.
- •12. Квадратурные формулы на основе интерполяции. Формулы для коэффициентов и остаточного члена.
- •13. Базовые квадратурные формулы прямоугольников, трапеций и парабол. Формулы теоретической погрешности.
- •14. Обобщенные квадратурные формулы трапеций и Симпсона
- •15. Теоретические оценки погрешности обобщенных формул трапеций и Симпсона.
- •17. Общие свойства полиномов ортогональных с весом.
- •18. Алгебраическая степень точности квадратурной формулы. Квадратурные формулы Гаусса-Кристоффеля.
- •19. Теорема о необходимых условиях выбора узлов в формулах Гаусса-Кристоффеля.
- •20. Классические ортогональные многочлены. Построение ортогональных многочленов Лежандра на каноническом отрезке [-1,1].
- •2. Покажем, что - неподвижная точка. Из сходимостиследует, т.Е.
- •22. Метод простых итераций решения функциональных уравнений и систем. Условия сходимости.
- •23. Метод Ньютона. Геометрическая интерпретация. Теорема о сходимости метода в одномерном случае.
- •24. Метод Ньютона в многомерном случае. Организация итерационного алгоритма.
- •25. Численные методы решения слау. Прямые и итерационные методы – общие понятия.
- •26. Нормы вещественных квадратных матриц. Спектральные свойства матриц.
- •27. Обусловленность матриц и систем лау. Определение числа обусловленности.
- •28. Метод итераций для слау второго рода. Теорема о достаточных условиях сходимости.
- •29. Спектральный признак сходимости (теорема о необх. И достат. Условиях сходимости).
- •30. Стационарные итерационные процедуры. Приведение слау первого рода к системе второго рода.
- •31. Метод простых итераций Ричардсона. Условия сходимости.
- •32. Теорема о выборе ускоряющего множителя в методе Ричардсона.
- •33. Метод Якоби. Организация алгоритма. Теорема о достаточных условиях сходимости.
- •34. Метод Зейделя как ускорение метода Якоби. Организация алгоритма. Теорема об условиях сходимости.
- •35. Метод последовательной верхней релаксации. Организация алгоритма.
- •36. Численное дифференцирование на основе интерполяции.
- •37. Численное дифференцирование на равномерной сетке, основанное на тэйлоровском разложении. Теоремы об аппроксимации первой и второй производной.
- •38. Задача Коши. Постановки задачи в одномерном случае для первой и второй производной. Сведение к системе уравнений с первой производной.
- •39. Метод Эйлера. Алгоритм, геометрическая интерпретация, порядок точности.
- •40. Методы Рунге-Кутты повышенной точности. Метод “предиктор – корректор” и метод «средней точки».
- •41. Общая постановка краевой задачи для оду 2-го порядка. Классификация граничных условий.
- •42. Метод “стрельбы” решения краевой задачи с граничными условиями первого рода.
- •43. Метод конечных разностей решения линейной краевой задачи для оду 2-го порядка.
- •45. Устойчивость разностных схем. Спектральный признак устойчивости для уравнений с постоянными коэффициентами. Примеры для оду и уравнений в частных производных.
- •16. Правило Рунге практической оценки погрешности квадратурной формулы Симпсона.
- •10. Среднеквадратичное приближение. Метод наименьших квадратов в регрессионном анализе. Вывод уравнения прямой регрессии.
45. Устойчивость разностных схем. Спектральный признак устойчивости для уравнений с постоянными коэффициентами. Примеры для оду и уравнений в частных производных.
Определение.
Говорят, что разностная схема устойчива
по правой части, если малые возмущения
сеточной функции
![]() приводят к малому изменению сеточного
решения
приводят к малому изменению сеточного
решения![]() .
Близость оценивается в сеточной норме
.
Близость оценивается в сеточной норме![]() .
.
В общем случае произвольной К.Р.-схемы исследование устойчивости представляет собой сложную проблему. Наиболее просто решается эта задача для К.Р.-схем с постоянными коэффициентами. Для ОДУ второго порядка конечно-разностная схема получается из общего уравнения
![]() .
.
После аппроксимации производных на сетке получаем:
![]() (26)
(26)
В этом случае
условия устойчивости получаются из
исследования корней так называемого
характеристического
уравнения.
Рассмотрим однородное уравнение (26) при
![]() и сделаем подстановку
и сделаем подстановку![]() →
→![]() .
После сокращения на множитель
.
После сокращения на множитель![]() ,
получаем:
,
получаем:
![]() (27)
(27)
Уравнение (27) называется характеристическим уравнением.
Сформулируем
следующий спектральный
признак
устойчивости: Для устойчивости разностной
схемы по правой части необходимо, чтобы
все корни характеристического уравнения
(27) удовлетворяли условию
![]() .
.
Пример 2. Исследуем на устойчивость метод Эйлера для модельной задачи Коши:
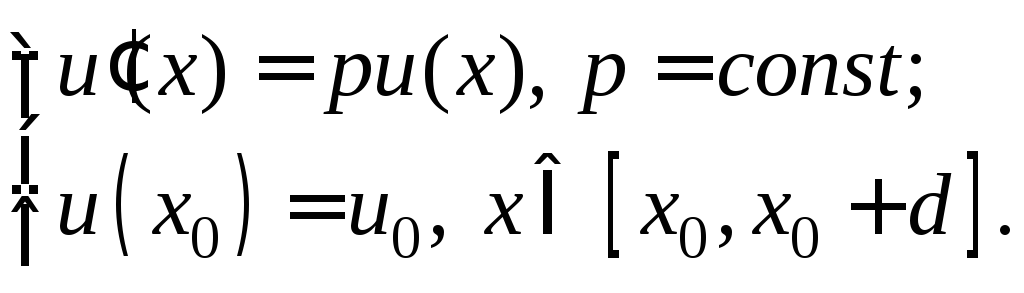 (28)
(28)
![]() Уравнение (28)
линейное и допускает точное решение
Уравнение (28)
линейное и допускает точное решение
![]() .
.
Очевидно, что при
![]() получаем экспоненциальный рост решения
получаем экспоненциальный рост решения![]() при
при![]() .
Решение задачи (28) конечно-разностным
методом Эйлера приводит к итерационной
процедуре
.
Решение задачи (28) конечно-разностным
методом Эйлера приводит к итерационной
процедуре
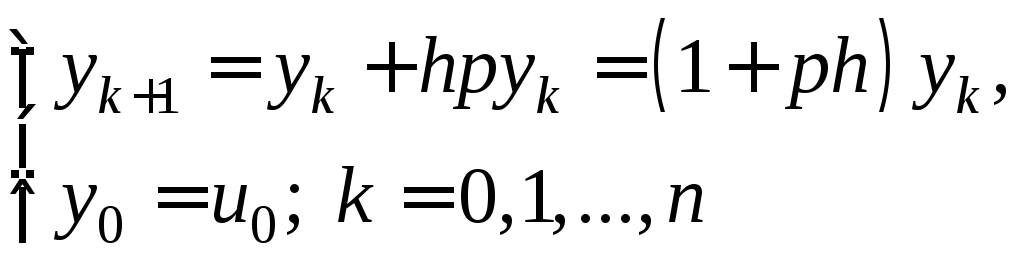
Характеристическое
уравнение имеет вид:
![]() .
Условие устойчивости для этого
единственного корня:
.
Условие устойчивости для этого
единственного корня:![]() .
Полученное неравенство выполняется,
если
.
Полученное неравенство выполняется,
если![]() Таким образом, получаем ограничение на
шаг сетки.
Таким образом, получаем ограничение на
шаг сетки.![]()
Перейдем от ОДУ к уравнениям в частных производных и рассмотрим уравнение теплопроводности
![]() (29)
(29)
в прямоугольнике
![]() .
Аппроксимируя на сетке
.
Аппроксимируя на сетке![]() производные
производные![]() и
и![]() ,
получаем конечно-разностные схемы того
или иного порядка.
,
получаем конечно-разностные схемы того
или иного порядка.
Пример 3.
Исследовать на устойчивость К.-Р. схему
порядка
![]() для уравнения (29).
для уравнения (29).
![]() Аппроксимируя
производные со вторым порядком, получаем
схему
Аппроксимируя
производные со вторым порядком, получаем
схему
![]()
где обозначено
![]() .
Характеристическое уравнение получаетсяметодом
гармоник,
т.е. подстановкой
.
Характеристическое уравнение получаетсяметодом
гармоник,
т.е. подстановкой
![]() (
(![]() -амплитуда
гармоники,
-амплитуда
гармоники,
![]() -фаза)
в однородное уравнение. После подстановки
и сокращения на общий множитель
-фаза)
в однородное уравнение. После подстановки
и сокращения на общий множитель
![]() ,
получаем:
,
получаем:
![]() .
.
Таким образом,
характеристическое уравнение приобретает
вид:
![]() ,
корни которого
,
корни которого
![]() .
.
Очевидно, что
![]() ,
поэтому полученная схема неустойчива.
,
поэтому полученная схема неустойчива.![]()
Пример 4. Исследовать
на устойчивость К.-Р. схему для уравнения
(29) порядка точности
![]() .
.
![]() Соответствующая
конечно-разностная схема имеет вид:
Соответствующая
конечно-разностная схема имеет вид:
![]()
Методом гармоник получаем характеристическое уравнение
![]() .
.
Условие устойчивости
приводит к неравенству для шагов сетки
![]()
![]()
16. Правило Рунге практической оценки погрешности квадратурной формулы Симпсона.


10. Среднеквадратичное приближение. Метод наименьших квадратов в регрессионном анализе. Вывод уравнения прямой регрессии.