41. Общая постановка краевой задачи для оду 2-го порядка. Классификация граничных условий.

Рассмотрим вначале общую нелинейную постановку краевой задачи для ОДУ второго порядка:

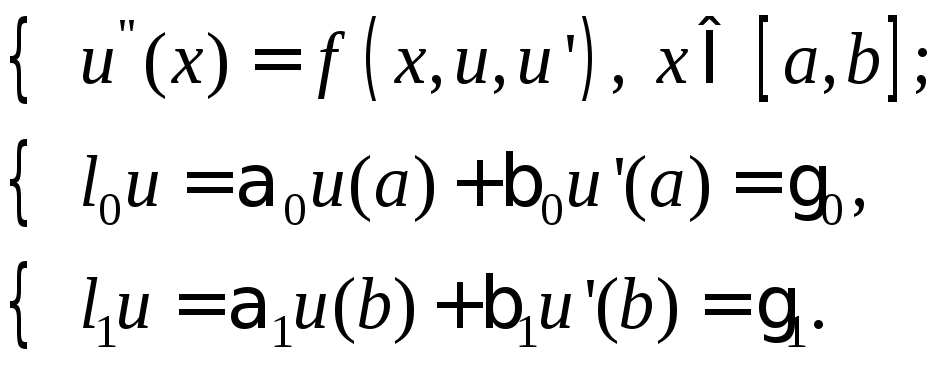(18)

В постановке задачи (18) принята следующая классификация граничных условий:

при - краевые условия –однородные; при - краевоеусловие первого рода на левом конце; при - краевое условиевторого рода на левом конце; при - краевые условиятретьего рода на левом конце. На правом конце отрезка краевые условия классифицируются аналогично.

Отметим основное отличие краевой задачи (18) от задачи Коши: в задаче Коши начальные условия задаются в одной точке (как правило, на левом конце отрезка), а в краевой задаче – на обоих концах. Естественно попытаться свести краевую задачу к задаче Коши, т.к. для нее разработаны эффективные итерационные методы решения. Таковым, например, является метод стрельбы.

42. Метод “стрельбы” решения краевой задачи с граничными условиями первого рода.

Для простоты рассмотрим задачу (18) с краевыми условиями первого рода:

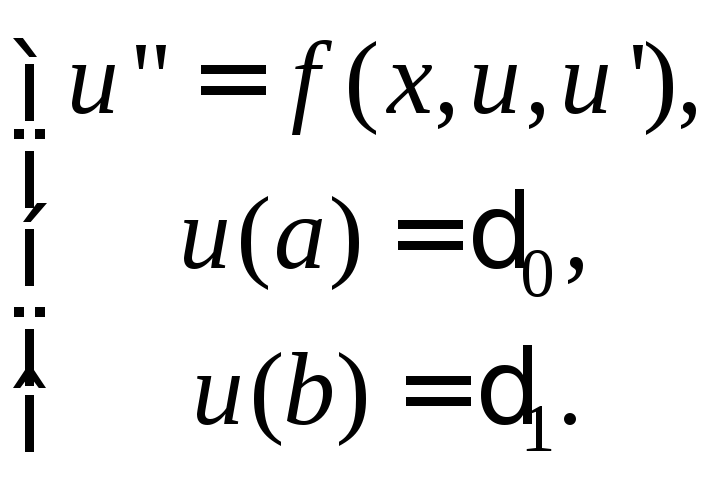(19)

Заменим задачу (19) на следующую задачу Коши:

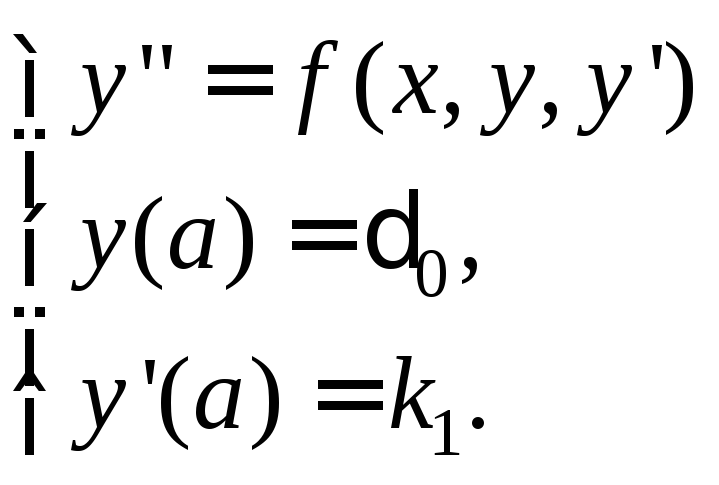(20)

Зададим какое-либо значение параметру и решим задачу (20) подходящим методом Рунге-Кутты. Обозначим полученное решениеи вычислим разность- погрешность решения на правом конце. Корректируем угловой коэффициентна левом конце в зависимости от знака погрешности, заменяя его на. Находим новое решениеи т.д. до тех пор, пока не выполнится условие, где- заданная погрешность. Название метода связано с его геометрической интерпретацией:стрельба из точки с координатами под углом, определяемым угловым коэффициентом.

43. Метод конечных разностей решения линейной краевой задачи для оду 2-го порядка.

Наиболее эффективно этот метод применяется для линейной краевой задачи, постановка которой для дифференциального уравнения второго порядка имеет вид:

(21)

Введем равномерную сетку - шаг сетки.

Определим на этой сетке сеточные функции:

, где - точное решение на сетке.

Запишем основное уравнение системы (21) для фиксированного узла :

. (22)

В каждом внутреннем узле сетки () аппроксимируем производные по формулам второго порядка точности (см. теор. 4.1 – 4.3):

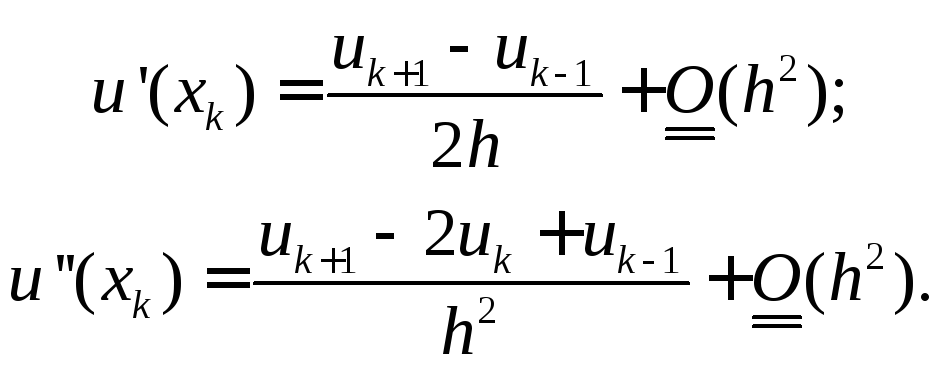
Подставим полученные соотношения в (22):

,

где обозначено -сеточный оператор, действующий на сетке. Умножая обе части уравнения на и отбрасывая остаточный член, получим приближение к точному уравнению:

.

Приводя подобные члены, получим окончательно:

,

(23)

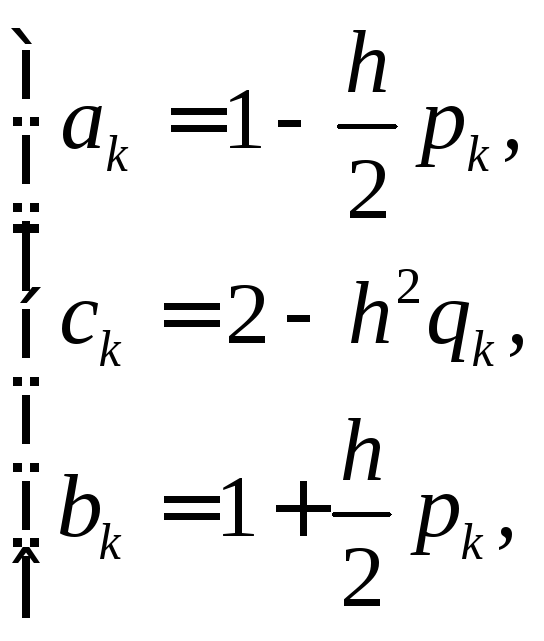
Общее число неизвестных на сетке равно (), а система (23) содержитуравнение для неизвестных. Недостающие значения должны быть определены из граничных условий. Порядок аппроксимации основного уравнения системы. При постановке задачи с краевыми условиями первого рода порядок аппроксимации всей схемы не ухудшится и будет равен. В случае краевых условий второго или третьего рода необходимо аппроксимировать их также со вторым порядком, чтобы не потерять общий второй порядок аппроксимации всей схемы. Рассмотрим один из вариантов аппроксимации краевого условия третьего рода на левом конце отрезка.

Граничное условие третьего рода имеет вид (см. урав.(18)):

(24)

Разложим функцию по Тэйлору с центром в точкеи найдем значение:

найдем из уравнения (21), аппроксимируя его в точке сетки (непрерывность вторых производных на отрезкепозволяет это сделать):

.

Подставляя найденное значение второй производной в выражение для , получаем:

.

Отбрасывая остаточный член и приводя подобные в последнем уравнении, получаем систему линейных уравнений для неизвестных :

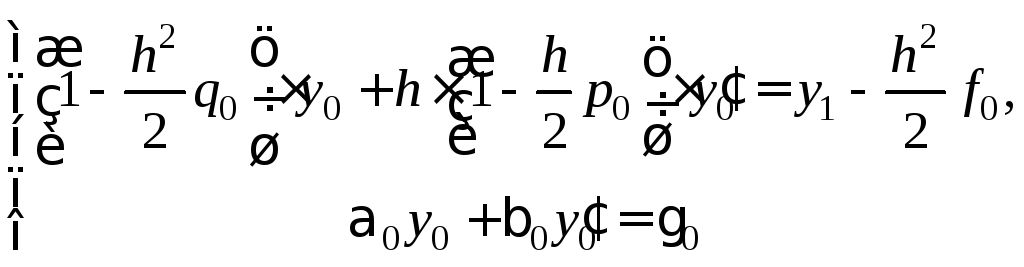
Исключая из полученной системы , получаем линейное уравнение, связывающее два сеточных значенияи:

,

где параметры легко выражаются через. Аналогично аппроксимируется третье краевое условие на правом конце отрезка, которое приводится к виду

.

В результате получаем неявную конечно-разностную систему уравнений, записанную в каноническом виде:

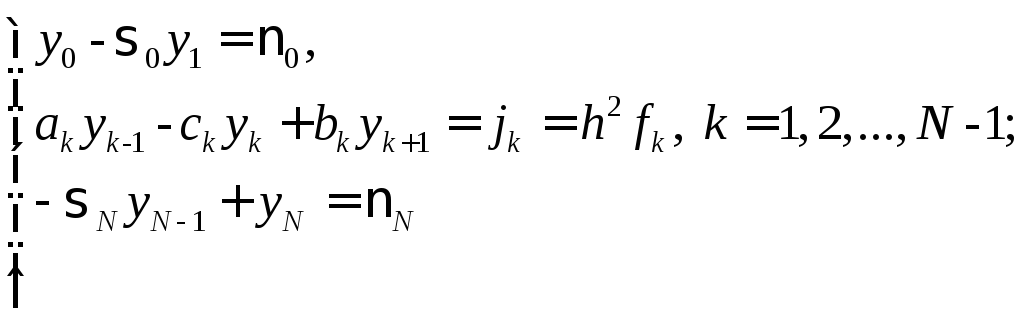(25)

Система (25) - трехдиагональная, для которой разработаны специальные эффективные методы численного решения, например, метод прогонки [1,6,11].

Исследуем вопрос о сходимости решения системы (25). Одно из условий метода Якоби (и соответственно, методов Зейделя и верхней релаксации): - очевидно выполняется. Следующее условие требует «диагонального преобладания», т.е.. Подставляя сюда значения коэффициентов системы (23), получаем:

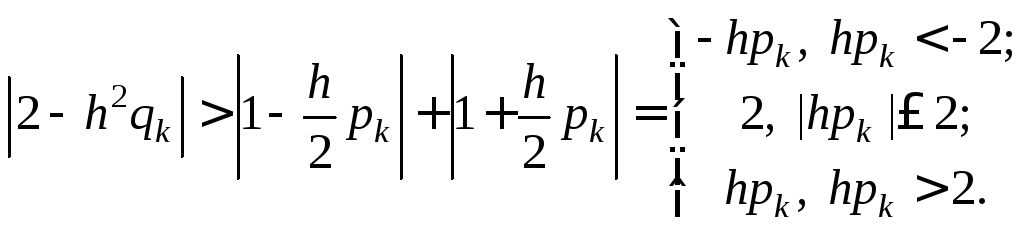
Полученное неравенство выполняется, если одновременно выполняются условия

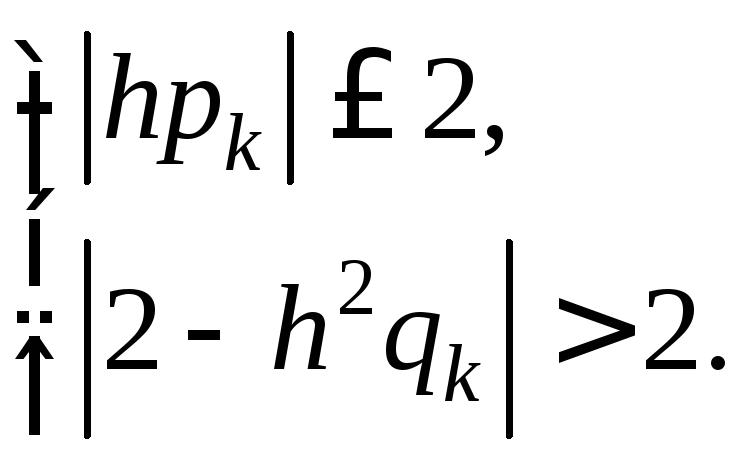
Отсюда следует, что должны выполняться условия

.

Усиливая последнее неравенство, получаем условие на шаг сетки:

.
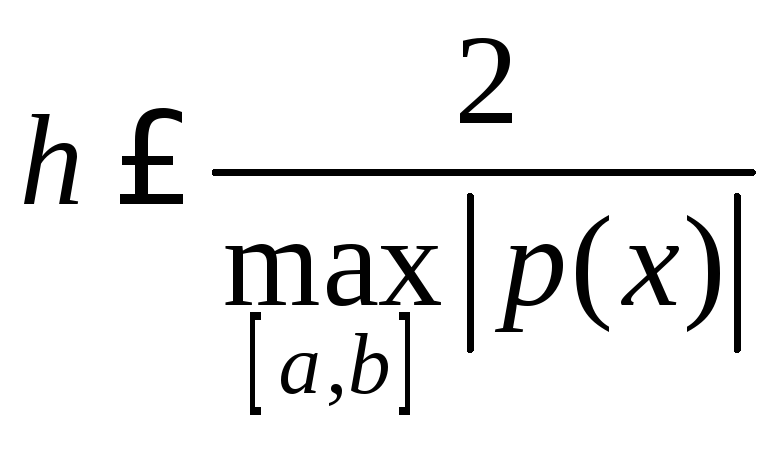