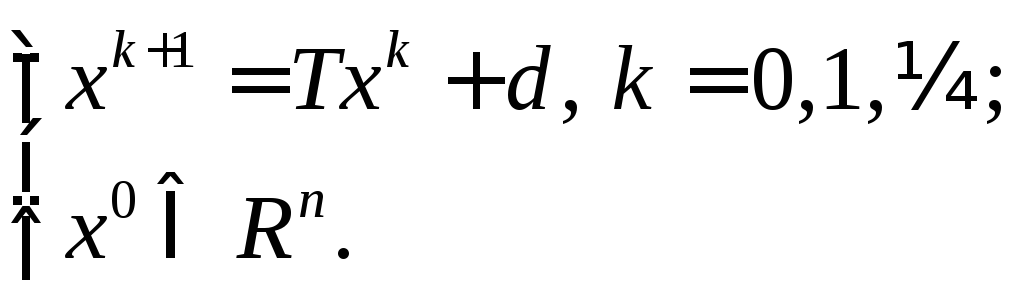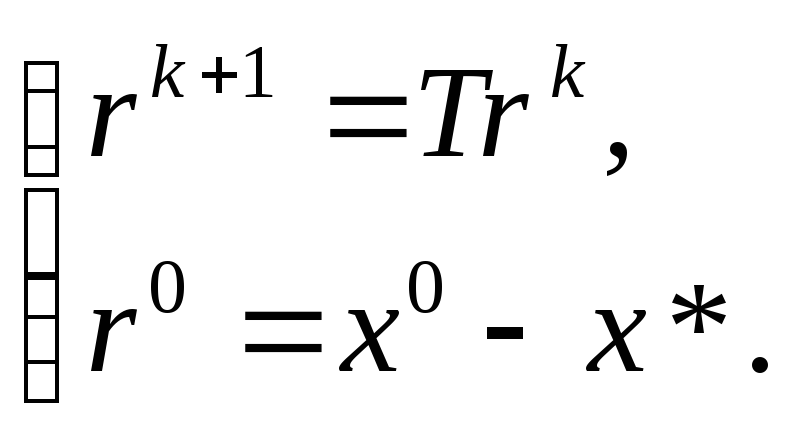- •Определение 2. Величина называется абсолютной погрешностью представления числа X с помощью числа .
- •1.2 Распространение ошибок округления в арифметических операциях.
- •1.7.2. Простейшие свойства многочленов Чебышева.
- •11. Численное интегрирование. Использование функциональных рядов.
- •12. Квадратурные формулы на основе интерполяции. Формулы для коэффициентов и остаточного члена.
- •13. Базовые квадратурные формулы прямоугольников, трапеций и парабол. Формулы теоретической погрешности.
- •14. Обобщенные квадратурные формулы трапеций и Симпсона
- •15. Теоретические оценки погрешности обобщенных формул трапеций и Симпсона.
- •17. Общие свойства полиномов ортогональных с весом.
- •18. Алгебраическая степень точности квадратурной формулы. Квадратурные формулы Гаусса-Кристоффеля.
- •19. Теорема о необходимых условиях выбора узлов в формулах Гаусса-Кристоффеля.
- •20. Классические ортогональные многочлены. Построение ортогональных многочленов Лежандра на каноническом отрезке [-1,1].
- •2. Покажем, что - неподвижная точка. Из сходимостиследует, т.Е.
- •22. Метод простых итераций решения функциональных уравнений и систем. Условия сходимости.
- •23. Метод Ньютона. Геометрическая интерпретация. Теорема о сходимости метода в одномерном случае.
- •24. Метод Ньютона в многомерном случае. Организация итерационного алгоритма.
- •25. Численные методы решения слау. Прямые и итерационные методы – общие понятия.
- •26. Нормы вещественных квадратных матриц. Спектральные свойства матриц.
- •27. Обусловленность матриц и систем лау. Определение числа обусловленности.
- •28. Метод итераций для слау второго рода. Теорема о достаточных условиях сходимости.
- •29. Спектральный признак сходимости (теорема о необх. И достат. Условиях сходимости).
- •30. Стационарные итерационные процедуры. Приведение слау первого рода к системе второго рода.
- •31. Метод простых итераций Ричардсона. Условия сходимости.
- •32. Теорема о выборе ускоряющего множителя в методе Ричардсона.
- •33. Метод Якоби. Организация алгоритма. Теорема о достаточных условиях сходимости.
- •34. Метод Зейделя как ускорение метода Якоби. Организация алгоритма. Теорема об условиях сходимости.
- •35. Метод последовательной верхней релаксации. Организация алгоритма.
- •36. Численное дифференцирование на основе интерполяции.
- •37. Численное дифференцирование на равномерной сетке, основанное на тэйлоровском разложении. Теоремы об аппроксимации первой и второй производной.
- •38. Задача Коши. Постановки задачи в одномерном случае для первой и второй производной. Сведение к системе уравнений с первой производной.
- •39. Метод Эйлера. Алгоритм, геометрическая интерпретация, порядок точности.
- •40. Методы Рунге-Кутты повышенной точности. Метод “предиктор – корректор” и метод «средней точки».
- •41. Общая постановка краевой задачи для оду 2-го порядка. Классификация граничных условий.
- •42. Метод “стрельбы” решения краевой задачи с граничными условиями первого рода.
- •43. Метод конечных разностей решения линейной краевой задачи для оду 2-го порядка.
- •45. Устойчивость разностных схем. Спектральный признак устойчивости для уравнений с постоянными коэффициентами. Примеры для оду и уравнений в частных производных.
- •16. Правило Рунге практической оценки погрешности квадратурной формулы Симпсона.
- •10. Среднеквадратичное приближение. Метод наименьших квадратов в регрессионном анализе. Вывод уравнения прямой регрессии.
27. Обусловленность матриц и систем лау. Определение числа обусловленности.
Пусть дана система
ЛАУ с невырожденной матрицей А
![]() :
:
|
Ax=b, |
(23) |
и пусть вектор
правой части b
вычисляется с ошибкой
![]() .
.
Заменим правую
часть “возмущенным” значением
![]() ,
тогда решение приобретет ошибку
,
тогда решение приобретет ошибку![]() и система примет вид:
и система примет вид:
|
|
(24) |
Оценим относительную
ошибку решения
![]() в зависимости от относительной величины
возмущения правой части
в зависимости от относительной величины
возмущения правой части![]() .
.
Из (23) и (24) следует:
![]() или
или![]() .
.
Из совокупности равенств
|
|
(25)
|
С другой стороны, из (23) следует
![]() .
.
Последнее неравенство подставим в (25)
|
|
(26) |
Определение 6.
Число
![]() называетсячислом
обусловленности
матрицы А.
называетсячислом
обусловленности
матрицы А.
Таким образом, из (26) следует, что относительная ошибка решения пропорциональна числу обусловленности матрицы А:
![]() .
.
Если
![]() (система уравненийплохо
обусловлена),
то небольшие погрешности вычисления
правой части (небольшие “возмущения”)
могут приводить к весьма большим
отклонениям от точного решения
невозмущенной системы (23).
(система уравненийплохо
обусловлена),
то небольшие погрешности вычисления
правой части (небольшие “возмущения”)
могут приводить к весьма большим
отклонениям от точного решения
невозмущенной системы (23).
Заметим, что это явление не связано с явлением неустойчивости (т.е. накоплением ошибок при вычислениях), а является следствием специфического свойства матрицы А и наблюдается даже в том случае, когда все вычисления делаются абсолютно точно, а возмущение правой части вызвано неточностями начальных данных при формировании системы
28. Метод итераций для слау второго рода. Теорема о достаточных условиях сходимости.
Рассмотрим вначале систему ЛАУ специального вида
|
x=Tx+d,
|
(27) |
Назовем эту систему системой второго рода, в отличие от вида системы (23) из параграфа 3.4.3. – системы первого рода.
Систему второго рода (27) естественно пытаться решать итерационным методом
|
|
(28) |
В этом методе используются лишь операции сложения и умножения, и не используется операция обращения матрицы – наиболее опасная для накопления ошибок.
Теорема 3.6. Для
любой согласованной матричной нормы
![]() имеет место неравенство
имеет место неравенство![]() .
.
![]() Пусть
Пусть
![]() - собственный вектор матрицы
- собственный вектор матрицы![]() ,
,![]() - соответствующее собственное значение.
Тогда справедлива следующая цепочка
равенств и неравенств:
- соответствующее собственное значение.
Тогда справедлива следующая цепочка
равенств и неравенств:
![]() ,
в силу согласованности норм. Отсюда
получаем
,
в силу согласованности норм. Отсюда
получаем
![]() .
В силу произвольности собственного
значения
.
В силу произвольности собственного
значения
![]() ,
получаем требуемый результат
,
получаем требуемый результат![]() .
.
Теорема 3.7.
(Достаточное
условие сходимости итерационной
процедуры (28)).
Пусть система
(27)
![]() невырождена, т.е. имеет единственное
решение
невырождена, т.е. имеет единственное
решение![]() ,
матрица
,
матрица![]() - вещественная, причем
- вещественная, причем![]() (в какой-либо матричной форме), тогда
итерационная процедура (28) сходится к
решению
(в какой-либо матричной форме), тогда
итерационная процедура (28) сходится к
решению![]() при
при![]() со скоростью геометрической прогрессии.
со скоростью геометрической прогрессии.
![]() .Поскольку
.Поскольку
![]() - решение системы (27), то
- решение системы (27), то![]() .
Найдем разность
.
Найдем разность
![]() .
.
Обозначим
![]() - вектор ошибкиk-ого
шага. Тогда получаем итерационную
процедуру
- вектор ошибкиk-ого
шага. Тогда получаем итерационную
процедуру
|
|
(29) |
Оператор
![]() - линейный и отображает
- линейный и отображает![]() в себя. Согласно основному принципу
сжатых отображений (теорема 3.2 для
банахова пространства): если операторT
удовлетворяет условию Липшица с
константой
в себя. Согласно основному принципу
сжатых отображений (теорема 3.2 для
банахова пространства): если операторT
удовлетворяет условию Липшица с
константой
![]()
![]()
то оператор T в уравнении (29) – сжимающий и выполняется принцип сжатых отображений.
В нашем случае имеем:
![]() .
.
Т.к.
![]() по условию
по условию![]() оператор
оператор![]() - сжимающий и, следовательно, существует
единственная неподвижная точка уравнения
- сжимающий и, следовательно, существует
единственная неподвижная точка уравнения
![]() (30)
(30)
Обозначим эту
точку
![]() .
Таким образом, выполняются уравнения:
.
Таким образом, выполняются уравнения:
![]() и, кроме того, по
определентю
и, кроме того, по
определентю
![]() .
Отсюда
.
Отсюда
![]() ,
,
Откуда получаем:
![]() .
Из единственности решения системы (27)
получаем:
.
Из единственности решения системы (27)
получаем:
![]() ,
т.е.
,
т.е.
![]() и итерационная процедура (28) сходится
к единственной неподвижной точке
и итерационная процедура (28) сходится
к единственной неподвижной точке![]() со скоростью геометрической прогрессии
со скоростью геометрической прогрессии![]() .
.

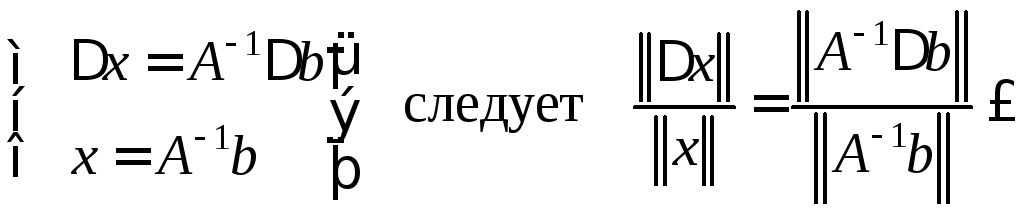 {согласованность
матриц}
{согласованность
матриц}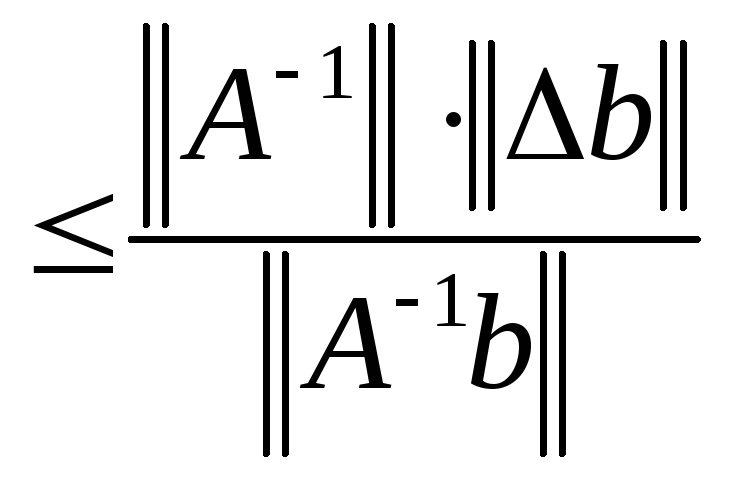 .
.