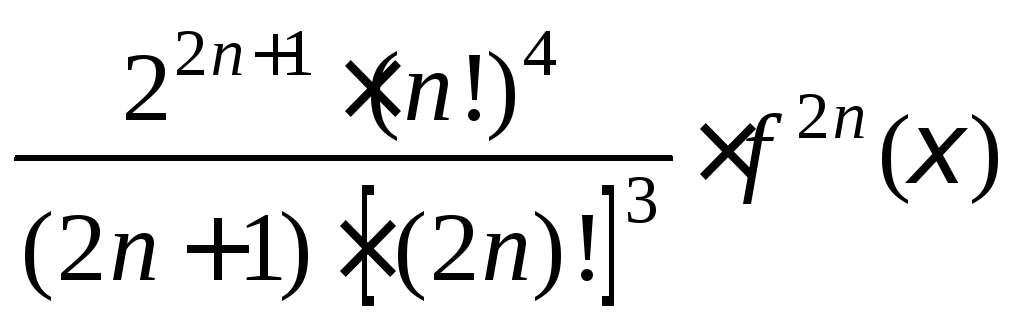- •Определение 2. Величина называется абсолютной погрешностью представления числа X с помощью числа .
- •1.2 Распространение ошибок округления в арифметических операциях.
- •1.7.2. Простейшие свойства многочленов Чебышева.
- •11. Численное интегрирование. Использование функциональных рядов.
- •12. Квадратурные формулы на основе интерполяции. Формулы для коэффициентов и остаточного члена.
- •13. Базовые квадратурные формулы прямоугольников, трапеций и парабол. Формулы теоретической погрешности.
- •14. Обобщенные квадратурные формулы трапеций и Симпсона
- •15. Теоретические оценки погрешности обобщенных формул трапеций и Симпсона.
- •17. Общие свойства полиномов ортогональных с весом.
- •18. Алгебраическая степень точности квадратурной формулы. Квадратурные формулы Гаусса-Кристоффеля.
- •19. Теорема о необходимых условиях выбора узлов в формулах Гаусса-Кристоффеля.
- •20. Классические ортогональные многочлены. Построение ортогональных многочленов Лежандра на каноническом отрезке [-1,1].
- •2. Покажем, что - неподвижная точка. Из сходимостиследует, т.Е.
- •22. Метод простых итераций решения функциональных уравнений и систем. Условия сходимости.
- •23. Метод Ньютона. Геометрическая интерпретация. Теорема о сходимости метода в одномерном случае.
- •24. Метод Ньютона в многомерном случае. Организация итерационного алгоритма.
- •25. Численные методы решения слау. Прямые и итерационные методы – общие понятия.
- •26. Нормы вещественных квадратных матриц. Спектральные свойства матриц.
- •27. Обусловленность матриц и систем лау. Определение числа обусловленности.
- •28. Метод итераций для слау второго рода. Теорема о достаточных условиях сходимости.
- •29. Спектральный признак сходимости (теорема о необх. И достат. Условиях сходимости).
- •30. Стационарные итерационные процедуры. Приведение слау первого рода к системе второго рода.
- •31. Метод простых итераций Ричардсона. Условия сходимости.
- •32. Теорема о выборе ускоряющего множителя в методе Ричардсона.
- •33. Метод Якоби. Организация алгоритма. Теорема о достаточных условиях сходимости.
- •34. Метод Зейделя как ускорение метода Якоби. Организация алгоритма. Теорема об условиях сходимости.
- •35. Метод последовательной верхней релаксации. Организация алгоритма.
- •36. Численное дифференцирование на основе интерполяции.
- •37. Численное дифференцирование на равномерной сетке, основанное на тэйлоровском разложении. Теоремы об аппроксимации первой и второй производной.
- •38. Задача Коши. Постановки задачи в одномерном случае для первой и второй производной. Сведение к системе уравнений с первой производной.
- •39. Метод Эйлера. Алгоритм, геометрическая интерпретация, порядок точности.
- •40. Методы Рунге-Кутты повышенной точности. Метод “предиктор – корректор” и метод «средней точки».
- •41. Общая постановка краевой задачи для оду 2-го порядка. Классификация граничных условий.
- •42. Метод “стрельбы” решения краевой задачи с граничными условиями первого рода.
- •43. Метод конечных разностей решения линейной краевой задачи для оду 2-го порядка.
- •45. Устойчивость разностных схем. Спектральный признак устойчивости для уравнений с постоянными коэффициентами. Примеры для оду и уравнений в частных производных.
- •16. Правило Рунге практической оценки погрешности квадратурной формулы Симпсона.
- •10. Среднеквадратичное приближение. Метод наименьших квадратов в регрессионном анализе. Вывод уравнения прямой регрессии.
20. Классические ортогональные многочлены. Построение ортогональных многочленов Лежандра на каноническом отрезке [-1,1].
Замечание 2.
Классические
ортогональные многочлены обычно строятся
для канонических промежутков:
![]() с соответствующими весами
с соответствующими весами![]() .
.
Таблица 2.1. Основные канонические системы ортогональных многочленов:
|
П Промежуток |
Весовая функция |
Название ортогональной системы |
Остаточный
член
|
|
|
|
|
Полиномы Лежандра |
|
|
|
|
|
Полиномы Чебышева |
|
|
|
|
|
Полиномы Лагерра |
Смотри в справочной литературе. | |
|
|
|
Полиномы Эрмита | ||
Самая простая
формула Гаусса-Кристоффеля имеет место
для промежутка
![]() с весом
с весом![]() (используются нули полинома Чебышева
(используются нули полинома Чебышева![]() ):
):
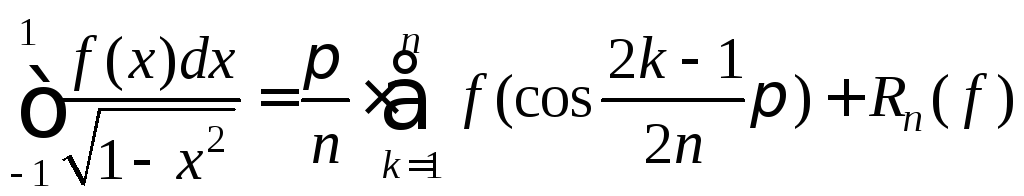 ,
,
где
![]() .
.
Пример 3. Вычисляется интеграл
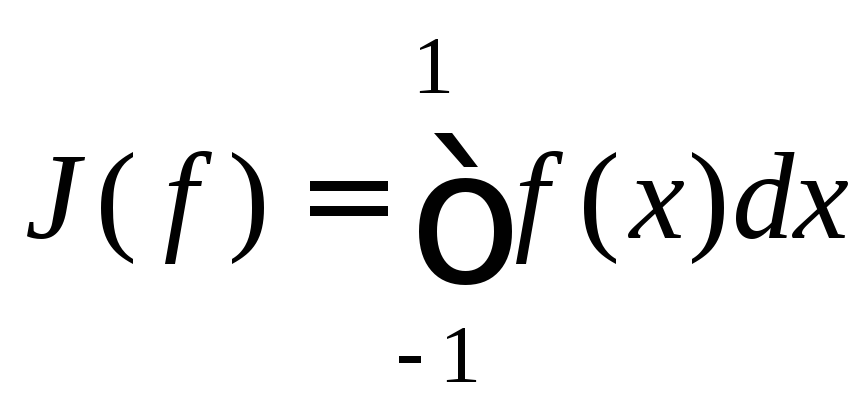
с помощью квадратурной
формулы Гаусса-Кристоффеля порядка
![]() .
Оценить по модулю
.
Оценить по модулю![]() и указать саму формулу.
и указать саму формулу.
![]()
![]() - нули многочлена
Лежандра
- нули многочлена
Лежандра
![]() (см.
пример 16 п.п. 1.8 и семинарское занятие
С-3):
(см.
пример 16 п.п. 1.8 и семинарское занятие
С-3):
![]()
![]() ,
,
![]() .
.
Найдем
нули полинома
![]() :
:![]()
![]()
![]()
![]()
![]() ,
,
![]() ,
,![]() .
.
Для вычисления
коэффициентов Кристоффеля используем
формулу для полиномов Лежандра из
таблицы 2.1. Для этого найдем сначала
значения
![]() :
:
![]() .
Подставляя найденные значения в формулу
для коэффициентов
.
Подставляя найденные значения в формулу
для коэффициентов
![]() ,
получаем:
,
получаем:![]() .
Отсюда следует формула Гаусса-Кристоффеля
3-го порядка, приближающая указанный
интеграл:
.
Отсюда следует формула Гаусса-Кристоффеля
3-го порядка, приближающая указанный
интеграл:
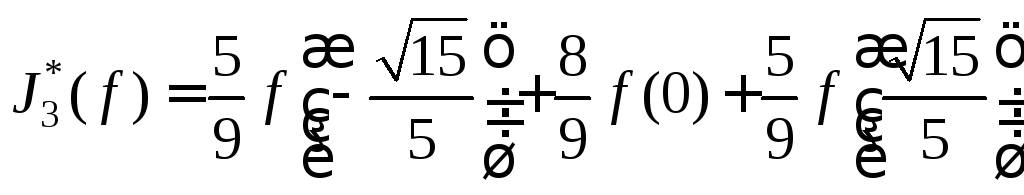 .
.
Погрешность данного
приближения вычисляем по формуле для
![]() из первой строки таб.2.1:
из первой строки таб.2.1:
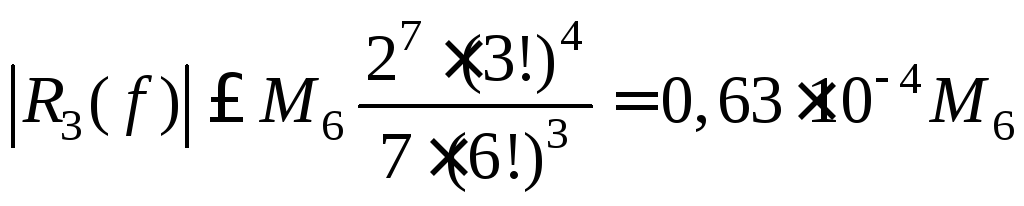 .
.
![]()
21. Принцип сжатых
отображений. Теорема о неподвижной
точке. Принципиальная схема доказательства.
Доказать единственность неподвижной
точки. Следствия теоремы для банаховых
пространств и пространства
![]() .
.
Пусть Х
– полное метрическое пространство,
![]() - расстояние между элементамих
и у.
Пусть, кроме того, S
- расстояние между элементамих
и у.
Пусть, кроме того, S![]() X
– замкнутое ограниченное множество
(компакт): и Т
– оператор (вообще говоря, – нелинейный),
действующий из S
в S,
то есть отображающий множество S
в себя:
X
– замкнутое ограниченное множество
(компакт): и Т
– оператор (вообще говоря, – нелинейный),
действующий из S
в S,
то есть отображающий множество S
в себя:
![]() .
.
Назовем точку
![]() неподвижной
точкой
оператора Т,
если
неподвижной
точкой
оператора Т,
если
|
х*=Тх* |
|
Таким образом, неподвижные точки оператора Т являются решениями уравнения
![]() (1)
(1)
Элемент
![]() называетсяобразом
элемента
называетсяобразом
элемента
![]() ,
а элемент
,
а элемент![]() ─прообразом
элемента
─прообразом
элемента
![]() .
.
Наиболее простой способ решения этого уравнения – итерационный, начиная с некоторого значения х0
|
хn+1=Txn
, х0
|
(2) |
При этом важно, чтобы такая последовательность {xn} сходилась к единственной точке х*.
Следующая теорема формулирует достаточные условия сходимости итерационного процесса.
Теорема 3.1.
(Принцип
сжатых отображений).
Пусть
Т – оператор
сжатия на
S,
то есть для любых двух точек
![]() выполняются следующие два условия
выполняются следующие два условия
1)
![]() и 2)
и 2)![]() . (3)
. (3)
Тогда в S
существует единственная неподвижная
точка оператора Т,
являющаяся пределом последовательности
{xn},
определяемой процедурой итераций (2),
начиная с
![]() .
При этом скорость сходимости оценивается
неравенствами:
.
При этом скорость сходимости оценивается
неравенствами:
|
|
(4) |
|
|
(5) |
![]() Доказательство
разобьем на несколько этапов.
Доказательство
разобьем на несколько этапов.
1. Докажем, что последовательность {xn} – фундаментальная. Рассмотрим
|
|
(6) |
Далее при p![]() 1
имеем
1
имеем
![]() {
вставим точку
{
вставим точку
![]() и воспользумся неравенством треугольника}
и воспользумся неравенством треугольника}![]()
![]() {продолжаем
вставлять точки}
{продолжаем
вставлять точки}![]()
![]() {на
основании (6)}
{на
основании (6)}![]()
![]()
![]()
|
|
(7) |
О![]() тсюда
следует, что
тсюда
следует, что![]() ,
,![]() ,
,
следовательно,
последовательность {xn}
– фундаментальная,
и согласно критерию Коши-Вейерштрасса
последовательность {xn}
сходится к
некоторому элементу
![]() (так
как S - компакт).
(так
как S - компакт).