12. Квадратурные формулы на основе интерполяции. Формулы для коэффициентов и остаточного члена.

Пусть задана сетка узлов , не обязательно равномерная. Требуется приближенно вычислить интеграл. Представим подынтегральную функциюинтерполяционным полиномом Лагранжа по данной системе узлов:, тогда

,

где

- приближенное значение интеграла,

- ошибка приближения.

Используя представление полинома Лагранжа через фундаментальные полиномы

,

получим:

,

(1)

где

.

Формула (1) называется квадратурной формулой n-го порядка. Если , то используя формулупогрешности интерполяции в точке, получим следующее выражение для погрешности квадратурной формулы:

(2)

Оценивая обе части (2) по модулю, получим оценку абсолютной погрешности

,

(3)

где

,

Стандартные квадратурные формулы получаются для равномерной сетки .

Воспользуемся первой интерполяционной формулой Ньютона:

,

(4)

где

.

В этом случае квадратурная формула n-го порядка получается при подстановке представления (4) в интеграл

и представления конечных разностей в виде линейной комбинации узловых значений функции(согласно свойству конечных разностей).

Для ошибки квадратурной формулы n-го порядка соответственно получаем выражение:

.

(5)

После замены переменной , окончательно получаем:

.

(5)

Условие связано с тем, что припонятие «шага» сетки не определено.

13. Базовые квадратурные формулы прямоугольников, трапеций и парабол. Формулы теоретической погрешности.

Перейдем к непосредственному выводу квадратурных формул для порядков .

. Пусть .

Как говорилось выше, шаг h в этом случае не определен, т.к. имеется всего один узел . Этот узел может быть выбран многими способами.

Положим, например,

(тем самым оптимизируется погрешность «в среднем» для большого семейства функций). Учитывая, что полином Ньютона нулевого порядка имеет вид

,

Получаем квадратурную формулу «нулевого порядка»

.

(6)

Формула (6) имеет простой геометрический смысл и называется «формулой прямоугольника».

Для оценки погрешности данной квадратурной формулы (как говорилось выше, при формула (6) не применима) введем «псевдошаг», положив

, и рассмотрим интеграл

. (7)

После замены переменных получим:

. (8)

Пусть . Разложим подинтегральную функцию в (8) в ряд Тэйлора до членов второго порядка:, где, и подставим в (8):

=.

Из последней формулы усматриваем, что

- приближенное значение интеграла (квадратурная формула прямоугольника);

- теоретическая погрешность формулы прямоугольника.

Из последней формулы получаем оценку абсолютной погрешности формулы прямоугольника:

.

. Используем два узла: .

и линейное приближение интерполяции:

,

. Отсюда получаем приближенное значение интеграла

-

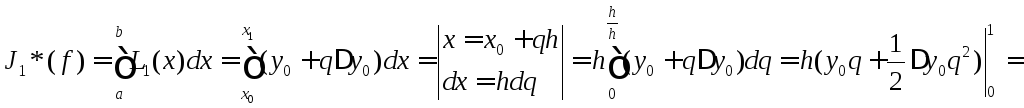
(9)

Квадратурная фомула (9) называется формулой трапеции.

Дадим геометрическую иллюстрацию формулы (9). На рисунке заштрихована площадь трапеции, определяемая формулой (9).

Погрешность формулы трапеций находим по формуле (5) (попрежнему считаем, что ):

.

(10) (10)

Из формулы (10) следует оценка абсолютной погрешности: .

. (Параболическая интерполяция). Определяем узлы: ,.

Интерполяционный полином Ньютона второго порядка имеет вид

, .

Вычисляемм приближенное значение интеграла:

.

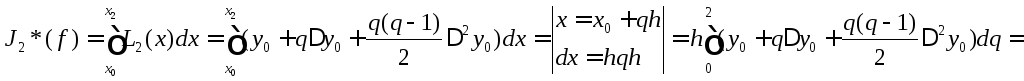
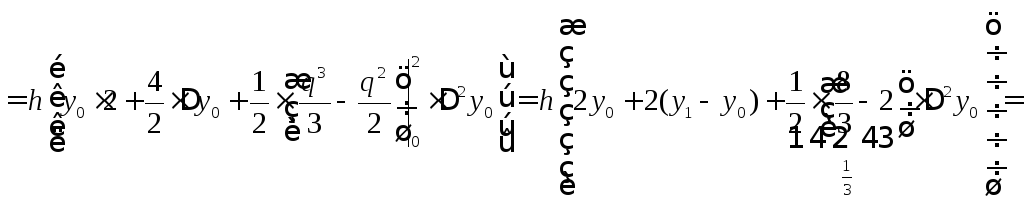
Таким образом, квадратурная формула второго порядка имеет вид

-

(11) (11)

Формула (11) носит название - формула Симпсона.

Погрешность квадратурной формулы Симпсона приведем без вывода:

.

(12) (12)

Из (12) получаем оценку абсолютной погрешности

.

Формулы (5), (10) и (12) для погрешности квадратурных формул носят теоретический характер. В частности, они позволяют выяснить, какова алгебраическая степень точности данной квадратурной формулы.

Определение. Говорят, что данная квадратурная формула имеет алгебраическую степень точности , если она точна для многочленов степени равной или меньшейs.

Из определения следует, что квадратурные формулы прямоугольников и трапеций точны для многочленов степени s=1 (т.к. для такого многочлена иза счет производной). – (См. формулы (5) и (10)).

Подобным образом убеждаемся, что формула Симпсона (11) имеет алгебраическую степень точности s=3 (следует из вида в формуле (12)). Но как видно из тех же формул дляи, точность определяется не только производной, но и шагом интерполяцииh.
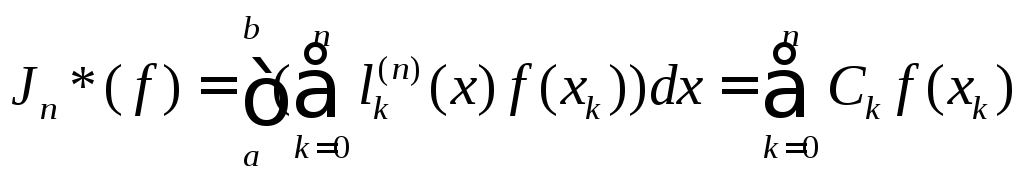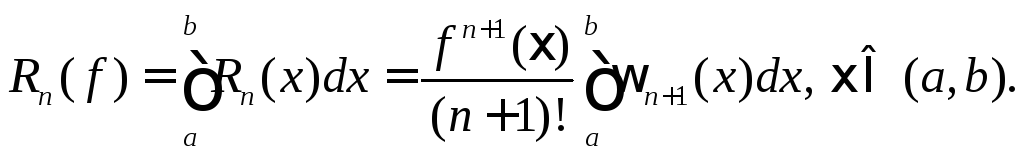
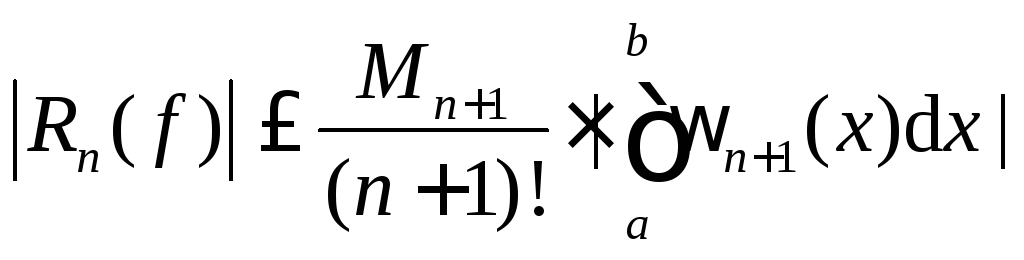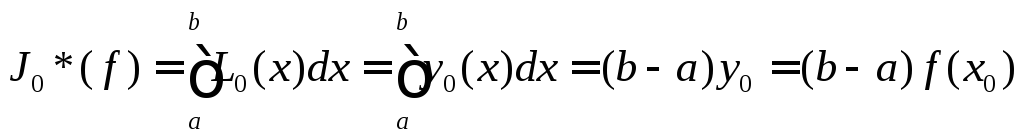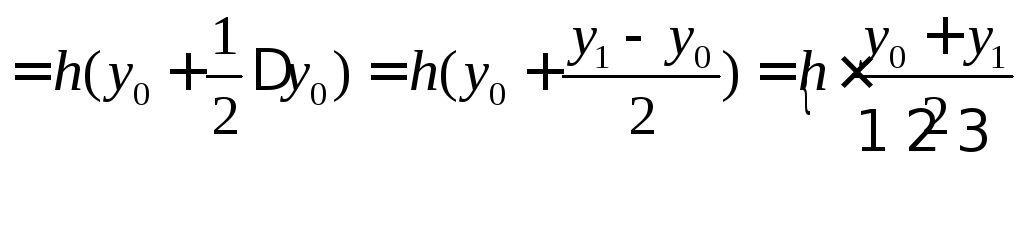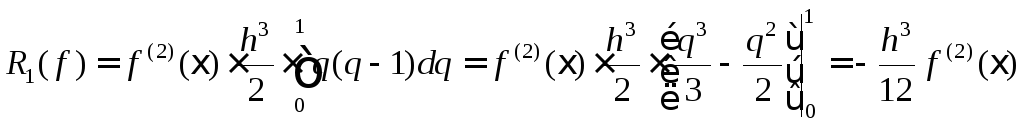