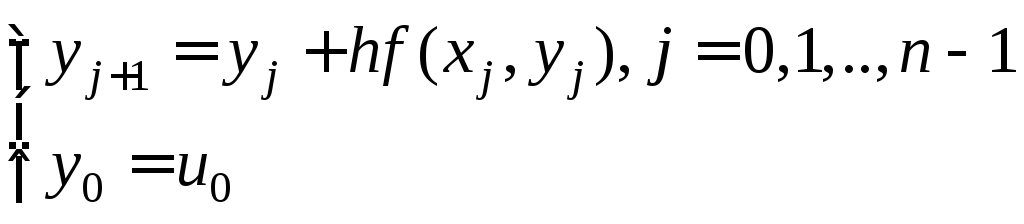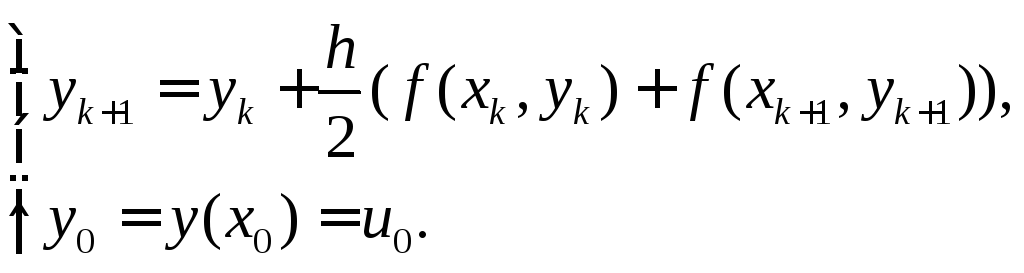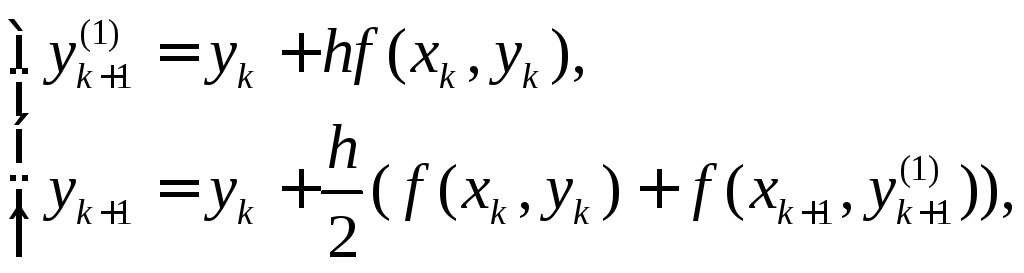- •Определение 2. Величина называется абсолютной погрешностью представления числа X с помощью числа .
- •1.2 Распространение ошибок округления в арифметических операциях.
- •1.7.2. Простейшие свойства многочленов Чебышева.
- •11. Численное интегрирование. Использование функциональных рядов.
- •12. Квадратурные формулы на основе интерполяции. Формулы для коэффициентов и остаточного члена.
- •13. Базовые квадратурные формулы прямоугольников, трапеций и парабол. Формулы теоретической погрешности.
- •14. Обобщенные квадратурные формулы трапеций и Симпсона
- •15. Теоретические оценки погрешности обобщенных формул трапеций и Симпсона.
- •17. Общие свойства полиномов ортогональных с весом.
- •18. Алгебраическая степень точности квадратурной формулы. Квадратурные формулы Гаусса-Кристоффеля.
- •19. Теорема о необходимых условиях выбора узлов в формулах Гаусса-Кристоффеля.
- •20. Классические ортогональные многочлены. Построение ортогональных многочленов Лежандра на каноническом отрезке [-1,1].
- •2. Покажем, что - неподвижная точка. Из сходимостиследует, т.Е.
- •22. Метод простых итераций решения функциональных уравнений и систем. Условия сходимости.
- •23. Метод Ньютона. Геометрическая интерпретация. Теорема о сходимости метода в одномерном случае.
- •24. Метод Ньютона в многомерном случае. Организация итерационного алгоритма.
- •25. Численные методы решения слау. Прямые и итерационные методы – общие понятия.
- •26. Нормы вещественных квадратных матриц. Спектральные свойства матриц.
- •27. Обусловленность матриц и систем лау. Определение числа обусловленности.
- •28. Метод итераций для слау второго рода. Теорема о достаточных условиях сходимости.
- •29. Спектральный признак сходимости (теорема о необх. И достат. Условиях сходимости).
- •30. Стационарные итерационные процедуры. Приведение слау первого рода к системе второго рода.
- •31. Метод простых итераций Ричардсона. Условия сходимости.
- •32. Теорема о выборе ускоряющего множителя в методе Ричардсона.
- •33. Метод Якоби. Организация алгоритма. Теорема о достаточных условиях сходимости.
- •34. Метод Зейделя как ускорение метода Якоби. Организация алгоритма. Теорема об условиях сходимости.
- •35. Метод последовательной верхней релаксации. Организация алгоритма.
- •36. Численное дифференцирование на основе интерполяции.
- •37. Численное дифференцирование на равномерной сетке, основанное на тэйлоровском разложении. Теоремы об аппроксимации первой и второй производной.
- •38. Задача Коши. Постановки задачи в одномерном случае для первой и второй производной. Сведение к системе уравнений с первой производной.
- •39. Метод Эйлера. Алгоритм, геометрическая интерпретация, порядок точности.
- •40. Методы Рунге-Кутты повышенной точности. Метод “предиктор – корректор” и метод «средней точки».
- •41. Общая постановка краевой задачи для оду 2-го порядка. Классификация граничных условий.
- •42. Метод “стрельбы” решения краевой задачи с граничными условиями первого рода.
- •43. Метод конечных разностей решения линейной краевой задачи для оду 2-го порядка.
- •45. Устойчивость разностных схем. Спектральный признак устойчивости для уравнений с постоянными коэффициентами. Примеры для оду и уравнений в частных производных.
- •16. Правило Рунге практической оценки погрешности квадратурной формулы Симпсона.
- •10. Среднеквадратичное приближение. Метод наименьших квадратов в регрессионном анализе. Вывод уравнения прямой регрессии.
39. Метод Эйлера. Алгоритм, геометрическая интерпретация, порядок точности.
Будем искать
решение задачи (6) в прямоугольнике![]() .
.
Введем равномерную
сетку на оси
![]()
![]() ,
,
![]() ,
,![]() .
.
Простейший
итерационный процесс решения задачи
(6) получается, если аппроксимировать
производную
![]() на сетке
на сетке![]() правой конечной разностью.
правой конечной разностью.
![]()
Обозначая
приближенное решение на сетке
![]() ,
и отбрасывая остаточный член, получим
,
и отбрасывая остаточный член, получим
|
|
(10) (10)
|
И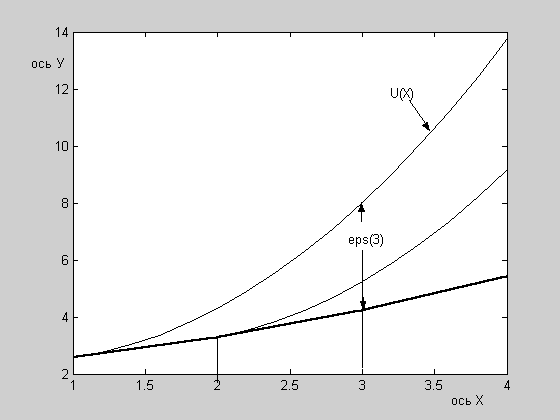 терационная
процедура (10) представляет собойметод
Эйлера (или
метод ломаных).
Графическая иллюстрация метода приведена
на рис. 4.1
терационная
процедура (10) представляет собойметод
Эйлера (или
метод ломаных).
Графическая иллюстрация метода приведена
на рис. 4.1
Рис. 4.1. Графическая иллюстрация метода Эйлера (метод ломаных). Жирная кривая – ломаная Эйлера;
U(x) – интегральная кривая, проходящая через начальную точку (1,U(1));
шаг сетки h= 1.eps(3) – погрешность в точкеx2= 3.
Начав движение из
точки
![]() на точном решении
на точном решении![]() ,
итерационное решение образует ломаную
линию, каждый отрезок которой представляет
собой касательную к кривой
,
итерационное решение образует ломаную
линию, каждый отрезок которой представляет
собой касательную к кривой![]() ,
проходящую через данную точку.
,
проходящую через данную точку.
Действительно,
запишем уравнение касательной к u(x)
в точке
![]() и положим
и положим![]() :
:
![]() .
.
Далее, аналогичным
образом, строим касательную в точке
![]() и положим
и положим![]()
![]() и т.д.
и т.д.
Здесь
![]() –
та интегральная кривая, которая проходит
через точку (x1,y1).
–
та интегральная кривая, которая проходит
через точку (x1,y1).
Из рисунка видно,
что ошибка
![]() растет с номером k.
Выясним, каков порядок этой ошибки в
сеточной норме
растет с номером k.
Выясним, каков порядок этой ошибки в
сеточной норме
![]() .
.
Будем считать, что
ошибка округления имеет порядок не
меньший, чем
![]() .
Тогда из (10) следует:
.
Тогда из (10) следует:
|
|
(11) |
Разложим точное
решение
![]() в точке
в точке![]() с такой же точностью:
с такой же точностью:
|
|
(12) |
Вычтем(12) из (11)
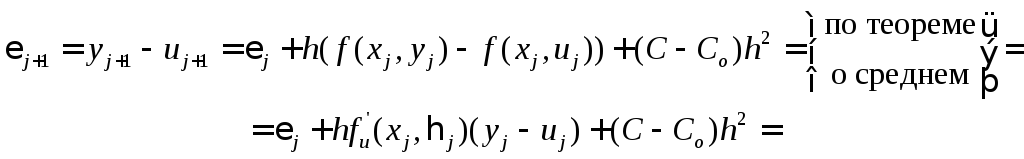
|
|
(13) |
где
![]() .
.
В силу условий
теоремы существования и единственности
частные производные
![]() ограничены в прямоугольнике
ограничены в прямоугольнике![]() :
:![]() .
.
Обозначим
![]() и оценим (13) по модулю
и оценим (13) по модулю
|
|
![]() по условию.
по условию.
Обозначим
|
|
(10) (14) |
Теорема 4.4. Для метода Эйлера имеет место следующая оценка погрешности:
|
|
(11) (15) |
![]() Из (14) следует
(используем рекурсию «назад»):
Из (14) следует
(используем рекурсию «назад»):

Используя алгебраическое тождество
![]()
получаем:
|
|
(12) |
В последнем неравенстве использован второй замечательный предел.
Учитывая, что
![]()
получаем
![]() ,
,
т.е. оценку (15).
![]()
Замечание. Из соотношений (14) и (15) следует, что
1. Ошибка растет с номером шага k.
2. Порядок ошибки
в методе Эйлера
![]() .
.
40. Методы Рунге-Кутты повышенной точности. Метод “предиктор – корректор” и метод «средней точки».
Метод
предиктор-корректор.
Проинтегрируем
обе части уравнения (6) по отрезку
![]() на равномерной сетке
на равномерной сетке![]() :
:
![]() .
.
Левую часть полученного уравнения вычисляем по формуле Лейбница:
![]() .
.
Для вычисления правой части используем квадратурную формулу трапеций:
![]()
где
![]() погрешность,
определяемая формулой
погрешность,
определяемая формулой
![]() .
.
Если отбросить остаточный член, то получаем неявную итерационную схему.
|
|
(13) (16) |
Аналогично тому,
как оценивается ошибка в методе Эйлера,
можно показать, что результирующая
ошибка метода (16) имеет порядок
![]() (теряется один порядок при приближении
к концу отрезка).
(теряется один порядок при приближении
к концу отрезка).
Т.к. схема (16)
неявная, то ее следует решать методом
итераций для фиксированных точек
![]() и
и![]() .
Более простой путь заключается в
следующем. Используем в (16) только 2
последовательных этапа итераций:
.
Более простой путь заключается в
следующем. Используем в (16) только 2
последовательных этапа итераций:
|
|
(14) (17) |
с начальным
условием: ![]() .
.
Полученная схема
(17) имеет также порядок точности
![]() и носит название «метод
предиктор-корректор»
.
и носит название «метод
предиктор-корректор»
.
Поясним геометрический смысл названия.
На первом этапе
предсказывается
значение
![]() по методу Эйлера. На втором этапе это
значениекорректируется
путем усреднения угловых коэффицинтов
в точках
по методу Эйлера. На втором этапе это
значениекорректируется
путем усреднения угловых коэффицинтов
в точках
![]() и
и![]() .
За счет коррекции точность метода и
повышается на порядок по сравнению с
методом Эйлера.
.
За счет коррекции точность метода и
повышается на порядок по сравнению с
методом Эйлера.
Метод средней
точки.
Найдем
сначала значение
![]() в промежуточной точке
в промежуточной точке![]() отрезка
отрезка![]() по простому методу Эйлера.:
по простому методу Эйлера.:
![]() - обозначим так
найденное значение
- обозначим так
найденное значение
![]() на половинном шаге от точки
на половинном шаге от точки![]() .
Затем в полученной точке
.
Затем в полученной точке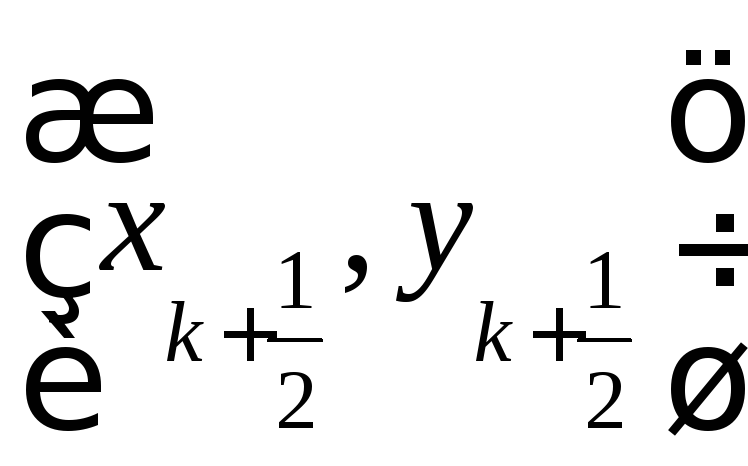 вычислим угловой коэффициент касательной
вычислим угловой коэффициент касательной и в этом направлении совершим движение
из точки
и в этом направлении совершим движение
из точки![]() в точку
в точку![]() по методу Эйлера:
по методу Эйлера:
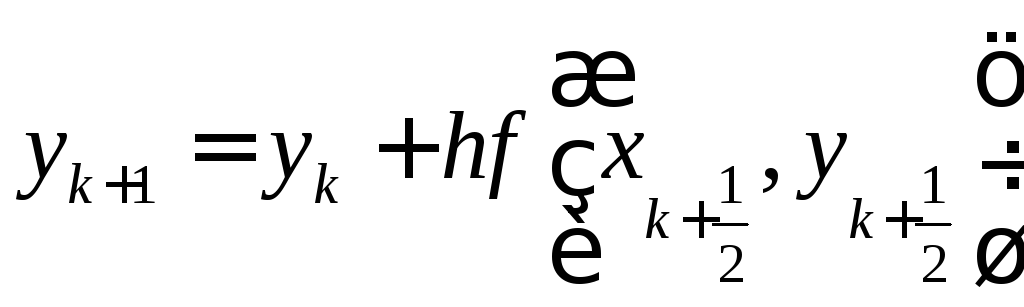 .
.
Полученный метод имеет 2-ой порядок точности и называется модифицированным методом Эйлера с коррекцией углового коэффициента на половинном шаге или более коротко─метод средней точки.
Существует общий
теоретический подход к построению явных
итерационных методов решения задачи
Коши повышенного порядка точности
![]() .
Это так называемыеМетоды
Рунге-Кутты
.
Это так называемыеМетоды
Рунге-Кутты
![]() -го
порядка, удовлетворяющие следующим
условиям.
-го
порядка, удовлетворяющие следующим
условиям.
1. Это одношаговые
методы, т.е. при переходе из точки
![]() в точку
в точку![]() используется лишь информация о предыдущей
точке
используется лишь информация о предыдущей
точке![]() .
.
2. Процедура
согласуется с рядом Тейлора вплоть до
членов порядка
![]() ,
где
,
где![]() - порядок метода.
- порядок метода.
3. Метод не использует
производных от
![]() ,
а требует только вычисления функции в
различных точках сетки, причем число
вычислений функции - минимально возможное
для данного порядка.
,
а требует только вычисления функции в
различных точках сетки, причем число
вычислений функции - минимально возможное
для данного порядка.
Заметим, что метод Эйлера является частным случаем метода Рунге-Кутты, имеющий наименьший первый порядок точности, а методы средней точки и предиктор-клрректор - методы Рунге-Кутты второго порядка.