33. Метод Якоби. Организация алгоритма. Теорема о достаточных условиях сходимости.

3. Метод Якоби.

В этом методе приведение системы (23) к виду (27) осуществляется с помощью представления матрицы А в виде:

,

(34)

где

-

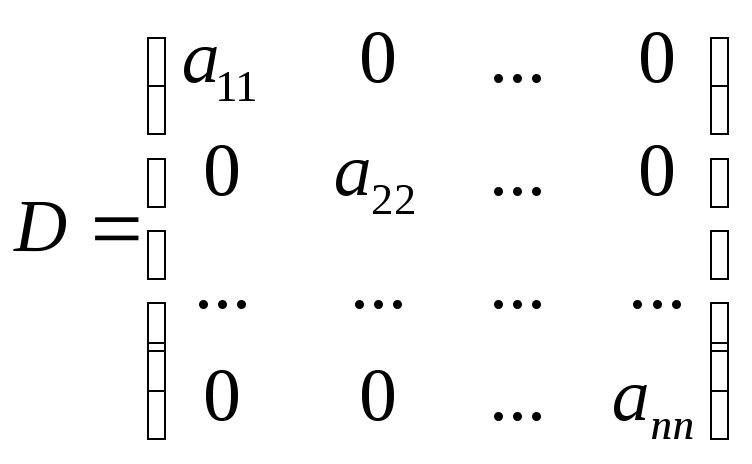- диагональная матрица,

-

- строго нижняя (lower) треугольная матрица,

-

- строго верхняя (upper) треугольная матрица.

Подставляя представление (34) в систему (23) Ax=b, получаем:

Dx=(C_L+C_U)x+b,

откуда следует

,

где матрица перехода имеет вид:

,

, – матрица расщепления.

Получаемый при этом итерационный метод называется методом Якоби. Необходимое условие сходимости: (иначе не существует ).

Достаточные условия сходимости устанавливаются в следующей теореме:

Теорема 3.10. (О сходимости метода Якоби). Пусть матрица - вещественная и удовлетворяет условиям:

.
.	(35)

(Условия (35) называются условиями строгого диагонального преобладания). Тогда метод Якоби сходится.

Условие (35) можно записать в виде:

,

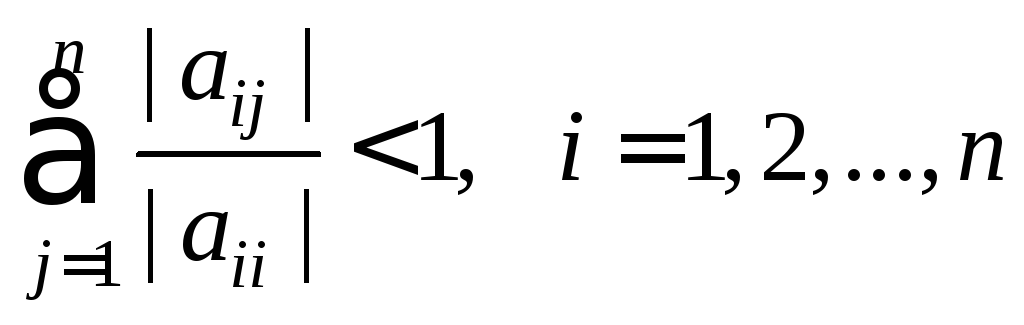что эквивалентно условию

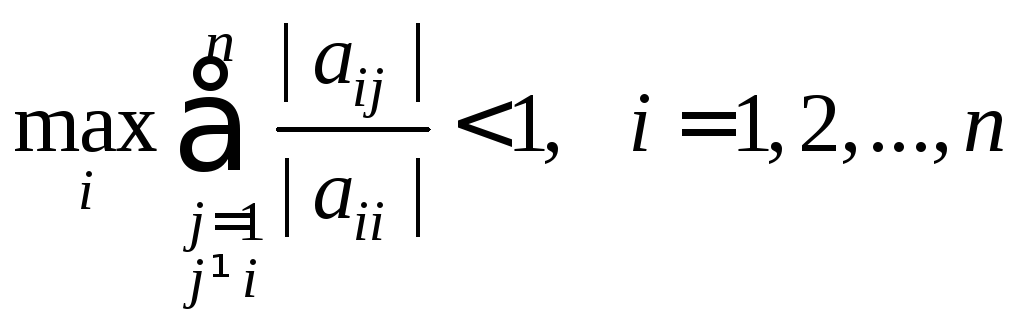. (36)

Поскольку

,

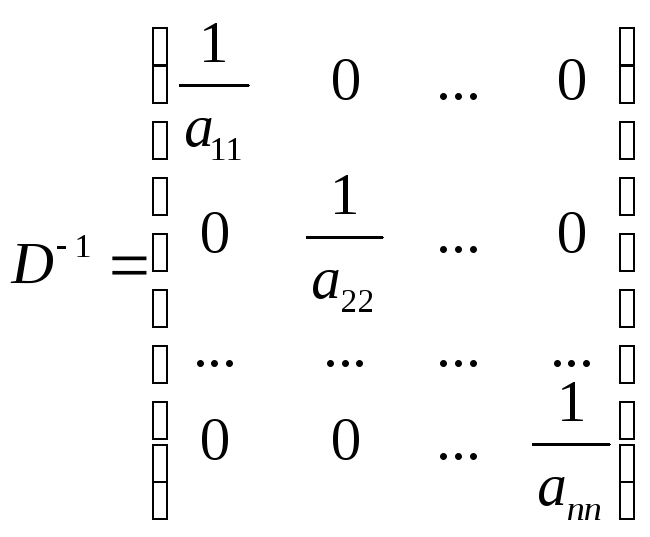то матрица перехода приобретает вид:

.

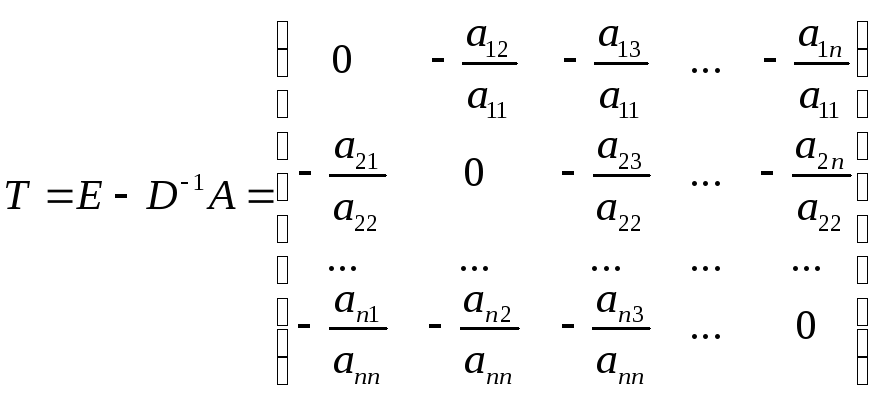Воспользуемся строчной нормой матрицы . Согласно (36):

,

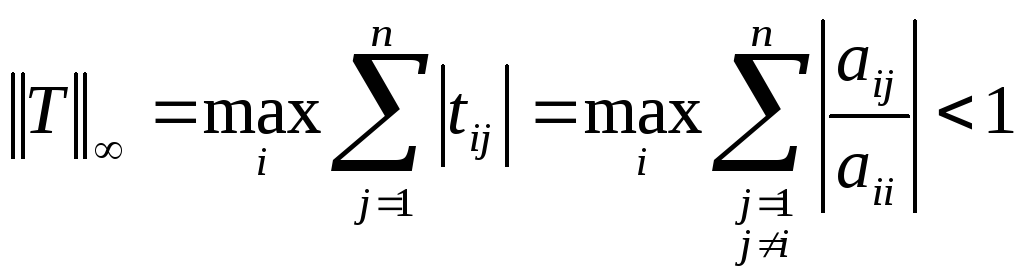и, таким образом, выполняется условие сжатости для данной нормы. Следовательно, метод Якоби сходится в строчной норме. Но поскольку. в все согласованные матричные нормы эквивалентны, то метод Якоби сходится.

Замечание. Достаточным условием сходимости метода Якоби является также спектральное условие: .

34. Метод Зейделя как ускорение метода Якоби. Организация алгоритма. Теорема об условиях сходимости.

4. Метод Зейделя (Гаусса-Зейделя).

Метод Якоби может быть оптимизирован следующим образом. Как и в методе Якоби воспользуемся разложением матрицы

,

и запишем систему в виде:

, .

(11) (37)

Обозначим

и подставим в (37):

.

(12) (38)

Нетрудно убедиться, что при покомпонентной записи уравнения (38):

вектор содержит только первые (i-1) компоненты вектора х, а вектор - содержит компоненты, начиная с (x_i+1). Таким образом, система (38) записывается в виде:

(13) (39)

При реализации метода последовательных приближений для решения системы (39) естественно использовать в правой части уже найденные значения компонент , полученные в текущей итерации.Алгоритм Гаусса-Зейделя строится следующим образом:

.

(14) (40)

Условия сходимости метода Гаусса-Зейделя (40) определяются в следующей теореме.

Теорема 3.11. Пусть выполнено условие

.

Тогда метод Гаусса-Зейделя сходится при любом выборе начального приближения и справедлива следующая оценка погрешности:

,

где .

Заметим, что так как , - топо условию. Отсюда следует, что оператор- сжимающий и итерационная процедура Зейделя (40) сходится. Для точного решения справедливо уравнение

. (41)

Кроме того, согласно процедуре Зейделя,

. (42)

Вычтем (41) из (42) и оценим по норме

.

Отсюда, приводя подобные члены, получаем неравенство

(43)

Поскольку из условия теоремы следует, что , то неравенство (43) свидетельствует о сходимости процедуры со скоростью геометрической прогрессии.

Замечание. Нетрудно убедиться, что , поэтому метод Зейделя сходится быстрее, чем метод Якоби.
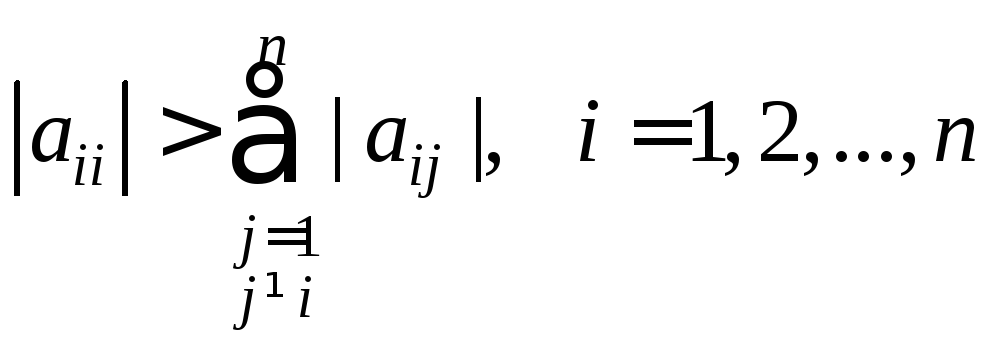