26. Нормы вещественных квадратных матриц. Спектральные свойства матриц.

Пусть - вектор-столбец,. Приведем некоторые известные нормы векторов:

1. - эклидова норма вектора;

2. 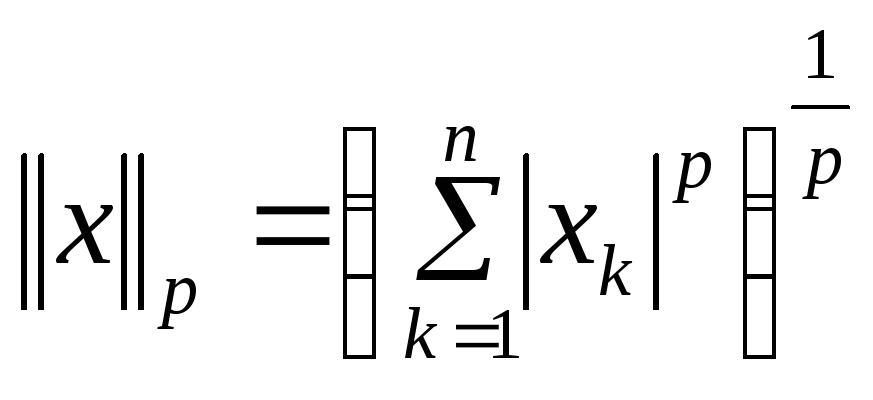- так называемая-норма, или норма Гильберта-Шмидта (при совпадает с эвклидовой нормой, а присовпадает с так называемой 1-нормой).

3. -чебышевская норма.

Все эти нормы в эквивалентны: сходимость в одной из этих норм влечет за собой сходимость в другой (следствие конечности).

Перейдем к понятию матричной нормы. Пусть - множество квадратных вещественных матриц порядка. Пусть каждой матрицепоставлено в соответствие число. Это число называетсянормой матрицы A, если выполняются следующие аксиомы:

1. ;

2. ;

3. - неравенство треугольника;

4. - кольцевое свойство.

Определение 1. Норма называетсямультипликативной, если выполняются все четыре аксиомы, и аддитивной, если выполняются только первые три аксиомы.

Определение 2. Если матричная норма удовлетворяет условию

, где ,

(1)

то такая норма называется согласованной с нормой вектора.

Большинство используемых в численном анализе матричных норм согласованы с той или иной векторной нормой.

Определим некоторые наиболее употребительные на практике матричные нормы.

-

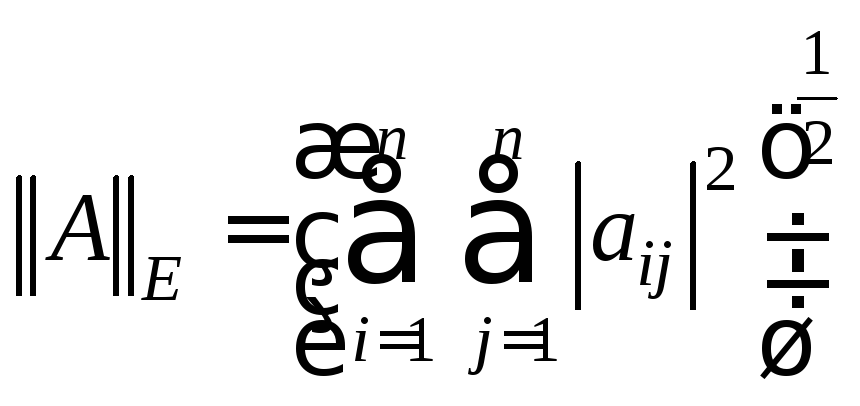- евклидова норма или норма Фробениуса

-

- спектральная норма

где - собственные значения симметричной матрицы(сингулярные числа матрицыА). Обе указанные нормы согласованы с эвклидовой нормой вектора .

-

- столбцовая норма (norm(a,1)). (Согласована с векторной нормой ).

-

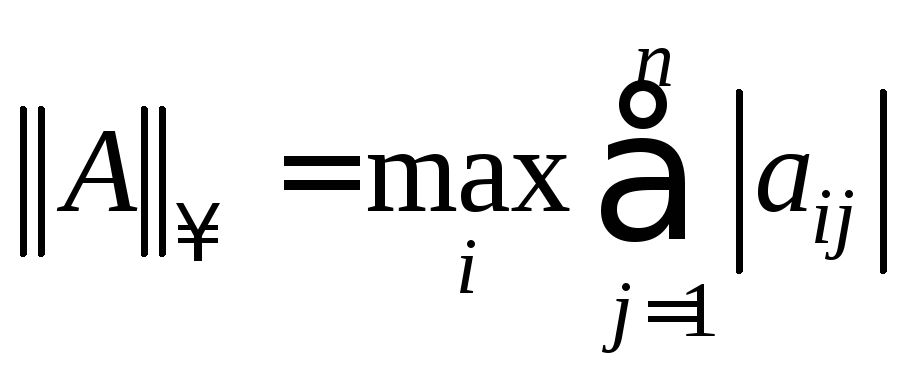- строчная норма (norm(a,inf)). (Согласована с ).

Замечание. Из всех приведенных матричных норм, согласованных с евклидовой нормой вектора, спектральная норма принимает минимальное значение.

Определение 3. Число (вообще говоря, комплексное) называется собственным значением матрицы А, соответствующим собственному вектору x, если выполняется условие:

.

(20)

Определение 4. Множество всех собственных чисел матрицы А , записанных с учетом их кратности, называетсяспектром матрицы А и обозначается S(A).

Определение 5. Спектральным радиусом r(A) квадратной матрицы А называется максимальное по модулю собственное значение матрицы A.

Определение 6. Сингулярным числом матрицыА называется собственное значение матрицы .

Определение 7. Матрица А называется положительно (неотрицательно) определенной (пишут: или ), если соответствующая квадратичная форма

.

Простейшие следствия из определений.

Следствие 1. (Критерий Сильвестра). все ведущие угловые миноры матрицыА положительны. доказывается в курсе линейной алгебры

Следствие 2. , причем.

следует из критерия Сильвестра.

Следствие 3. все собственные значения. (Для).

Пусть - собственное значение, соответствующее собственному векторуv. По условию

.

Следствие 4. Пусть А – вещественная матрица матрица.

Имеем: {по свойству скалярного произведения}.

Следствие 5. Сингулярные числа вещественной матрицы А – неотрицательны.

Следует из С.3 и С.4.

Следствие 6. Пусть А – вещественная и симметрическая матрица .

Имеем: .

Следствие 7. Если А – невырожденная матрица собственные значения матрицА и A^-1 взаимообратны.

Пусть результат.