Метод Гаусса с выбором главного элемента
Основное накопление погрешностей решения в методе Гаусса происходит на этапе приведения системы к треугольному виду. Механизм накопления основной части этой погрешности заключается в привнесении погрешностей вычисления коэффициентов ведущего уравнения в коэффициенты последующих уравнений при исключении каждого очередного неизвестного. Анализ соотношений метода Гаусса показывает, что погрешности вычисления коэффициентов ведущего уравнения привносятся в соответствующие коэффициенты всех последующих уравнений в долях отношений этих коэффициентов к диагональному (главному) коэффициенту ведущего. В связи с этим привносимая погрешность будет тем меньше, чем меньше доли этих отношений. Поэтому в методе Гаусса с выбором главного элемента на каждом шаге исключения i-го неизвестного в качестве ведущего используется уравнение (с i-го по n-ое), содержащее максимальный по модулю коэффициент – главный элемент. При этом в качестве него может использоваться один из коэффициентов i-го столбца, i-ой строки или всей непреобразованной части матрицы. Первый подход называется выбором главного элемента по столбцу, второй – по строке, а третий – по всей матрице. При использовании двух последних происходит перестановка столбцов матрицы системы. Это приводит к изменению порядка следования компонент вектора неизвестных и требует его восстановления по окончании процесса решения.
В качестве примера применения метода Гаусса можно рассмотреть задачу отыскания решения следующей системы уравнений
при ограничении разрядной сетки вычислений до трёх знаков и с оценкой погрешности получаемого решения.
Поставленная задача будет решаться методом Гаусса с выбором главного элемента по столбцу.
1. Прямой ход.
а. Выбор главного элемента среди элементов первого столбца
б. Нормировка первого уравнения
в. Исключение элементов первого столбца
г. Выбор главного элемента среди элементов второго столбца второго и третьего уравнений
д. Нормировка второго уравнения
е. Исключение элементов второго столбца
ё. Нормировка последнего уравнения
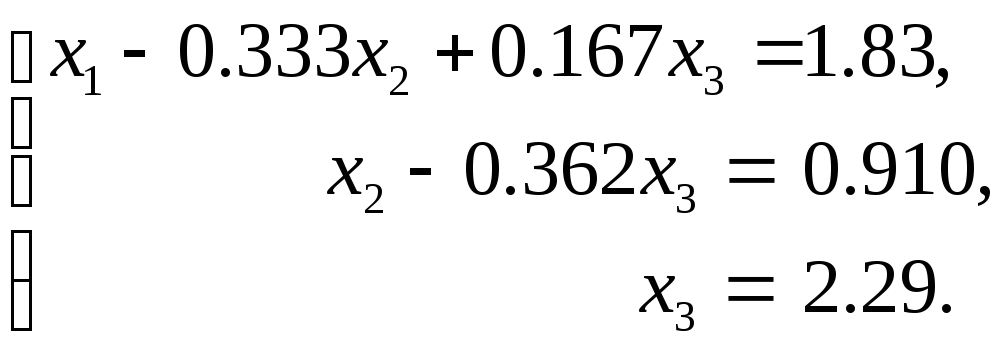
2. Обратный ход
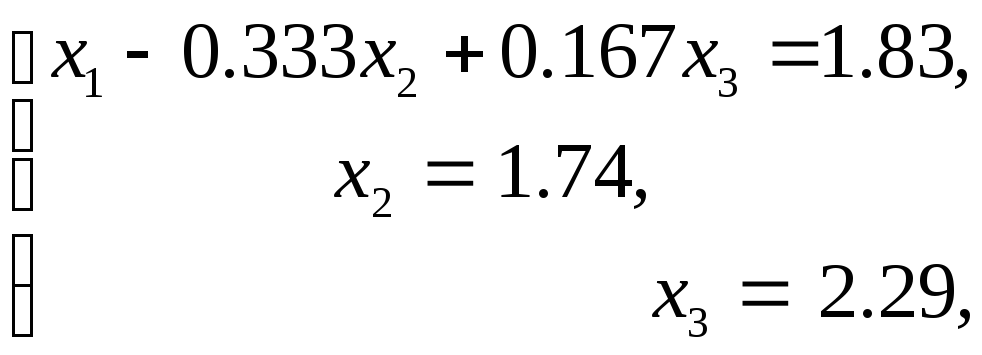
В итоге получено решение системы уравнений
.
3. Погрешность найденного решения.
а. Пересчёт вектора правых частей системы
.
б. Формирование системы уравнений, определяющей погрешности решения
,
то есть
.
в. Решение системы относительно погрешностей выполняется аналогично пунктам 1 и 2. Прямой ход (пункт 1) даёт следующую систему с верхней треугольной матрицей
а обратный ход позволяет получить решение
.
г. Оценка абсолютной и относительной погрешностей решения системы линейных алгебраических уравнений
,
,
.
LU-разложение
В среде Matlab’а используется модификация метода Гаусса, основанная наLU-разложении матрицы системы. Этот метод отличается от метода Гаусса только вычислительным алгоритмом для правых частей системы на этапе прямого хода. Его суть состоит в следующем.
Когда система линейных алгебраических уравнений
или
решается методом Гаусса, то прямой ход решения состоит из (n–1)-го шагов.
На
первом шаге исключается неизвестное
x1из уравнений,
начиная со 2-го. Пусть
,
тогда он называется ведущим элементом
этого первого шага. В противном случае
выполняется операция выбора главного
элемента. Далее находятся величины
,
и как в методе Гаусса производится
вычитание первого уравнения, умноженного
наμi1,
последовательно из всех уравнений,
начиная со 2-го. Эта операция обращает
в нуль коэффициенты приx1в этих уравнениях. В результате получается
система следующего вида:
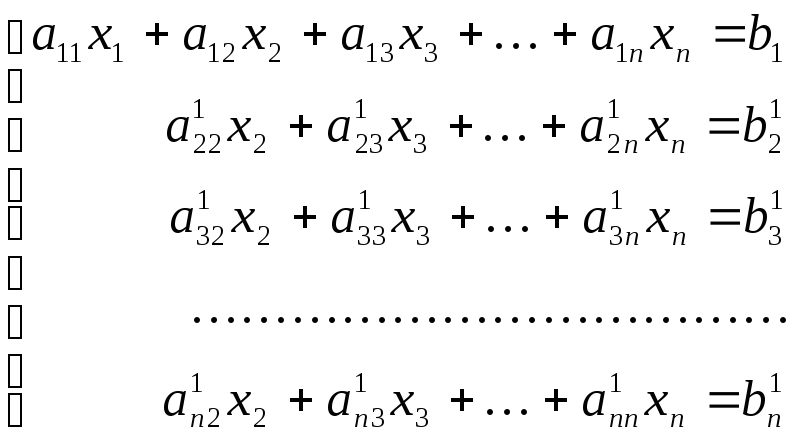или
,
в которой
и
.
Этот шаг прямого хода для матрицы системы и вектора её правых частей посредством введения матрицы
записывается
в виде
.
На
втором шаге прямого хода исключается
x2из всех
уравнений, начиная с 3-го. Для этого в
предположении о том, что
,
вычисляются множители
,
и последовательно вычитают второе
уравнение системы умноженного наμi1,
из остальных её уравнений, начиная с
3-го. Этот шаг записывается через матрицу
аналогично предыдущему шагу
или, с учётом первого шага, следующим образом
.
Далее шаги прямого хода повторяются, и на последнем (n–1)-м шаге вводится матрица
,
с помощью которой верхняя треугольная матрица, являющаяся результатом прямого хода метода Гаусса, записывается в виде
или, с учётом предыдущих шагов, следующим образом
.
Из первого выражения получается следующее представление матрицы исходной системы линейных алгебраических уравнений
,
где обычным перемножением матриц можно легко убедиться, что
,
,
…,
.
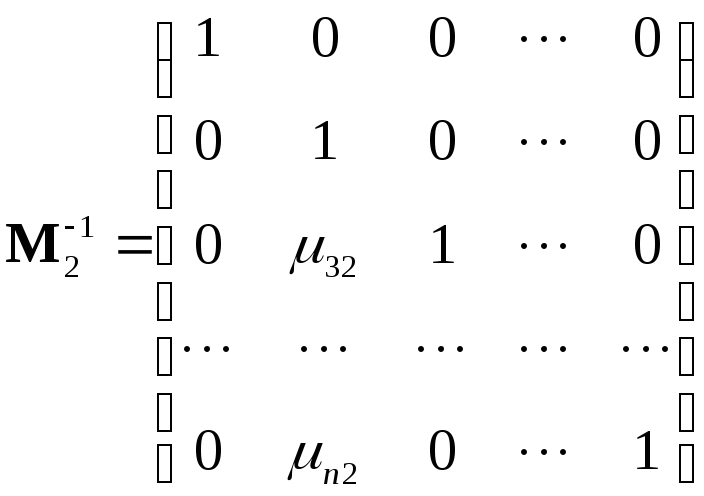Если ввести обозначение
,
в котором матрица Lявляется нижней треугольной
,
в чём можно
убедиться перемножением матриц
,
а матрицаU– верхней
треугольной, поскольку является
результатом прямого хода метода Гаусса,
то матрица исходной системы линейных
алгебраических уравнений приобретает
вид
.
Результатом такой организации алгоритма метода Гаусса является следующий трёхэтапный ход решения исходной системы линейных алгебраических уравнений в Matlab’е:
производятся вычисления матриц L и U, в соответствии с алгоритмом метода Гаусса;
решается вспомогательная система линейных алгебраических уравнений с нижней треугольной матрицей
.
Алгоритм этого этапа повторяет обратный ход метода Гаусса.
решение исходной системы линейных алгебраических уравнений ищется как решение системы уравнений с вехней треугольной матрицей
.
Ход этого решения тоже повторяет обратный ход метода Гаусса.
Замечание. При необходимости применения операции выбора главного элемента, для учёта перестановка строк и столбцов матрицы на каждом шаге получения матрицLиUпроизводится умножение матрицы системы на матрицуPk, описывающую перестановкуk-ой строки с некоторой строкой с номеромi(i>k). При этом
,
а LUразложение получаеся не для матрицыA, а для матрицы
.
отличающейся от Аперестановкой строк
.
Итерационные методы. К этим методам относятся метод простых итераций, метод Зейделя и ряд других. Методы этой группы обладают высокой эффективностью, но их применение связано с рядом ограничений, накладываемых на свойства матрицы A.