Относительная разница между значениями приближения корня на третьей и четвёртой итерациях составляет

.

Таким образом, если в задаче требовалось бы вычислить значение корня с относительной разностью δ_отн=0.00002, то уточнение значения корня можно прекратить. Однако истинное значение оценки относительной погрешности вычисления будет определяться по формуле

.

Для определения значения M, предполагая монотонность первой производной функции φ(x) на отрезке [x₀, x₄], достаточно вычислить её значения при x₀ = 1.5 и x₄ = 1.53202 и взять из них наибольшее по модулю

= 1 –0.6(3·1.5²– 14.6·1.5 + 16.8) = 0.01,

= 1 –0.6(3·1.53202²– 14.6·1.53202 + 16.8) = 0.11574,

М= 0.11574,

откуда

.

Аналогичную оценку относительной погрешности можно получить, рассмотрев только последнюю итерацию

= 1–0.6(3·1.5320²– 14.6·1.5320 + 16.8) = 0.11567,

= 1–0.6(3·1.53202²– 14.6·1.53202 + 16.8) = 0.11574,

М= 0.11574,

откуда

.

Полученные значения оценки относительной погрешности отличаются друг от друга в два раза. Однако это не должно вызывать недоумения, поскольку полученные числа – не значения погрешности, а всего лишь её оценки сверху.

Метод Ньютона (I.Newton, 1669, Mr.Raphson, 1720)

В данном методе каждое новое приближение к значению корня уравнения f(x) = 0 ищется по следующей итерационной схеме

………………….

………………….

где x₀ – первоначальное приближенное значение корня, взятое с отрезка [a, b] локализации точного решения уравнения.

Если последовательность значений x_k (k = 0, 1, 2,...) сходится к точному значению корня x_т, то абсолютная погрешность значения корня на k-ом шаге (x_k) определяется выражением

,

где

, , ,.

Вычисление относительной погрешности и формулировка условия окончания процесса уточнения значения корня осуществляется так же, как это было описано выше в методе итераций. Аналогично формулируется и условие сходимости метода Ньютона

.

При решении практических задач точное значение x_т корня уравнения неизвестно. Поэтому вместо приведённого неравенства, описывающего условие сходимости, используется следующее

,

где

, ,

а вместо описанной выше оценки для абсолютной погрешности в случае сходимости итераций метода Ньтона–Рафсона после 2-й итерации используют более грубую оценку

.

Г

Рис.5.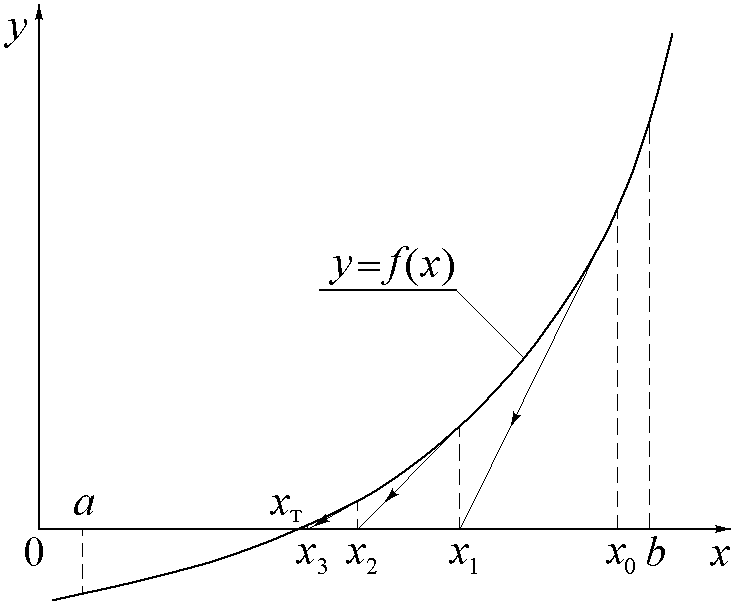

рафическая интерпретация работы метода Ньютона показана на рис.5. Из точки на кривойy = f(x), имеющей абсциссу x₀, проводится касательная до пересечения с осью 0x. Абсцисса точки пересечения принимается за новое приближение значения x₁ корня уравнения f(x) = 0. В случае сходимости последовательности вычисляемых значений x₀, x₁,…, x_k,… процесс продолжается до тех пор, пока не выполнится условие окончания процесса уточнения значения корня.

Методы сужения отрезка [a, b], к которым относятся метод хорд, метод половинного деления и другие, не имеют ограничений на функцию f(x), присущих методам последовательного уточнения.

Метод половинного деления (метод бисекций)

Работа метода иллюстрирована рис.6. Отрезок локализации [a, b] корня делится пополам

x₁= (a + b)/2

и

Рис.6.

в полученной точке вычисляется значение функции. Еслиf(x₁) = 0, то корень найден и расчёты прекращают. В противном случае выбирается новый отрезок, содержащий корень уравнения, из отрезков [a, x₁] и [x₁, b]. На концах искомого отрезка функция f(x) должна иметь значения разного знака. Для это­го проверяется условие f(a)·f(x₁) < 0. При его выполнении в качестве нового отрезка принимается отрезок [a, x₁], в противном случае – [x₁, b]. Процесс вычисления значения корня продолжается до тех пор, пока не будет выполнено требование к точности его определения. В данном случае оценка абсолютной погрешности определения корня

совпадает с длиной отрезка его последней локализации. В свою очередь относительная погрешность вычисляется как

.

При этом за значение корня принимается либо одна из границ суженного отрезка [a, b], либо его середина.

Алгоритм метода может быть проиллюстрирован на примере рассмотренного выше уравнения

x³ – 7.3x² + 16.8x – 12.2 = 0.

В качестве отрезка локализации выбирается отрезок [1.5, 1.6], содержащий первый корень уравнения (см. рис.4). На первом шаге уточнения корня вычисляются значения функции на границах выбранного отрезка

f(1.5) = 1.5³ – 7.3·1.5² + 16.8·1.5 – 12.2 = –0.05,

f(1.6) = 1.6³ – 7.3·1.6² + 16.8·1.6 – 12.2 = 0.088.

Затем в середине интервала x₁ = 1.55 также вычисляется значение функции

f(1.55) = 1.55³ – 7.3·1.55² + 16.8·1.55 – 12.2 = 0.0256.

Так как эта точка не соответствует корню уравнения, то определяется новый отрезок его локализации. Для этого проверяется знак произведения значений функции на левой границы отрезка локализации корня и в его центре f(1.5)·f(x₁). Из расчётов видно, что это произведение меньше нуля, значит, в качестве нового отрезка локализации корня должен приниматься отрезок [1.5, 1.55].

Для выполнения второго шага уточнения корня значения функции на границах нового отрезка локализации считать не нужно, они уже известны: f(1.5) = –0.05; f(1.55) = 0.0256. Достаточно вычислить её значение в середине нового отрезка локализации x₂ = 1.525

f(1.525) = 1.525³ – 7.3·1.525² + 16.8·1.525 – 12.2 = –0.0105.

Так как произведение f(1.5)·f(x₂) больше нуля, то в качестве нового отрезка локализации принимается отрезок [1.525, 1.55]. Аналогично выполняются шаги c третьего по седьмой, дающие следующие значения приближения корня

x₃= 1.5375 – центр отрезка [1.525, 1.55],

x₄= 1.53125 – центр отрезка [1.525, 1.5375],

x₅= 1.53438 – центр отрезка [1.53125, 1.5375],

x₆= 1.53281 – центр отрезка [1.53125, 1.53438],

x₇= 1.53203 – центр отрезка [1.53125, 1.53281].

Значение относительной погрешности вычисления приближения x₇= 1.53203 корня уравнения будет определяться по формуле

.

Эта величина совпадает с длиной отрезка локализации найденного приближения корня, отнесённой к величине этого приближения

.

Таким образом, если в задаче требовалось бы вычислить значение корня с относительной погрешностью ε_отн= 0.001, то уточнение значения корня можно прекратить.