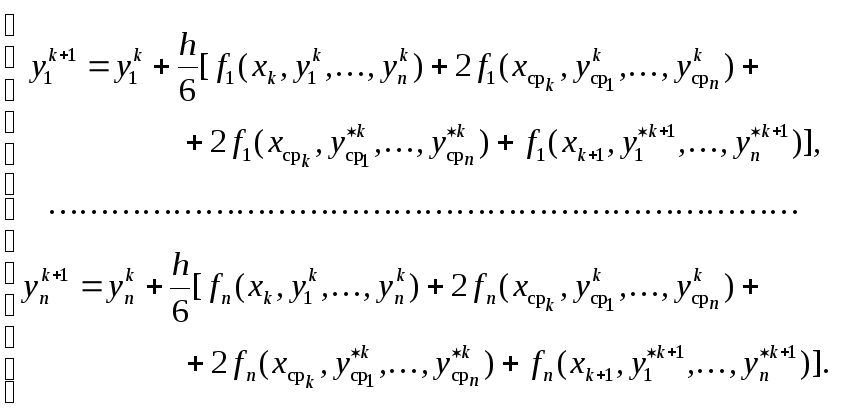Контрольные задания

Получить решение задачи Коши на указанном отрезке с использованием ме­тода из числа рассматриваемых в этом разделе. Подобрать величину шага интегрирования так, чтобы относительная погрешность решения задачи не превышала 0.1%.

1. .

2. .

3. .

4. .

5. .

6. .

7. .

8. .

9. .

10. .

11. .

12. .

13. .

14. .

15. .

16. .

17. .

18. .

19. .

20. .

21. .

22. .

23. .

24. .

25. .

26. .

27. .

28. .

29. .

30. .

7. Решение задачи коши для нормальных систем обыкновенных дифференциальных уравнений и уравнений высших порядков Справочная информация

Задача Коши для нормальной системы обыкновенных дифференциальных уравнений записывается в виде

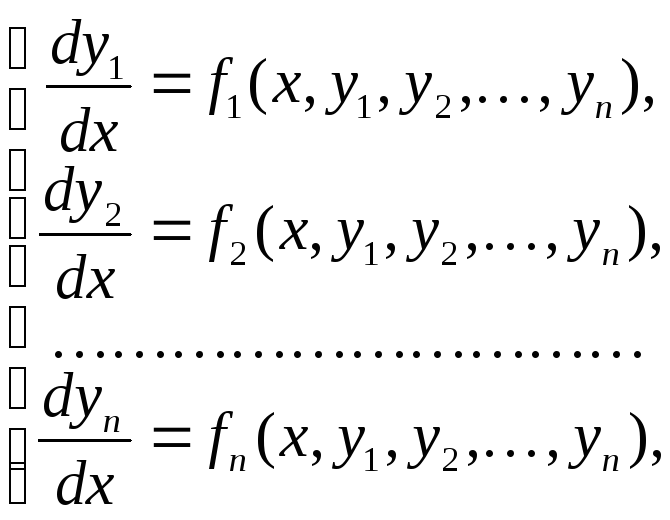
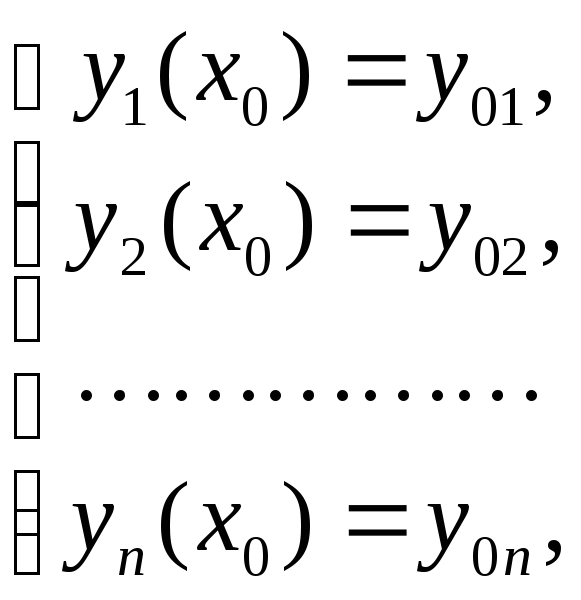
или в матричной форме

, ,

где

, ,.

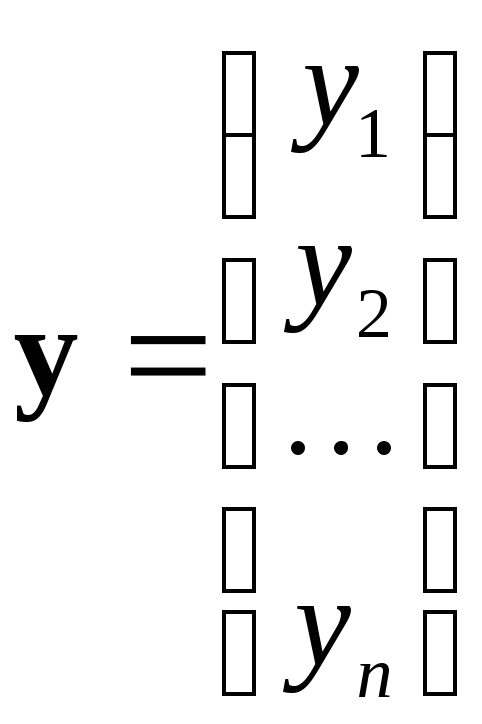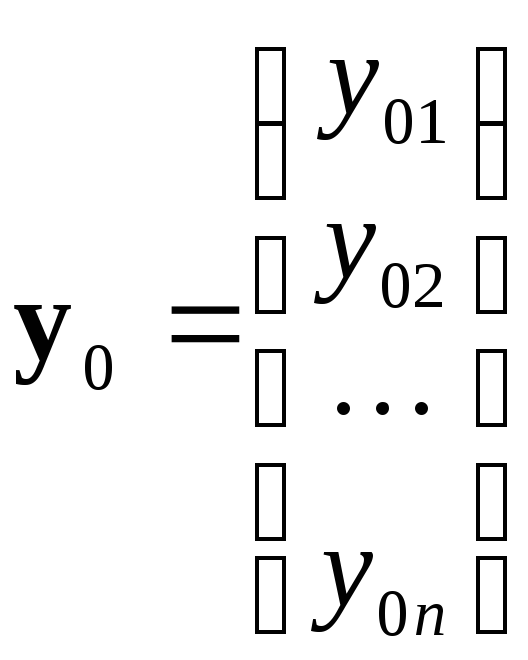Система дифференциальных уравнений связывает независимую переменную x, искомые функции y₁, y₂,..., y_n и их первые производные. В данном случае решение задачи Коши заключается в отыскании функций y₁ = y₁(x), y₂ = y₂(x),..., y_n = y_n(x), обращающих каждое уравнение системы в тождество на конечном или бесконечном интервале (a, b) и удовлетворяющих начальным условиям.

Такая форма записи задачи Коши является канонической для систем обыкновенных дифференциальных уравнений. К ней могут быть приведены как любые другие формы представления систем дифференциальных уравнений, разрешённых относительно старших производных, так и дифференциальные уравнения высших порядков. Приведение дифференциальных уравнений высших порядков к нормальной системе дифференциальных уравнений осуществляется по следующей схеме. Если дана задача Коши вида

,

, ,, … ,,

то замена переменных

, ,, … ,,

сводит её к нормальной системе дифференциальных уравнений с начальными условиями

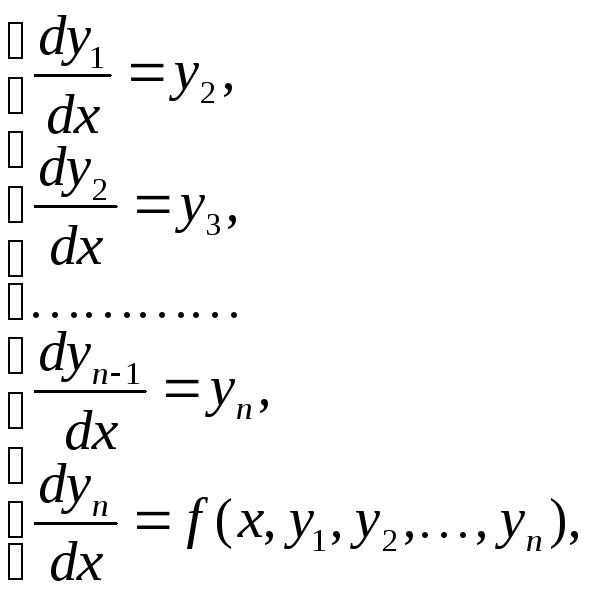
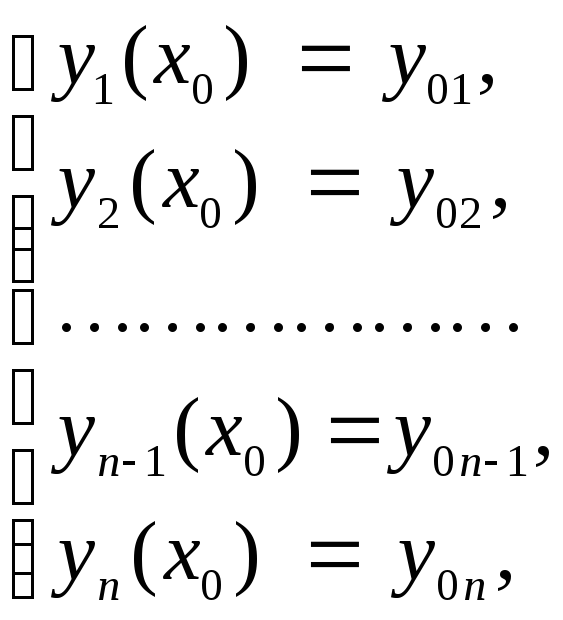
образующих задачу Коши.

Для решения такой задачи Коши используются те же методы, что для обыкновенных дифференциальных уравнений 1-го порядка. Это обуславливается тем, что матричная форма записи задачи Коши для нормальной системы полностью совпадает с её формулировкой для этих уравнений. Аналогична для неё и теорема о существовании единственного решения. Единственным отличием здесь является то, что вместо функций y(x) и f(x, y) используются вектор-функции y и f, состоящие из n функций y₁(x), y₂(x),..., y_n(x) и f₁(x, y₁,..., y_n), f₂(x, y₁,..., y_n),..., f_n(x, y₁,..., y_n), соответственно. При этом расчётные схемы методов и оценки их погрешностей сохраняются.

Метод Эйлера

Соотношения метода Эйлера для нормальной системы в матричной форме имеют вид

,

или в развёрнутой форме

,

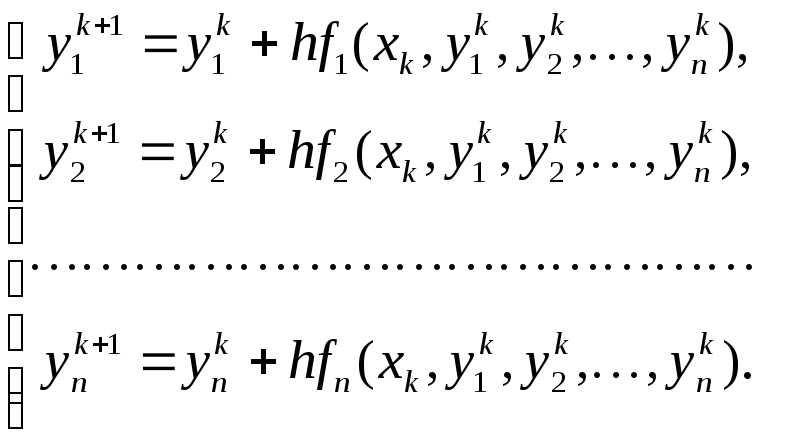
где верхний индекс показывает номер шага по аргументу x.

Геометрическая интерпретация работы метода Эйлера при решении задачи Коши для нормальной системы идентична его геометрической интерпретации для дифференциальных уравнений 1-го порядка. Однако в данном случае движение осуществляется вдоль некоторой кривой в (n + 1)-мерном пространстве переменных x, y₁, y₂,..., y_n, которая является геометрическим представлением вектор-функции y.

Усовершенствованный метод Эйлера

Основные соотношения усовершенствованного метода Эйлера в матричной форме записываются следующим образом

, ,

, ,

что в развёрнутом виде даёт

,

,

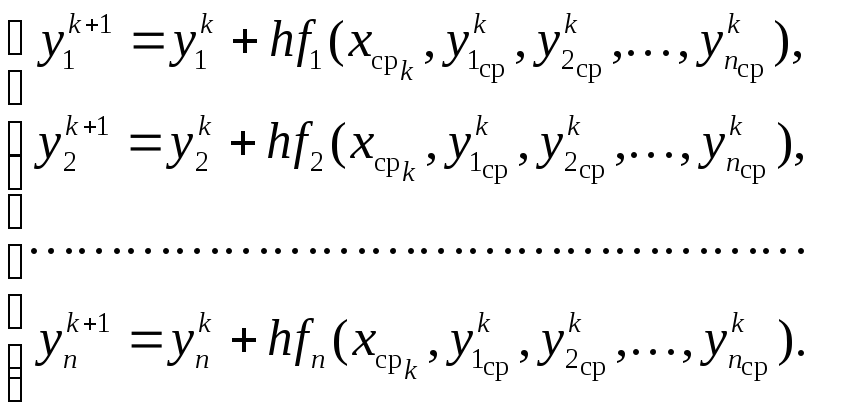
Метод Рунге–Кутта

Преобразование соотношений метода Рунге–Кутта 4-го порядка точности на случай решения нормальной системы дифференциальных уравнений в мат­ричной форме приводит к следующему

, ,

,

, ,

.

Как видно из приведённых формул, алгоритм метода строится по той же схеме из 4-х шагов, но в (n+1)-мерном пространстве. При этом направ­ление отыскания следующей точки приближённого решения определяется вектором, каждая ком­понента которого вычисляется как некоторое осреднённое значение танген­са угла между касательной к интегральной гиперкривой и осью аргумента системы x.

В развёрнутом виде соотношения метода Рунге–Кутта для нормальной системы из n уравнений записываются в виде

,

,
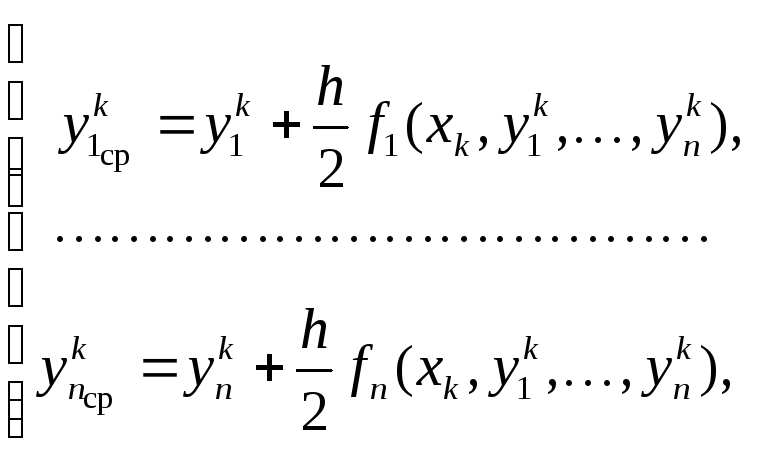
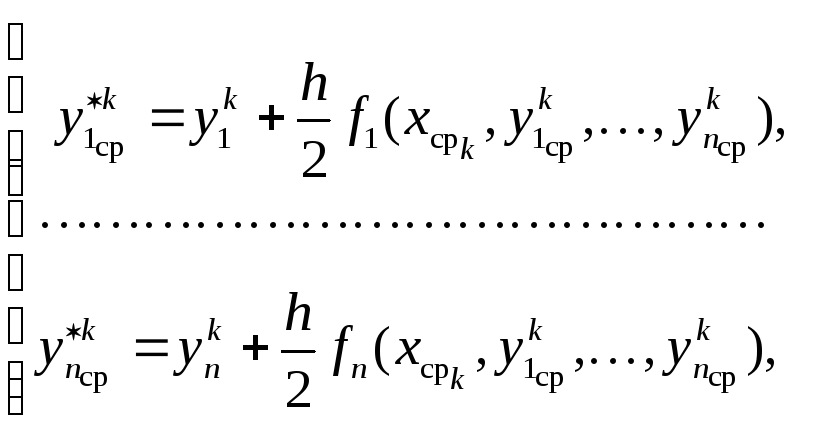