Оценка погрешностей методов

Все оценки погрешности, полученные для решений задачи Коши для одного дифференциального уравнения 1-го порядка, остаются справедливыми и для решения систем аналогичных дифференциальных уравнений. В силу этого абсолютная погрешность метода Эйлера на каждом шаге пропорциональна величине h²

.

Здесь

,

где

.

При вычислении коэффициента C_k+1 в качестве вектор-функции используется некая промежуточная функция, кривая которой в (n+1)-мерном пространстве переменных x, y₁, y₂,..., y_n, располагается между кривыми приближённого и неизвестного точного решений.

Абсолютная погрешность усовершенствованного метода Эйлера на каждом шаге пропорциональна величине h³

.

где

,

,

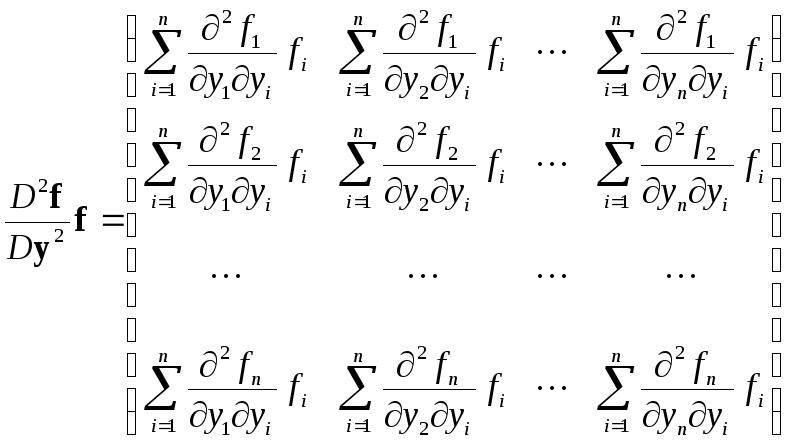а метода Рунге–Кутта 4-го порядка – h⁵

,

где выражение для коэффициента C_k+1, аналогичное записанным для методов Эйлера, не приводится из-за своей громоздкости.

Абсолютная погрешность вычисления приближённого решения на отрезке интегрирования системы дифференциальных уравнений после n-го шага оценивается следующим образом

,

где m = 2 для метода Эйлера, m = 3 для усовершенствованного метода Эйлера и m = 5 для метода Рунге–Кутта 4-го порядка и

, .

На практике такое вычисление абсолютных погрешностей решения задачи Коши затруднено. Поэтому, как правило, для вычисления погрешности методов используют апостериорную оценку, базирующуюся на правиле Рунге

,

где y(x_n, h) и y(x_n, 2h) – приближённые значения вектора решения, вычисленные в точке x_n при шагах интегрирования, отличающихся друг от друга в два раза.

В качестве относительной погрешности решения задачи Коши на отрезке [x₀, x_n], как и в случае одного дифференциального уравнения 1-го порядка, используют интервальную оценку

.

Алгоритмы методов решения задачи Коши и оценка погрешности получаемых результатов могут быть проиллюстрированы на примере решения уравнения с начальными условиямиy(0) = 0,на отрезке [0, 0.4] с шагомh= 0.1.

На первом этапе дифференциальное уравнение 2-го порядка должно быть преобразовано к эквивалентной системе дифференциальных уравнений 1-го порядка. Для этого вводятся следующие обозначения

,

что позволяет записать исходную задачу Коши в виде системы

В соответствии с алгоритмом метода Эйлера рас­чётная схема решения системы дифференциальных уравнений может быть представлена в виде следующих соотношений

,

Таким образом, процесс решения с заданным шагом интегрирования h = 0.1 будет выглядеть следующим образом

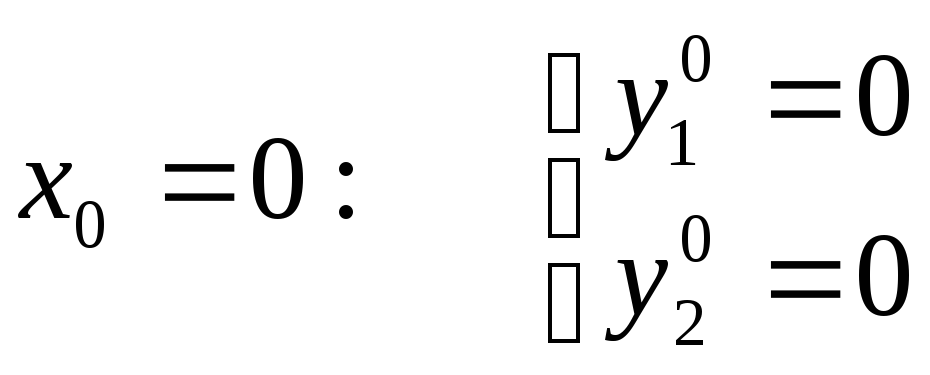
Для получения оценки погрешности решения необходимо повторить про­деланные расчёты с удвоенным шагом h = 0.2

Эти результаты позволяют оценить абсолютную и относительную погрешности решения с шагом интегрирования h = 0.1

,

,

,

,

,

, ,

,

,

, .

Из этих расчётов видно, что решение рассматриваемой задачи Коши методом Эйлера с шагом 0.1 на отрезке [0, 0.4] получено с относительной погрешностью не большей, чем 5.1%.

Пример решения на пэвм в среде Matlab

Условия задачи.Получить решение задачи Коши

на отрезке [0, 10] с использованием метода Эйлера.

Решение. Для численного решения исходной задачи Коши её необходимо преобразовать к эквивалентной нормальной системе дифференциальных уравнений. Это достигается путём введения следующего обозначения искомого решения задачи Коши и его производной

.

Такая замена позволяет свести исходную задачу Коши к системе из двух обыкновенных дифференциальных уравнений 1-го порядка и соответствующим им двум новым начальным условиям

Для численного решения рассматриваемой задачи Коши с помощью встроенной функции ode45, реализующей методы Рунге–Кутта 4-го и 5-го порядков, сначала надо сформироватьm-файл, который будет вычислять правые части системы дифференциальных уравнений. Например, с именемvdpol.m:

function ydot = vdpol(x,y)

ydot = [y(2); y(2).*(1-y(1).^2)-y(1)];

Теперь программу решения задачи Коши с отображением решения в графическом окне можно представить в следующем виде

x0 = 0;

y0 = [0 0.25]; ←начальные условия

xf = 10; ←правая граница построения отрезка решения

[x,y] = ode45('vdpol', x0, xf, y0)

plot(x,y), grid

Запуск этой программы на выполнение позволяет получить таблицу значений аргумента xи вектора решенияy:

x =

0

0.0003

0.0019

0.0099

0.0499

0.2499

......

10.0000

y =

0 0.2500

0.0001 0.2501

0.0005 0.2505

0.0025 0.2525

0.0128 0.2625

0.0703 0.3117

................

-0.1009 -2.2684

и графики (см. рис.1), на которых выведены значения полученного приближенного решения и его производной.

Погрешность полученного решения явно не задавалась. Однако, по умолчанию абсолютная погрешность решения, получаемого при использовании функции ode45, равна 10^–6. Поэтому, имея в виду полученные значенияyи, можно утверждать, что относительная погрешность данного решения не превосходит 10^–5.

Рис.1.

При необходимости прямой реализация решения рассматриваемой задачи Коши методом Эйлера с оценкой его относительной погрешности по правилу Рунге может быть использована программа следующего содержания:

a=0; ←левая граница отрезка посроения решения

b=10; ←правая граница отрезка посроения решения

n=10000; ←число шагов по отрезку посроения решения

Y(1,1)=0; Y(2,1)=0.25; ←начальные условия

x(1)=a; h=(b-a)/n

for i=2:n+1

x(i)=a+(i-1)*h;

y(1,i)=y(1,i-1)+h*y(2,i-1);

y(2,i)=y(2,i-1)

+h*(y(2,i-1).*(1-y(1,i-1).^2)-y(1,i-1));

end

n1=n/2; ←повтор решения с удвоенным числом шагов

y1(1,1)=0; y1(2,1)=0.25;

x1(1)=a; h1=(b-a)/n1

for i=2:n1+1

x1(i)=a+(i-1)*h1;

y1(1,i)=y1(1,i-1)+h1*y1(2,i-1);

y1(2,i)=y1(2,i-1)

+h1*(y1(2,i-1).*(1-y1(1,i-1).^2)-y1(1,i-1));

end

maxy(1)=1; ←начало вычисления относительной погршности

for i=2:n1+1

maxy(i)=(max(Y(1,1:2:2*i)));

end

dy=(abs(Y1(1,1:n1+1)-Y(1,1:2:n+1)))./(maxy);

y2=[x1.',y(1,1:2:n+1).',y1(1,:).',dy.']←массив вывода графиков

plotyy(x,y(1,:),x1,dy),grid

Функция plotyy выводит два графика с разным масштабирование функций. Ось первого графика – решения у отображена слева (см. рис.2), а второго графика – относительной погрешности ε_отн, обозначенной в программе dy – справа. На рис.2 видно, что относительная погрешность полученного решения не превосходит 1.2%.

Рис.2.