Контрольные задания

Выбрать один из методов интерполяции, позволяющий сформировать образ кривой, визуально совпадающий с графиком заданной функции. В качестве такой функции взять левую часть алгебраического уравнения из раздела «Решение нелинейных уравнений», которое соответствует номеру выполняемого варианта. В качестве отрезка интерполяции использовать указанный там же отрезок поиска корней. Точки интерполяции (в количестве 11 штук) равномерно распределить на заданном отрезке.

5. Аппроксимация таблично заданных функций Справочная информация

И

Рис.1.

нтерполяция на практике используется только в тех случаях, когда значения координат узлов таблично заданной функции не искажены случайными ошибками. Наличие ошибок в значенияхyтаблично заданной функции приводит к неправильному представлению о поведении реальной функции и делает бес­смыс­ленной её интерполяцию. В этом случае необходимо строить «сглаживающую» при­­ближающую функцию, отражающую физику моделируемого процесса. Её график не обязан проходить через все узловые точки табличной функции, как показано на рис.1. Построение таких приближающих функций носит название аппро­ксимации.

Через множество узловых точек таблично заданной функции можно провести бесконечное количество аппроксимирующих кривых. Задача выбора единственной из них делится на две основные подзадачи:

• выбор аналитических зависимостей, отражающих физику взаимосвязи аргумента и реальной функции, когда должен быть определён общий вид приближающей функции;

• выбор критерия достоверности описания реальной функции с помощью выбранных зависимостей.

Существует множество подходов к построению вида приближающей функции, как функции с параметрами. Одним из них является выбор в качестве аппроксимирующей зависимости линейной комбинации некоторых известных аналитических функций. Вместе они должны отражать суть процесса, описываемого исходной функцией, и быть линейно независимыми на отрезке аппроксимации [x₁,x_n]

.

Функции φ_k(x) часто выбираются в виде полиномов, частным случаем которых являются степенные функции

φ₁(x) = 1, φ₂(x) = x, φ₃(x) = x², φ₄(x) = x³,…,

в виде тригонометрических косинусов

,

или в любом другом удобном для исследователя виде.

Другим подходом к построению приближающей функции является её представление сплайнами. Это избавляет исследователя от необходимости подбирать аналитические функции для аппроксимирующей зависимости и часто даёт результат, отвечающий всем требованиям, которые предъявляются к процессу аппроксимации.

В качестве критерия достоверности описания реальной функции Гауссом (1794) и Лежандром (A.M.Legendre, 1805) было предложено использовать сумму квадратов отклонений значений аппроксимирующей функции от ординат узлов таблично заданной

,

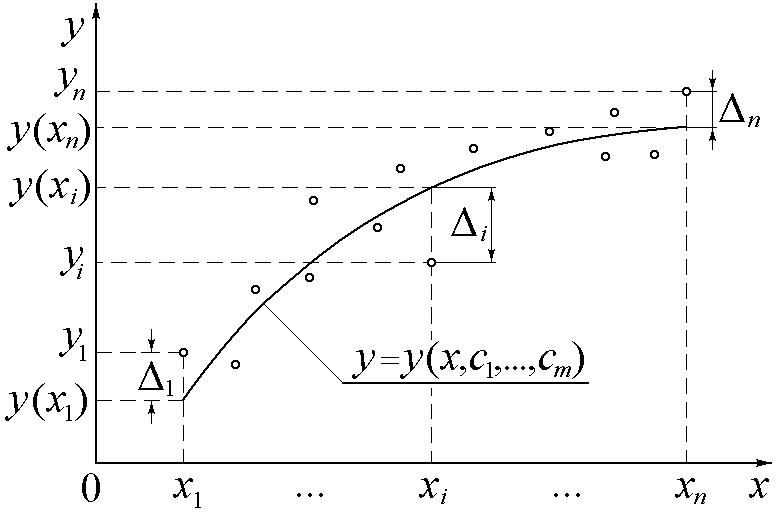где отклонение от каждой узловой точки Δ_i, показанное на рис.2, вычисляется как

.

С

Рис.2.

умма квадратов отклонений F при таком представлении является квадратичной функцией от параметров аппроксимации c₁, c₂,..., c_m. Очевидно, что чем меньше значение функции F, тем лучше выбранная аппроксимирующая функция описывает реальную функцию. Следовательно, задача аппроксимации сводится к определению значений параметров c₁, c₂, ..., c_m, которые минимизируют значение критерия – функции F. Этот приём получил название «метод наименьших квадратов».

Необходимым условием экстремума функции многих переменных F является равенство нулю всех её частных производных по параметрам c₁, c₂, ..., c_m

.

Можно показать, что для функции F, являющейся суммой квадратов отклонений, достаточные условия существования её минимума в стационарной точке выполняются тождественно. Поэтому необходимыми условиями существования экстремума функции F можно пользоваться как условиями её минимума, что позволяет привести задачу аппроксимации n значений табличной функции к задаче решения системы из m линейных алгебраических уравнений относительно этих параметров с симметричной матрицей

где

,

.

Параметры аппроксимации c₁,c₂,...,c_m, определяемые как решение вышеприведённой системы линейных уравнений, которая сформирована для заранее выбранных функцийφ₁(x),φ₂(x), …,φ_m(x), дают наименьшее значение целевой функцииF. Для каждого набора таких функций будет получаться своё наименьшее значениеF. Поэтому для выбора наилучшей аппроксимации ориентируются на наименьшее значение погрешности аппроксимации, которая рассчитывается следующим способом для каждого набора функцийφ₁(x),φ₂(x), …,φ_m(x)

, ,

где под нормой таблично заданной функции понимается евклидова, квадратичная норма

.

Р

Рис.3.

абота метода может быть проиллюстрирована на примере аппроксимации функции, заданной 8-ю узловыми точками на рис.3, и поиска её значения прих = 1.5.

Для построения зависимости, аппроксимирующей таблично или графически заданную функцию, исследователь должен подобрать аналитические функции, которые своей комбинацией отражают описываемый процесс. В данном случае исходная функция может быть описана комбинацией двух функций. Первая из них должна отражать обратно пропорциональную зависимость функции от аргумента в диапазоне от 0 до 2, а вторая – прямо пропорциональную зависимость в диапазоне от 2 до 4. Таким образом, в качестве аппроксимационной зависимости может быть принята следующая

.

Необходимо заметить, что данное представление аппроксимирующей зависимости не является единственным. Можно подобрать и другие комбинации элементарных функций, которые отражают общий характер рассматриваемой табличной функции.

В соответствии с приведённым выше алгоритмом сумма Fквадратов отклонений ординат аппроксимирующей функции от ординат узловых точек записывается в виде

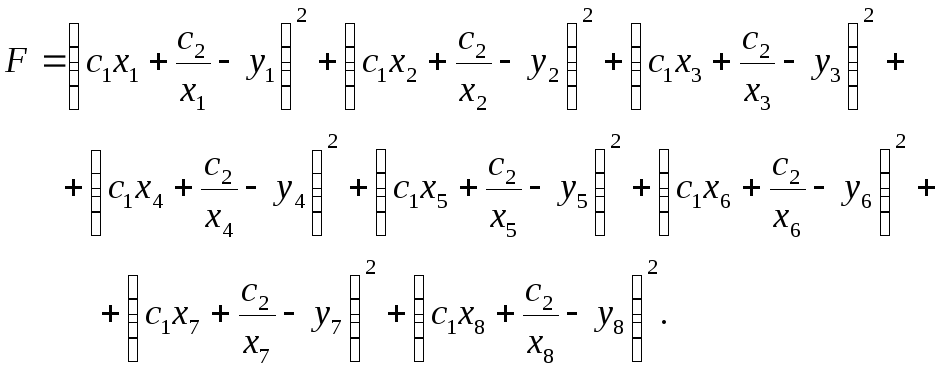
Вычисления по этой формуле удобнее выполнять, сняв с графика координаты узловых точек и сформировав из них следующую таблицу.

i	1	2	3	4	5	6	7	8
x	0.5	0.5	1	1.5	1.5	2.5	3.5	4
y	0.9	0.8	0.5	0.5	0.4	0.4	0.5	0.5

В этом случае сумма квадратов отклонений будет

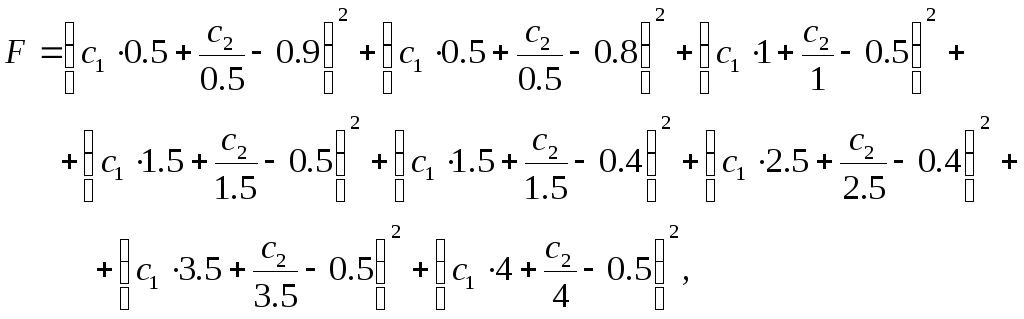
а её частные производные по параметрам c₁иc₂, соответственно

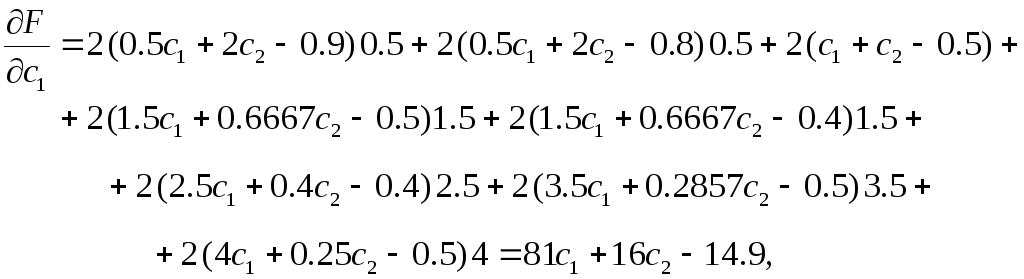
Исходя из условия равенства нулю полученных частных производных, решение задачи сводится к решению системы из двух линейных алгебраических уравнений

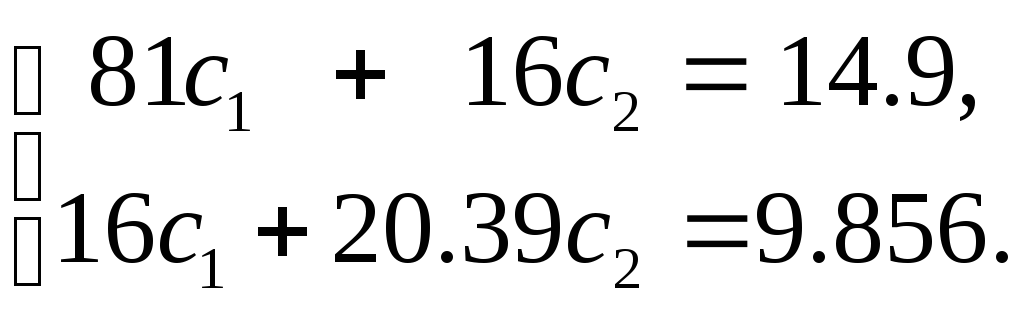
Эта система имеет следующее решение c₁= 0.1047,c₂= 0.4013. Таким образом, аппроксимирующая функция имеет вид

.

Её значения при табличных значения аргумента приведены ниже

x	0.5	1	1.5	2.5	3.5	4
y	0.8550	0.5060	0.4246	0.4223	0.4811	0.5191

С их помощью может быть вычислено значение целевой функции F

которое определяет погрешность аппроксимации

, ,

где норма таблично заданной функции была вычислена следующим образом

.